2020中青杯A题集成电路通道布线数学建模全过程论文及程序

2020中青杯A题集成电路通道布线数学建模

集成电路通道布线

原题再现

  集成电路是利用半导体技术把电子元件集成在一起的具有特定功能的电路，已广泛应用于生产生活的方方面面。随着技术的发展，集成电路内部的元器件数目已达到十亿级别，需要借助专用计算机软件才能完成电路设计与实现，该类软件统称为电子设计自动化（Electronic Design Automation, EDA）工具。
  集成电路设计由多个阶段组成，其中一个重要阶段称为“物理设计”，先将器件摆放在合适的位置，然后用金属线连接器件实现连接关系。其中，后者称为“布线”，它是 EDA 工具需要解决的重要问题。简单而言，假设可用区域由 nxm个方格组成，金属线允许沿着直线或直角（方格）放置，连接指定的方格（引脚）而不引起断路或短路，该过程称为“布线”。由于金属线引入的寄生电阻会影响电路性能，所以需要最小化布线长度。本题重点考虑 “布线”问题中的一个特例：“通道布线”。“通道”是指一个横向的布线区域，此区域的顶部和底部分布着需要连接的方格，需用金属线将相应的引脚连通起来。
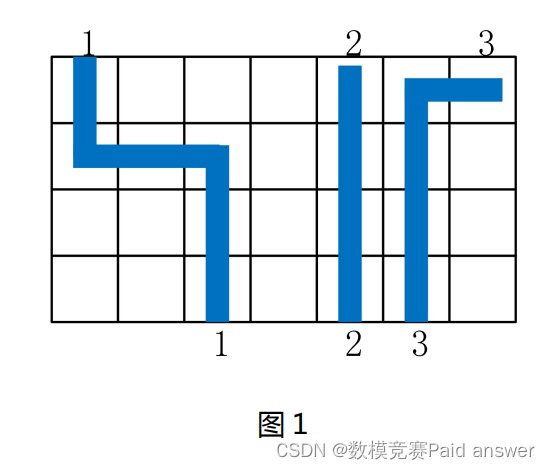
  问题一：假设采用一层金属布线，那么已经布线的方格被锁定，不允许其它线路穿过，否则会形成短路。图 1 所示为采用一层金属的通道布线例子，布线空间为 4x7，空间上下沿的数字分别对应方格的引脚编号，编号相同的引脚需要连接起来。请针对此一层金属的“通道布线”问题完成建模和求解，并回答如下问题：在何种情况下，一层金属通道布线问题无解。

  问题二：可以观察得到，有些测例无法采用一层金属完成布线。实际中，集成电路会采用多个金属层，不同的金属层处在不同的高度，相邻层之间需要用通孔连通，这样不同金属层可共用一个方格而不引起短路。图 2 所示为芯片的剖面图，其中网状填充为金属层，点状填充为通孔。图 3 所示为一个用两层金属的布线示例，其中蓝色为下层金属，黄色为上层金属，红色为通孔。假设一个通孔的电阻等于 5 个方格的导线，请使用最多 3 层金属对“通道布线”重新建模和求解。

  问题三：随着集成电路尺寸缩小，新的通孔制造工艺要求任意两个通孔的间距必须大于等于 2 个格点，请加入此通孔相关的约束后再次求解问题。
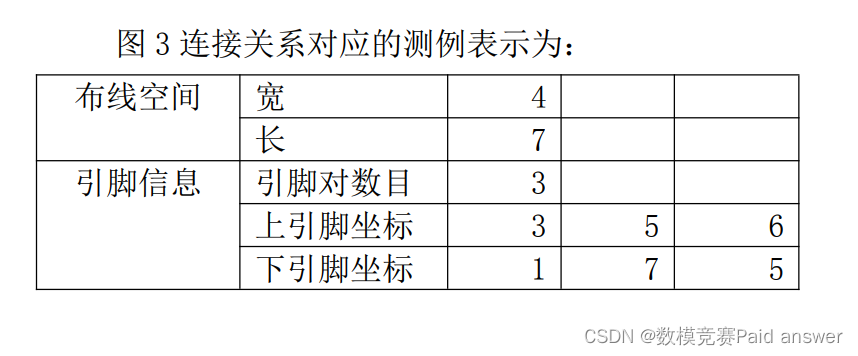
  注：附件为 3 个测试用例，请在上述问题中采用其作为基本测例（可能存在无可行解的情况），鼓励选手增加更为复杂的测试用例，以证明建模和求解的高效性。每个用例一个表格组成，它分别定义了布线空间和引脚的信息。其中，假设“上引脚坐标“和”下引脚坐标“的第 i 个数分别为 ai 和 bi，它们表示需要连接第 1 行的第 ai 个格点与第 n行的第 bi 个格点。

问题分析：

问题一分析

  根据问题一可知，该问题对象为通道布线中的双边双端线网问题，引脚分布于顶边和底边。要求采用一层金属将编号相同的引脚连接起来，每个方格只能布线一次以避免短路。并回答在何种情况下，一层金属通道布线问题无解。
  为了解决该问题，首先需要对题中所给的布线空间建立坐标系，以便于对布线空间中的方格与方格间的路线进行表示，同时建立相关集合以表示各方格与其他方格间的关系，例如是否可以直接用金属线连接连通等，以保证金属线只能沿着水平与垂直方向布线。考虑问题旨在最小化总布线长度，与最短路问题类似，探讨该问题与最短路问题的相似之处与差异点，构建模型，即基于线搜索的并行方法。由此考虑到从基于网格搜索的串行方法，因此还采用了基于改进 A*算法的单层布线算法对问题进行求解。并在模型求解过程中发现了无解时的引脚对的位置关系的规律。

问题二分析

  问题二引入了多层金属层，其间有通孔连。在问题一建立的模型基础上，考虑到多个金属层可以实现不同金属线可共用一个方格而不会引起短路，因此首先考虑将各金属层均映射到最底层，通过交叉点的数量与通道的关系建立二维布线模型，但在模型构建与求解过程中发现一些问题，因此考虑三维空间，增加金属层维度，考虑各项约束，构建了三维布线模型，目标函数中考虑通孔的电阻，对布线方案进行优化。同时也考虑两种不同的角度对问题求解，分别是基于改进最短路的多层三维布线模型（基于线搜索的并行方法）和基于改进遗传算法的多层布线算法（基于网格搜索的串行方法）。

问题三分析

  由问题三可知，要求任意两个通孔的间距必须大于等于 2 个格点，首先对通孔间距进行定义，考虑获取通孔所处的位置，发现所有通孔的位置均能通过中间金属层进行体现，以此为切入点，探讨该金属层上与有通孔的方格距离小于 2 的方格无通孔的约束，以及各种通孔位置关系下的间距的约束，构建了考虑通孔约束的多层三维布线模型并求解。

模型的假设：

  （1）假设每个引脚都在网格中心点上。
  （2）假设当有多个金属层时，上引脚均从底层接入。
  （3）假设金属层厚度足够小，当用三维网络表示方格空间时，任意两通孔上的点间的最短距离表示为这两个通孔间的间距。
  （4）所建立的电路板矩阵能反应电路板实际情况
  （5）假设布线区域的拥堵、时空复杂度对本文布线模型无影响。

模型的建立与求解：

  在集成电路的一层金属布线中，已经布线的方格被锁定，不允许其它线路穿过，否则会形成短路。因此，在避免不同引脚布线相交的同时，要求最大程度最小化布线长度，我们据此建立以下一层金属布线模型。

一层金属布线模型的建立

  为将本问题模型量化进行分析，在此引入工作分解结构（Work BreakdownStructure, WBS）。利用 WBS，将布线目标逐级分解为 n 个不同的带有不同约束条件、不同子目标的条目，将抽象问题直观化。其分解结构如图 5.1 所示。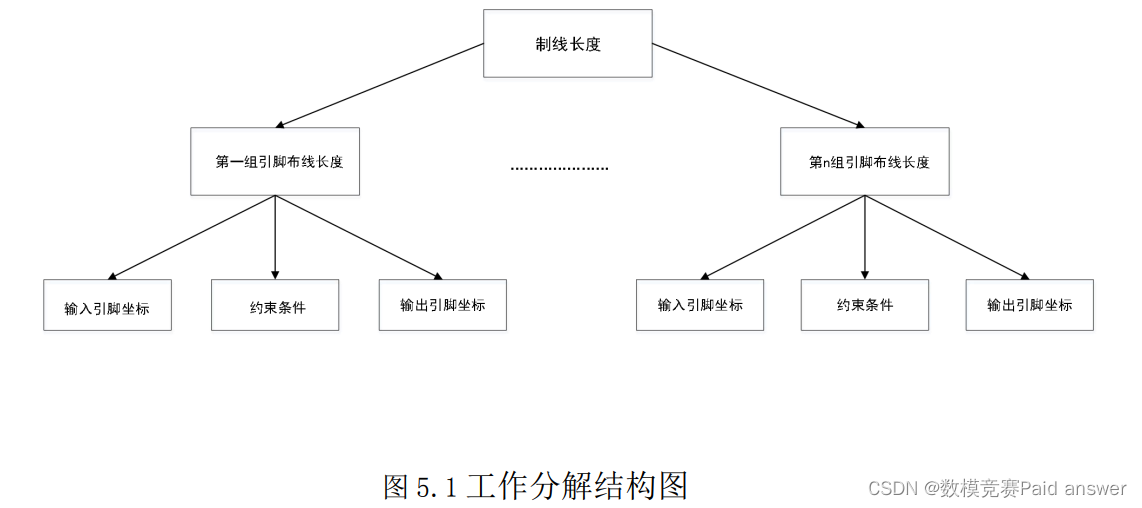
  单条路径最短路模型
  对应单条路径最短路问题，只有一个起点一个终点，即单对 OD，其模型表达式及示例图如下：

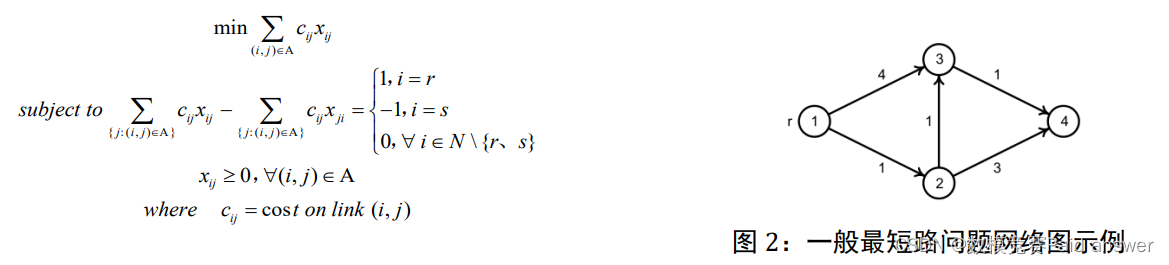
  上述模型寻找从起点r至终点j的最短路径，该路径上的流量为一个单位网络流，模型分别对起点、中间点、终点进出的流量进行限制。对于起点，应当有 1 个单位的网络流流出，无网络流流进，因此进入该点的流量减去进入该点的流量应当等于 1 个单位的网络流。对于终点，应当无流量流进，1 个单位的流量的流出，因此进入该点的流量减去进入该点的流量应当等于-1 个单位的网络流。对于非起点与终点的其他中间点，进入该点的流量应当等于流出该点的容量，因此两者之差等于 0。
  可将本文的问题描述为，对于一个引脚对，从上引脚（起点）开始沿着相邻方格寻找最短路到达下引脚（终点），与最短路问题具有相似性，因此对上述模型进行改进使之适用
于本文需要解决的单层通道布线优化问题。首先将本题的方格映射到寻找最短路的网络中，布线空间中每个方格的中心坐标表示最短路网络中的节点，相邻方格中心的连线（仅包含相邻网格可保证金属线沿着方格放置不会出现断路）代表最短路网络中的链，即连接可相通的节点的弧，由于模型中存在流进与流出方格的流量的概念，所建立的网络为有向网络，相邻方格中心的连线具有方向性。
  与前文单条路径最短路问题不同的是，单层通道布线问题不仅是寻找一个引脚对的最短路问题，在本问题中，每一个引脚对相当于最短路问题中的一个 OD 对，因此单层通道布线问题为同时寻找多个 OD 对的路径问题，同时每两个 OD 路径间无交叉。可将整个问题描述为在前文所建立的二维布线方格网络中，寻找多个引脚对间的路径，在保证引脚对间无交叉的情况下，最小化布线长度。因此，对前文所述的最短路模型进行改进，改进的思路主要包含两个要点：（1）寻找多个引脚对的最短路（总路径最短）；（2）保证每两个引脚对线路间无交叉。基于金属线展开，以相邻方格的连线是否布设金属线为决策变量，以最小化总布线长度为优化目标建立基于改进最短路的 MIP 模型对单层布线问题进行求解。假设对每个 OD 对rs，即每个引脚对分配的网络流为 1 个单位流量，模型构建思路如下（相关符号含义见第四章符号说明）:

问题二模型的建立与求解：

基于改进最短路的多层三维布线模型建立与求解
  本题首先基于第一问中模型，考虑依然基于二维的布线方格，考虑更多的约束建立模型，即对平面中的交叉点数量（用流出该点的总流量和或流入该点的总流量和表示）不超过总金属层数 3 进行限制，在目标函数中用通过交叉点的金属线的数量减 1 表示通道数，用该方法建立了模型并进行了求解（相关代码见附录 3.1）。而后发现在该模型中通道数量与通过交叉点的金属线数量并不存在此关系。因此下文考虑增加金属层维度，建立基于三维网络的布线优化模型。
  由于不同的金属层处在不同的高度，因此布线空间可以看作方格组成的三维空间，因此考虑通过三维坐标重新对问题进行建模，金属线间通过不同金属层实现不短路，即可以看作在三维空间中不同金属线不会相交，否则出现短路情况。从三维的角度本题考虑了两种情况：（1）所有的金属线均需要从底层下引脚处连出；（2）金属线可以从任意层的下引脚处连出。下面针对这两种情况分别建模。

  依然调用 Gurobi 对上述模型进行求解，采用的方法是对偶单纯形法。利用本模型对于测例 1、测例 2 和测例 3 分别进行测试，发现采用多层金属层时，测例 1、测例 2 和测例 3依然调用 Gurobi 对上述模型进行求解，采用的方法是对偶单纯形法。利用本模型对于测例 1、测例 2 和测例 3 分别进行测试，发现采用多层金属层时，测例 1、测例 2 和测例 3

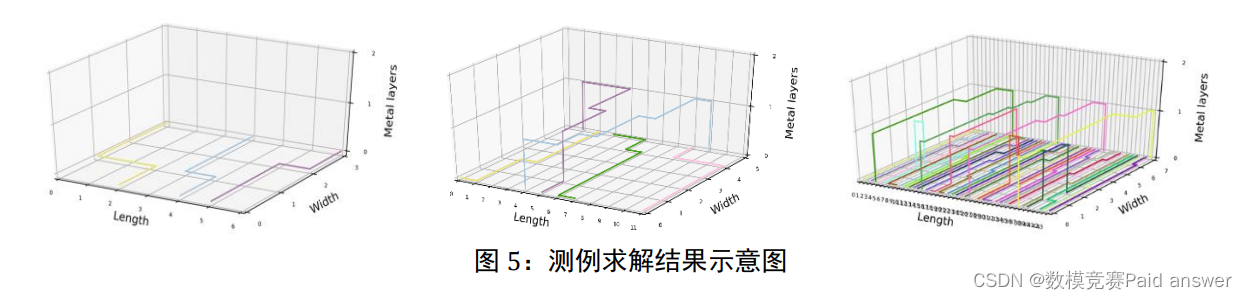
问题三模型的建立与求解：

  针对问题三，在问题二下引脚均从底层连出的假设的基础上增加了任意两个通孔的间距必须大于等于 2 个格点的约束，首先对通孔间距进行定义，考虑获取通孔所处的位置，发现所有通孔的位置均能通过中间金属层进行体现，以此为切入点，探讨该金属层上与有通孔方格的距离小于 2 的方格无通孔的约束，构建模型进行求解，发现该约束对共z轴通孔无约束，此时，三个测例都有可行解，当针对该情形通过探讨变量间的关系增加了相关约束，结果表明只有测例 1 有解，其他测例无解，也说明了本文相关假设稍有严格。

以上内容仅为论文中部分内容(仅供参考)，详情见最下方。

论文缩略图

程序代码

from gurobipy import * 
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
info = pd.read_excel("测例 1.xlsx", "Sheet1",header = None,skiprows=None)
info = info.values
length = info[1][2]
width = info[0][2]
paths_num = info[2][2]
starts = []
ends = []
starts_path = []
ends_path = []
for path in range(paths_num): #该 width 和 0 的位置
 start = (info[3][path+2]-1, 0)
 end = (info[4][path+2]-1, width-1)
 start_path = (path,info[3][path+2]-1, 0)
 end_path = (path,info[4][path+2]-1, width-1)
 
 starts.append(start)
 ends.append(end)
 starts_path.append(start_path)
 ends_path.append(end_path)
x_index = {
    
    }
for path in range(paths_num):
 for i in range(length):
 for j in range(width):
 if i-1>=0:
 x_index[path,i,j,i-1,j] = 0
 if i+1<= length-1:
 x_index[path,i,j,i+1,j] = 0
 if j-1>=0:
x_index[path,i,j,i,j-1] = 0
 if j+1<= width-1:
 x_index[path,i,j,i,j+1] = 0
try: 
 mo = Model("MIP")
 
 #x = mo.addVars(point1_index.keys(),obj=1, vtype=GRB.BINARY, name='x') 
 x = mo.addVars(x_index.keys(), vtype=GRB.BINARY, name='x')
 obj = 0
 for i in x_index.keys():
 obj = obj + x[i]
 mo.setObjective(obj, GRB.MINIMIZE)
 
 for i in range(length):
 for j in range(width):
 for path in range(paths_num):
 if (path,i,j) in starts_path:
 mo.addConstr((x.sum(path,i,j,'*','*') == 1),"1")
 #mo.addConstr((x.sum(path,'*','*',i,j) == 0),"2")
 else:
 if (path,i,j) in ends_path:
 #mo.addConstr((x.sum(path,i,j,'*','*') == 0),"3")
 mo.addConstr((x.sum(path,'*','*',i,j) == 1),"4")
 else: #包含其他 path 经过起终点
 mo.addConstr((x.sum(path,i,j,'*','*') - x.sum(path,'*','*',i,j) == 
0),"5")
 for i in range(length):
 for j in range(width):
 if (i,j) in starts:
 mo.addConstr((x.sum("*",i,j,'*','*') == 1),"3")
 mo.addConstr((x.sum("*",'*','*',i,j) == 0),"3")
 else:
 if (i,j) in ends:
 mo.addConstr((x.sum("*",i,j,'*','*') == 0),"3")
 mo.addConstr((x.sum("*",'*','*',i,j) == 1),"3") 
 else:
 mo.addConstr((x.sum('*',i,j,'*','*') <= 1),"6")
 mo.addConstr((x.sum('*','*','*',i,j) <= 1),"7)
 ''' 
 for i in range(length):
 for j in range(width):
 for path in range(paths_num):
 if (path,i,j) in starts_path:
 mo.addConstr((x.sum(path,i,j,'*','*') == 1),"1")
 #mo.addConstr((x.sum(path,'*','*',i,j) == 0),"2")
 else:
 if (path,i,j) in ends_path:
 #mo.addConstr((x.sum(path,i,j,'*','*') == 0),"3")
 mo.addConstr((x.sum(path,'*','*',i,j) == 1),"4")
 for i in range(length):
 for j in range(width):
 if (i,j) in starts:
 mo.addConstr((x.sum("*",i,j,'*','*') == 1),"3")
 mo.addConstr((x.sum("*",'*','*',i,j) == 0),"3")
 else:
 if (i,j) in ends:
 mo.addConstr((x.sum("*",i,j,'*','*') == 0),"3")
 mo.addConstr((x.sum("*",'*','*',i,j) == 1),"3") 
 else:
 mo.addConstr((x.sum('*',i,j,'*','*') <= 1),"6")
 mo.addConstr((x.sum('*','*','*',i,j) <= 1),"7")
 for path in range(paths_num):
 if (i,j) not in starts:
 if (i,j) not in ends:
 mo.addConstr((x.sum(path,i,j,'*','*') - x.sum(path,'*','*',i,j) == 
0),"5")
 '''
 mo.optimize()
 bestX = {
    
    }
 bestX_1 = []
 for i in x_index.keys():
 bestX[i] = x[i].x
 if bestX[i] ==1:
 print(i)
 bestX_1.append(i)
 #print(bestX.keys())
 #plt.title('a')
 colors = ['r','g','b', 'c', 'm', 'y']
 for arc in bestX_1:
 for path in range(paths_num):
 if arc[0] == path:
 #color = np.zeros((100,100))*(path+1)
 plt.plot([arc[1],arc[3]],[arc[2],arc[4]],c=colors[arc[0]])
 #plt.legend()
 plt.axis([-0.1,length-0.9,0,width-1])
 my_x_ticks = np.arange(0,length, 1)
 my_y_ticks = np.arange(0,width, 1)
 plt.xticks(my_x_ticks)
 plt.yticks(my_y_ticks)
 plt.xlabel('Length')
 plt.ylabel('Width')
 plt.savefig('P1_1', dpi=300, bbox_inches = 'tight')
 plt.show()
 
except GurobiError as exception:
 print('Error code ' + str(exception.errno) + ": " + str(exception))