起飞 —— 算法期末考前必看常见例题总结

1. 分治算法求最大值和最小值

核心思想：先设立边界条件，也就是能直接看出来结果的最小的子问题，即数组中只有一个元素和只有两个元素的时候的情况。然后递归不断将问题二分求解。

算法MaxMin(A)
输入：数组A[i...j]
输出：数组A[i...j]中的max和min
if j-i+1 = 1  Then  输出A[i],A[i]，算法结束
if j-i+1 = 2  Then
    if A[i] < A[j]  Then  输出A[i], A[j], 算法结束
    else  Then  输出A[j], A[i], 算法结束
k ⬅ (j-i+1) / 2
m1, M1 ⬅ MaxMin(A[i : k]);
m2, M2 ⬅ MaxMin(A[k + 1 : j]);
m ⬅ max(m1, m2)
M ⬅ min(M1, M2)
输出m, M

注：求第 k 大数的一般性问题有一定难度，如需理解，请参考博文：https://blog.csdn.net/m0_51339444/article/details/124360978

2. 快速排序

核心思想：采用分治思想，递归地不断地将整个数组一分为二，每次将子数组的首元素作为中轴，找到该元素应在的位置，以此位置作为分割点，可见，分割点越接近中间位置，算法效率越高。

算法 Partition(A[l...r])
// 以第一个元素为中轴，划分数组
// 输出：A[l...r]的一个分区，返回划分点位置
p ⬅ A[l];
i ⬅ l;  j ⬅ r;
repeat
     repeat  i ⬅ i + 1  until  A[i] ≥ p
     repear  j ⬅ j + 1  until  A[j] ≤ p
     swap(A[i], A[j]);
until i ≥ j
swap(A[i], A[j])   // i ≥ j, 撤销最后一次交换
swap(A[l], A[j])
return j;

算法 QuickSort(A[l...r])
// 输入：数组A[0...n-1]的子数组
// 输出：非降序的子数组A[l...r]
if(l < r){
    
    
     s ⬅ Partition(A[l...r]);
     QuickSort(A[l...s-1]);
     QuickSort(A[s...r]);
}

3. 折半查找

核心思想：折半查找要求数组是有序的，每次将查找键和中间位置的元素比较，小于则在左半区查找，大于则在右半区查找

算法 BinarySearch(A[0...n-1], k)
// 非递归折半查找
// 输入：升序数组A[0...n-1]和查找键K
// 输出：找到键k, 返回K所在下标，否则返回-1
l ⬅ 0; r ⬅ n - 1;
while(l ≤ r)  do{
    
    
     m ⬅ (int)(l + r) / 2;
     if (K = A[m])  return m;
     else if (K < A[m])  r ⬅ m - 1;
     else l ⬅ m + 1;
}
return -1;

4. 找第k大数的一般性问题

核心思想：5个数一组，先找到每组的中位数，然后找到各组中位数的中位数，找到所有比该数小的所有元素，或者比该数大的所有元素，然后递归上述步骤。

5. 动态规划求解矩阵连乘问题

核心思想：先设定边界条件，m[i, i] 不需要运算，即运算次数为0，然后自底向上利用规划方程求解规模更大的子问题，规划方程如下：x ⬅ m[i, k] + m[k + 1, j] + P[i - 1] * P[k] * P[j];

算法：矩阵连乘问题
// 输入：<A1, A2, ..., An>, Ai是pi-1 * pi矩阵
// 输出：计算A1 * A2 *...* An的代价最少的计算次序
if  i = j  m[i,j] ⬅ 0;
m ⬅ ∞;
for  k = i  to  j-1  do{
    
    
  x ⬅ m[i, k] + m[k + 1, j] + P[i - 1] * P[k] * P[j];
  if x < m   
     m = x;
} 
m[i,j] ⬅ m;

注：上面的伪代码仅仅能求出结果，但是无法返回最小计算次数对应的分割方案。如果题目需要得到分割方法，则需要再构造一个s[i, j] 数组，里面存储将其直接分割的位置。对于此问题的详细题解请参考之前的blog : https://blog.csdn.net/m0_51339444/article/details/123970382

6. DP求解LCS最长公共子序列问题

//
// Created by 23011 on 4/4/2022.
//

//最长公共子序列
#include<cstdio>
#include <iostream>
#include<string>
#include<cstring>
#define MAX 1001
using namespace std;
int dp[MAX][MAX];
int main()
{
    
    
    int n;
    scanf("%d", &n);
    while(n--)
    {
    
    
        string a,b;
        cin >> a >> b;
        memset(dp,0,sizeof(dp));
        int len_a = a.size(), len_b = b.size();
        for(int i = 0;i < len_a; i++)
        {
    
    
            for(int j = 0; j < len_b; j++)
            {
    
    
                if(a.at(i) == b.at(j))
                    dp[i + 1][j + 1] = dp[i][j] + 1;
                else
                    dp[i + 1][j + 1] = max(dp[i + 1][j], dp[i][j + 1]);
            }
        }
        printf("%d\n",dp[len_a][len_b]);
        a.clear();
        b.clear();
    }
    return 0;
}

7. DP求解二项式系数

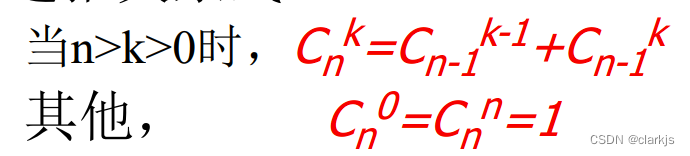
算法 Binomial(n,k)
//用动态规划算法计算C(n,k)
//输入：一对非负整数n ≥ k ≥ 0
//输出：C(n,k)的值
for  i = 0  to  n  do
     for  j = 0  to  min(i,k)  do
          if j=0 || j=i   Then  C[i,j] ⬅ 1;
          else 
               C[i, j] ⬅ C[i-1, j-1] + C[i-1,j];
Return C[n,k];

8. DP求多段图问题

这个问题要求我们求解从源点 s 到汇点 t 的最短路径，下面将介绍两种方法的动态规划，向前算法和向后算法，向前算法就是从距离汇点最近的一列点开始，根据规划方程逐步向源点推进；向后算法则相反，由源点向汇点计算。

（1）向前算法（自底向上）（常用）

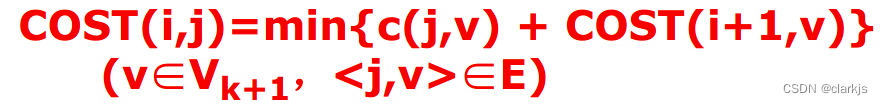
（2）向后算法（自顶向下）

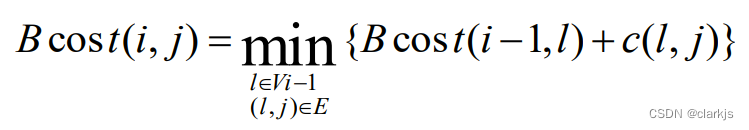
9. Floyd算法（DP）

核心思想：先将距离矩阵初始化（无跳板），能直接达到则记录距离值，不能直接达到则即为∞，自己到自己的距离即为0。然后从小到大遍历每个点，以该点作为跳板观察距离矩阵中是否有元素可以更新（更小），这个过程中，需要遍历距离矩阵中的每个点，即二重循环遍历每个顶点。因此Floyd算法的时间复杂度是O(N^3^)

for (k = 0; k < G.vexnum; k++)
    {
    
    
        for (i = 0; i < G.vexnum; i++)
        {
    
    
            for (j = 0; j < G.vexnum; j++)
            {
    
    
                // 如果经过下标为k顶点路径比原两点间路径更短，则更新dist[i][j]和path[i][j]
                tmp = (dist[i][k]==INF || dist[k][j]==INF) ? INF : (dist[i][k] + dist[k][j]);
                if (dist[i][j] > tmp)
                {
    
    
                    // "i到j最短路径"对应的值设，为更小的一个(即经过k)
                    dist[i][j] = tmp;
                    // "i到j最短路径"对应的路径，经过k
                    path[i][j] = path[i][k];
                }
            }
        }
    }

详细过程请参考blog :https://blog.csdn.net/m0_51339444/article/details/123904762

10. 计算有向图的传递闭包（DP）

大家可能对于这个问题不是很熟悉，这里介绍得详细一些：此问题要求我们计算有向图的传递闭包，也就是要求我们得出哪些点之间是可达的，在矩阵中记为1，哪些点是不可达的，记为0。这个问题我们使用的是Warshall算法，思路与Floyd算法非常类似，先初始化矩阵，即无中间跳板，直接可达记为1，非直接可达记为0（通过下面例子更容易理解）。然后按照a,b,c,d的顺序增加跳板，看看哪些点对之间变成了可达的，即更新为1. 规划方程如下：

我们尝试理解一下这个规划方程，以 k 为跳板即为从 i 到 j ，必须以 k 为跳板，看看能不能把0变成1，也就是说，从 i 到 j 且以 k 为跳板，即这条路径一定是【i, k】和【k, j】

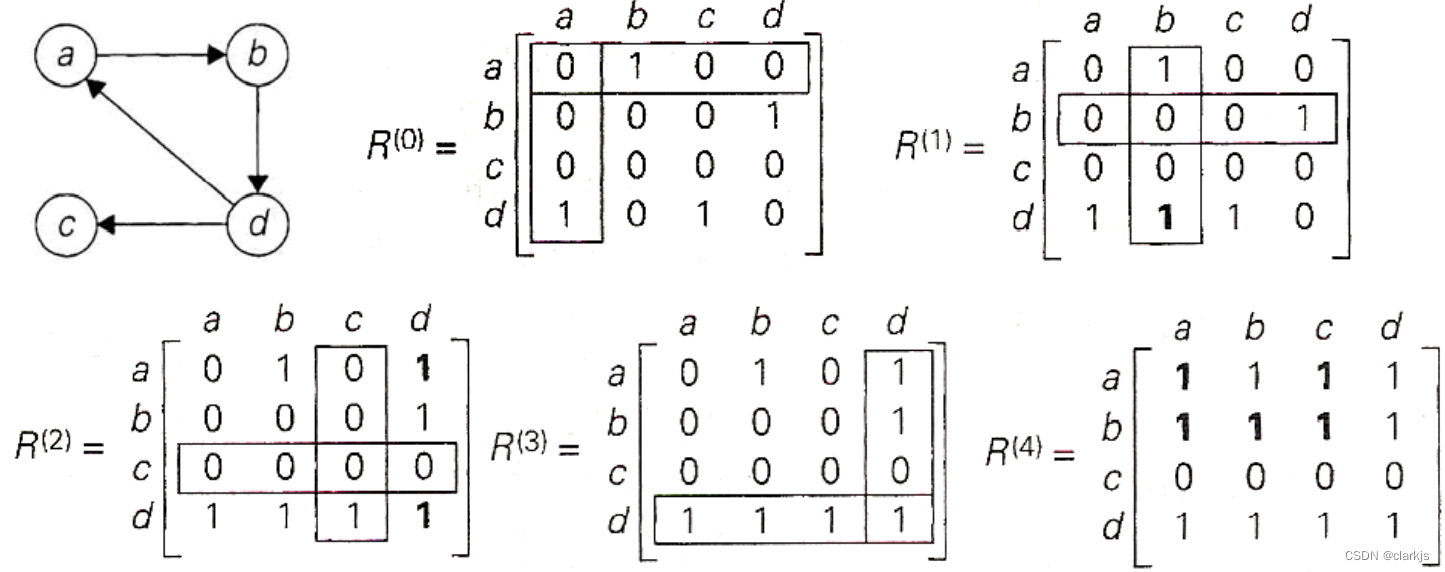
算法 Warshall(A[1..n,1..n])
//实现计算传递闭包的Warshall算法
//输入：包括n个节点有向图的邻接矩阵
//输出：该有向图的传递闭包
R(0) ⬅ A
for  k = 1  to  n  do
     for  i = 1  to  n  do
          for  j = 1  to  n  do
               R(k)[i,j] ⬅ R(k-1)[i,j] or (R(k-1)[i,k] and R(k-1)[k,j])
return R(n)

11. 最优二叉查找树

在介绍此问题之前，我们先回忆以下二叉查找树，左子树的节点都小于根节点，右子树的节点都大于根节点，这样只需将待查找元素和根节点比较一次，即可直接剪枝左子树或者右子树。看起来效率很高，但实际上不同的构造方法的效率差异是极大的，我们看下面的例子：

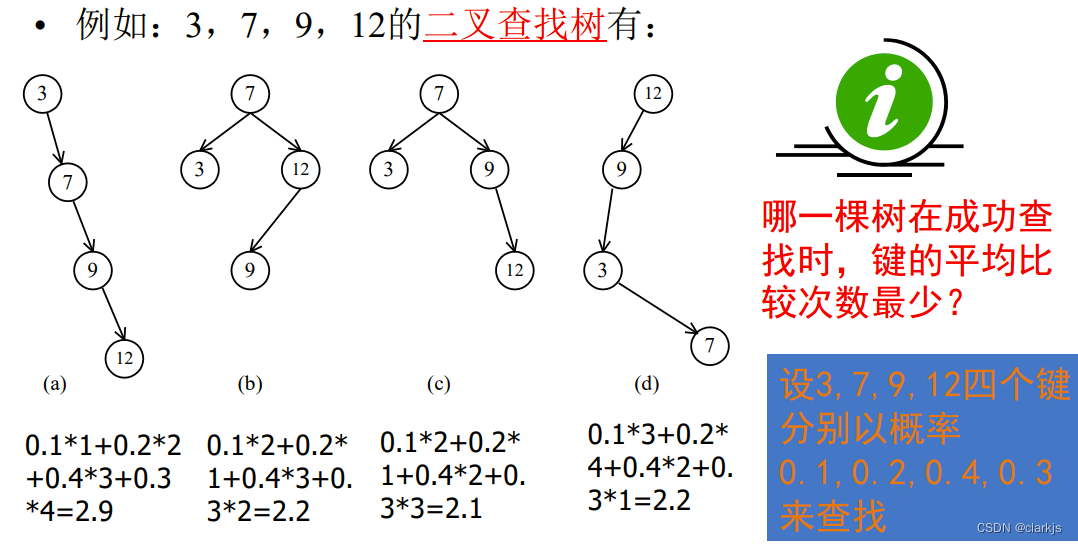
可见，不同的建树方式的效率差异很显著，因此，我们引入了最优二叉查找树，目的就是构建一棵平均比较次数最小的二叉树。规划方程如下：

实际上不难理解，两棵子树【i, k - 1】和【k + 1, j】已构建好，当我们加入根节点 k 后，两棵子树分别为 a_k的左右子树，即每个节点的深度都 +1，包括 k 本身（从0变成1），因此后面加上了所有节点出现的概率和。示例如下：

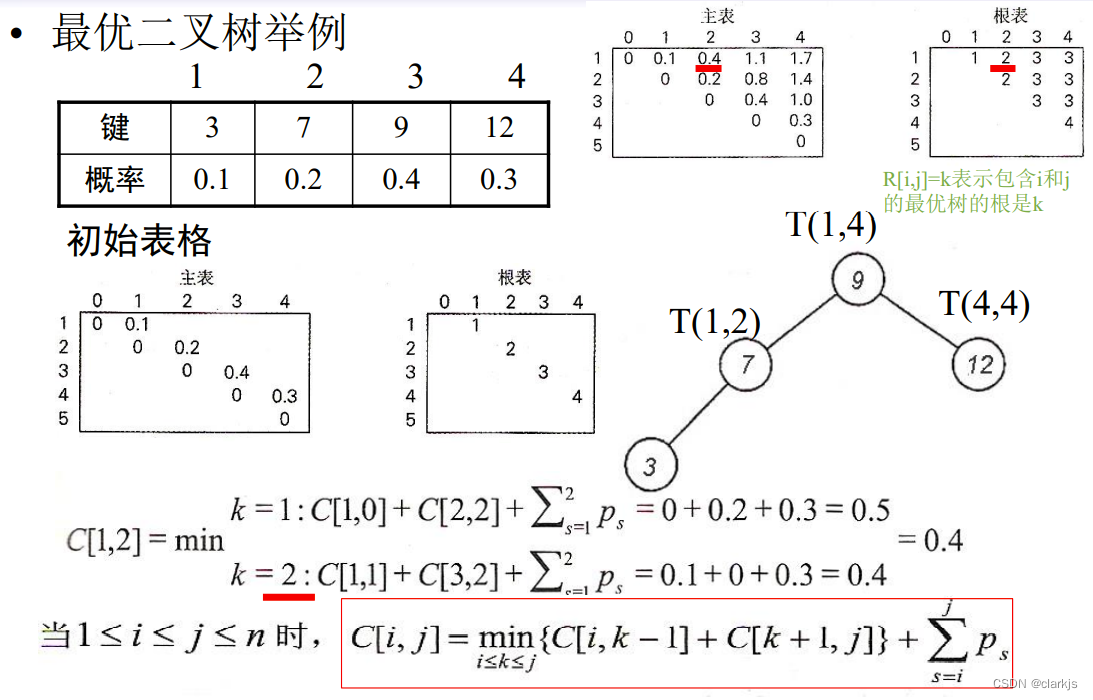
算法 OptimalBST(P[1..n])
//用动态规划算法求解最优二叉树
//输入：一个n个键的有序列表的查找概率数组
//输出：成功查找平均比较次数，根表R
for(i ⬅ 1; i <= n; i++){
    
    
     C[i, i-1] ⬅ 0; C[i,i] ⬅ i; R[i,i] ⬅ i;
}
C[n+1,n] ⬅ 0;
for(d ⬅ 1; d < n; d++)
     for(i ⬅ 1; i <= n - d; i++){
    
    
          j ⬅ i + d; minval ⬅ ∞;
          for(k ⬅ i; k <= j; k++)
               if(C[i, k - 1] + C[k + 1, j] < minval){
    
    
                    minval ⬅ C[i, k - 1] + C[k + 1, j]; kmin ⬅ k;
               }
          R[i,j] ⬅ k; sum ⬅ P[i];
          for(s ⬅ i + 1; s <= j; s++)
               sum ⬅ sum + P[s];
          C[i, j] ⬅ minval+sum;
     }
return C[1, n], R;

12. 背包问题

在这里不作详细的解释，详细的背包问题请参考blog: https://blog.csdn.net/m0_51339444/article/details/123934681，但是有一点务必重新总结一下：0-1背包和完全背包都不能用贪心，因为得不到最优解，而依赖背包（物品可拆，例如沙子）则可以使用贪心算法，但是要予以证明

13. 货担郎问题（DP）

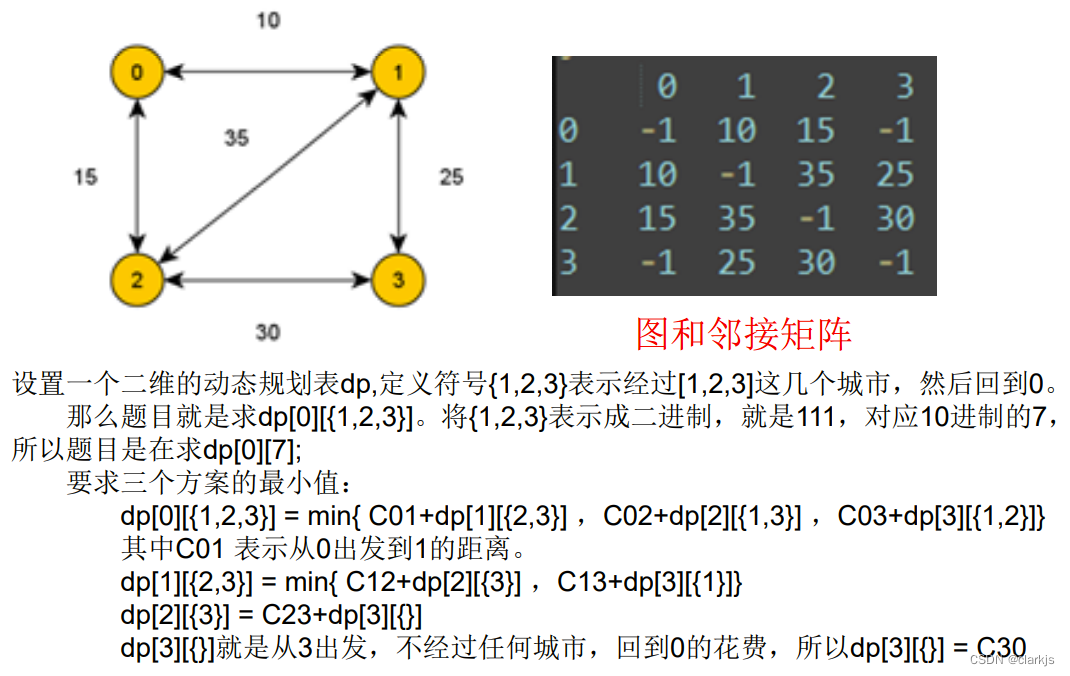
可见，使用DP求解此问题可以降低时间复杂度，但是空间复杂度却会大大增加，即以空间换时间。
详细内容及代码可以考虑参考blog:https://blog.csdn.net/wu_tongtong/article/details/78172856

14. 电路布线问题（DP）

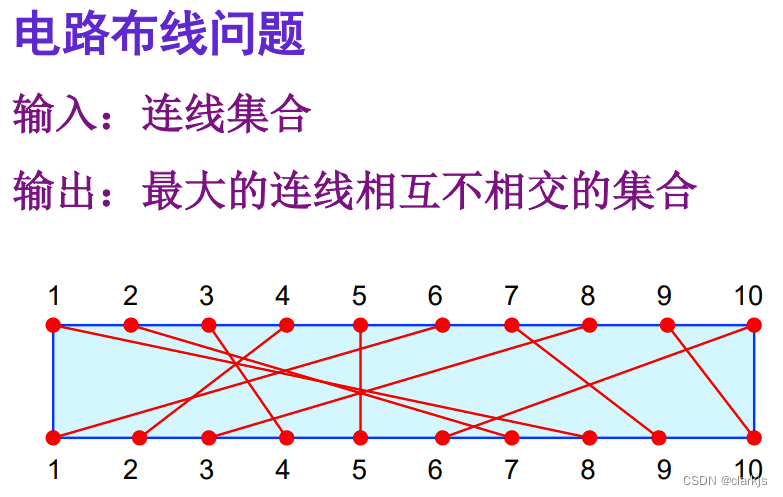
这个问题看起来很新颖，实际上，仔细思考一下就可以转换成我们常见的形式，如下图所示：

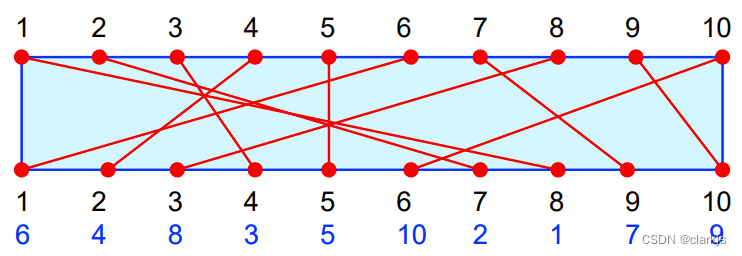
上图中我们把与下面线路相连的数字都写在最下面，我们想一下，假如下面的 1 与 上面的 i 相连，则为了保证不相交， 下面的2 必定和 >i 的号码相连，即我们将问题转化为，求上图中蓝色的一串数字中的最长升序子序列。解决这个问题请参考blog:https://blog.csdn.net/Junyi727/article/details/117410657，不过在这个blog里博主存在一个疑问：求以 i 为结尾的最长升序子序列时（求dp[i]）, 第二重循环的目的应该是找到上一个比 i 小的元素，那应该从 i 往前遍历更快啊，为什么从 0~i 顺序遍历啊？ （目的是找 0~i中最后一个小于 i 号元素的元素）

15. 优化三角剖分问题（DP）

待定

16. 最大连续子序列和

参考博主之前的博文：https://blog.csdn.net/m0_51339444/article/details/123769968

17. （贪心算法）活动安排问题

该问题是有一个场地，已知多个活动的开始时间和结束时间，请你进行场地安排，尽可能使更多的活动被安排。
这个问题使用贪心算法进行求解，之前我们说过，贪心算法的方案不唯一，而且不一定能找到最优解，比如我们可以按活动持续时间长短排序，有短到长安排活动；或者根据活动开始时间由前向后安排活动。这都属于贪心算法，即满足当前最优的情况。但是，我们需要得到的最优解，即安排最多的活动，这就需要我们进一步证明了。
核心思想：讲各个活动按照结束时间由前向后排序，每次在保证不和之前活动冲突的前提下选取最先结束的活动，这就设计好了贪心算法。然后需要给予证明，从贪心选择性和优化子结构两个方面进行证明，以保证我们可以得到最优解。

18. （贪心算法）最小生成树

（1）Prim

核心思想：（加点法）将所有顶点分割为两个集合，收录和待收录，每次将距离收录集合最近的一条边对应的待收录点收录（贪心：每次选最近），然后更新待收录点与已收录点的最短距离（skill : 因为更新的点肯定是与V邻接的，非邻接的肯定不会被更新，因此只需要遍历V的邻接点W即可）。最后如果已收录的顶点个数小于图的总顶点个数，说明最小生成树不存在。

void Prim()
{
    
    
     MST = {
    
    s};
     while(1){
    
    
          V = 未收录顶点中dist最小的节点；
          if(这样的V不存在)      // 说明不是连通网即不连通
               break;
          // dist数组表示未收录节点距离已收录的树中某节点的最小值，因此，将节点V收录后即dist[V]为0
          将V收录进MST : dist[V] = 0; 
          // 逐个遍历刚收录进去的V点的所有邻接点，检验是否有顶点因为V的收录而使其距离已收录集合的最小距离变小，
          // 如有，则更新，并记录该点到已收录集合的最小距离是该点到V点
          for(V的每个邻接点W)
               if(dist[W] != 0) // W未被收录
                    if(C(V,W) < dist[W]){
    
    
                         dist[W] = C(V,W);
                         parent[W] = V;
                    }
     }
     if(MST中收录的顶点数小于V个)
          ERROR("生成树不存在");
}

（2）Kruskal

核心思想：（加边法）每次从所有边中找到权值最小的边并收录进去，并检查是否构成回路，如果构成回路，则彻底无视这条边（因为之后也肯定不会收录）。最后如果已收录的顶点个数小于图的总顶点个数，说明最小生成树不存在。

void Kruskal (Graph G)
{
    
    
     MST = {
    
     };
     while(MST中不到|V|条边 && E中还有边){
    
    
          从E中取一条最小的边E(V,W); //最小堆OR斐波那契堆
          将E(V,W)从E中删除;
          if(E(V,W)不在MST中构成回路)  // 并查集
               将E(V,W)加入MST;
          else 
               彻底无视E(V,W);
     }
     if(MST中不到|V|条边)
          ERROR("生成树不存在");
}

19. （贪心）哈夫曼编码

核心思想：采用堆的方式，每次选择两个概率最小的元素，将相加后的概率扔进堆中，不断重复此操作，目的是尽可能将概率小的置于树的更深的位置（编码较长），出现概率大的元素靠近根（编码短），这样可以使平均码长最小。

证明：
（1）在平均码长最小的编码方案这个最优解中，编码最长的肯定是堆中概率最小的元素
【反证法】如果不是，则将编码最长的元素的编码与出现概率最小的元素的编码互换，平均码长肯定比原优化解更短，证毕。
（2）将出现概率最小的元素删除，得到的子问题中，编码最长的肯定是堆中概率最小的元素
证明方法同上
（3）根据以上两条引理，我们可以证明贪心选择性和最优子结构，即每次都从堆中选择两个概率最小的元素由叶子向树根反向进行建树。（补充：因为插入元素时会将之前的元素（2个）压向更深的一层，即使得总码长的增加量为这两个元素的概率之和，因此每次取元素后，需要将这两个元素出现概率之和压入堆中）

Huffman(C, F)
{
    
    
	n <- |C|;
	Q <- C;
	FOR i <- 1 To n-1 Do
		z <- Allocate-Node();
		// 使用二叉堆找到出现频率最小的节点并置为左孩子lch
		x <- left[z] <- Extract-MIN(Q);
		// 使用二叉堆找到出现频率次小的节点并置为右孩子rch 
		y <- right[z] <- Extract-MIN(Q);
		f(z) <- f(x) + f(y);
		Insert(Q, z);
	Return;
}

20. （贪心）多机调度问题

核心思想：（1）如果机器数量 n 小于等于任务数量 m ，则只需一个任务安排一台机器即可 （2）若 机器数量 n 大于任务数量 m，则先把前 n 长的任务各安排一台机器，然后依次将剩余任务中最长的任务安排到最先结束的机器中。样例示意图如下：

补充：多机调度问题是NPC问题，因此是几乎找不到最优解的，贪心算法只是找到可行解（近似最优解），因此不需要给予证明。

21. （回溯法） 最优装载问题

问题描述如下：

核心思想：只需要保证c1集装箱尽最大可能装满，剩余货物直接进入c2集装箱即为最优解，因为如果c1尽可能装满了剩下货物都装不进c2，说明此题无解。我们采用回溯的思想，深度优先搜索并实时剪枝（按顺序（重 --> 轻）考虑，只要装入该货物超重，则直接剪枝，将该货物标记为0，表示不装入，该货物标记为1的子树全部剪掉，因为满足多米诺性质）。
缺点：回溯不完全，还可以设计代价函数，如将剩余所有货物都装载，得到的解仍然小于目前寻得的最优解，则直接剪枝，这样会再次缩小搜索空间。

虽然理论上时间复杂度是O(2ⁿ)，但实际计算时肯定远小于此值，剪枝会剪掉很多一般，2ⁿ其实是蛮力法的效率。

算法 Loading(W, c1)
// 输入：货物重量W = <w1...wn>，以及两个集装箱的最大载重量
// 输出：使得1号集装箱尽可能装满的装载方案
Sort(W);
B ⬅ c1; best ⬅ c1; i ⬅ 1;  // B为c1箱当前空隙，best为最小空隙
while  i ≤ n  do
     if  装入i后重量不超过c1
     then  B ⬅ B - wi;  x[i] ⬅ 1;  i = i + 1;
     else  x[i] ⬅ 0;  i = i + 1;
if  B < best  then 记录解;  best ⬅ B;
BackTrack (i);  // 回溯
if (i = 1)  then  return 最优解
else goto 3	   // 从while开始执行


算法 Backtrack(i)
while  i > 1  and  x[i] = 0  do
     i ⬅ i - 1;
if (x[i] = 1)
then  x[i] ⬅ 0;
      B ⬅ B + wi;
      i ⬅ i + 1;

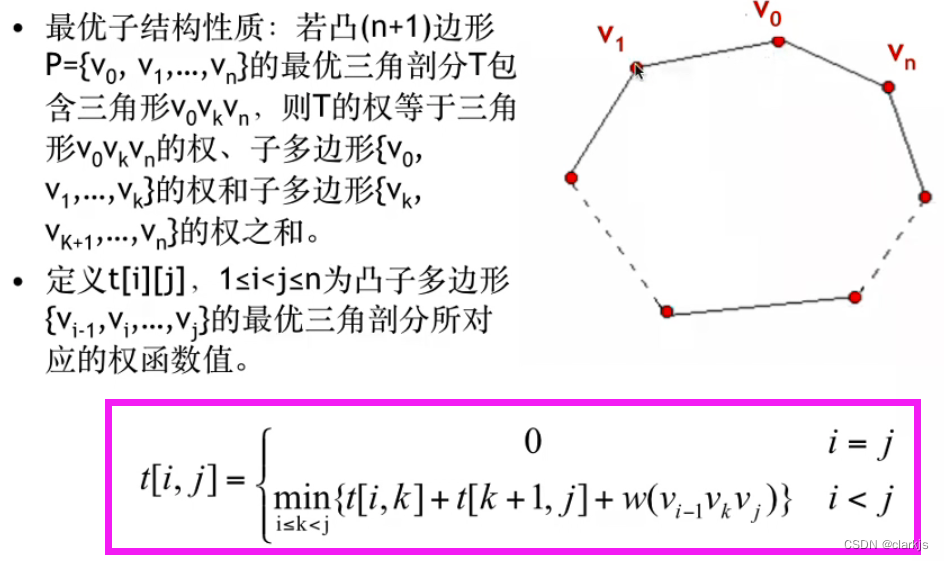
22. （DP）凸多边形优化三角剖分

这个问题稍微冷门一些，因此在这里我将详细地介绍。先来看一下凸多边形的定义：（通俗地来讲，就是在多边形中任取两个点并连线，如果均在多边形内，则该多边形是凸多边形）。


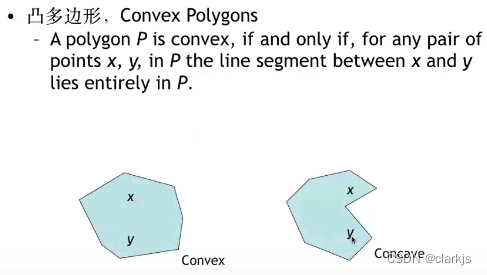
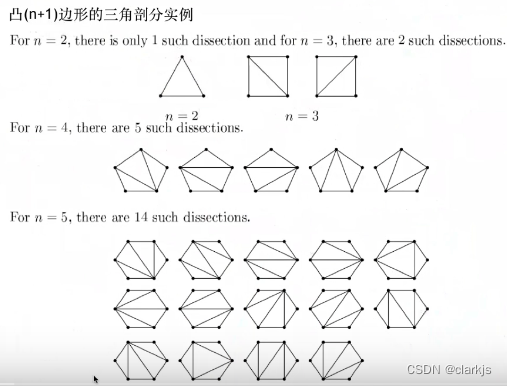
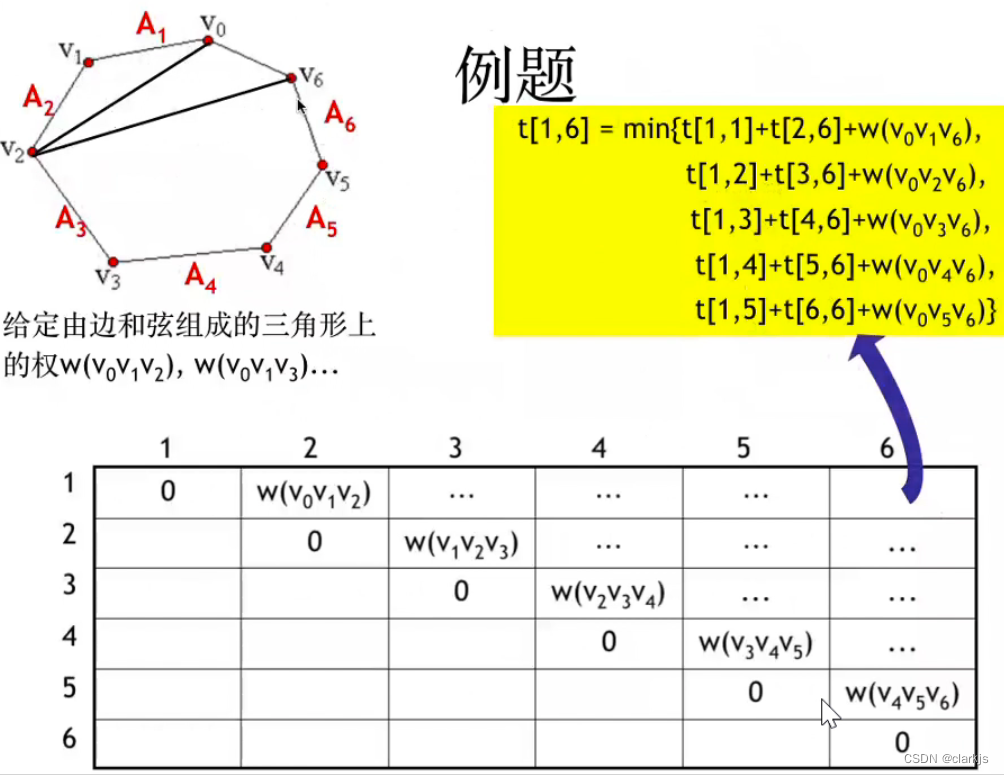
我们的目的是解决优化三角剖分问题，即将凸多边形（N条边）通过N-3条弦（不相邻顶点的连线）划分为N-2个小三角形，每个三角形的代价为三个顶点权值的乘积，整个划分的代价为各个小三角形划分的代价之和。我们要求解N边的凸多边形各个三角剖分中代价最小的剖分，可以使用蛮力法，即遍历所有情况，求出其中的最优解，如上图所示：3边形的三角剖分只有1种，4变形的三角剖分有2种，5边形有5种，6边形14种。但是，蛮力法复杂度显然过高，因此今天我们将主要介绍动态规划算法。
首先，回忆一下矩阵连乘问题：https://blog.csdn.net/m0_51339444/article/details/123970382,N个矩阵，输入为N+1个，而三角剖分问题其实和矩阵连乘问题是等价的，N边形的凸多边形有N条边和N+1个点及其权值，而三角形的代价为三个权值相乘，即和两个矩阵相乘需 i * j * k相对应，可以根据下面的两张图再理解一下：


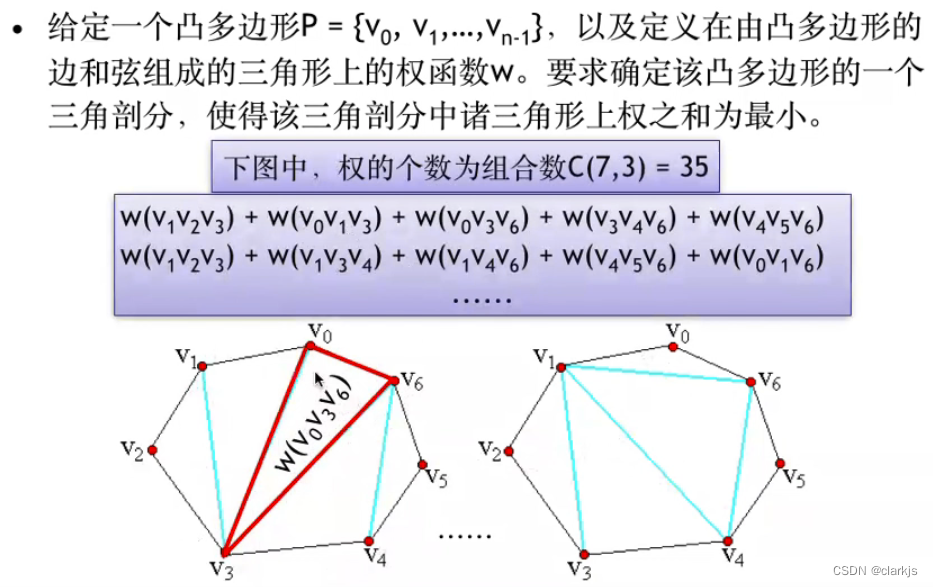
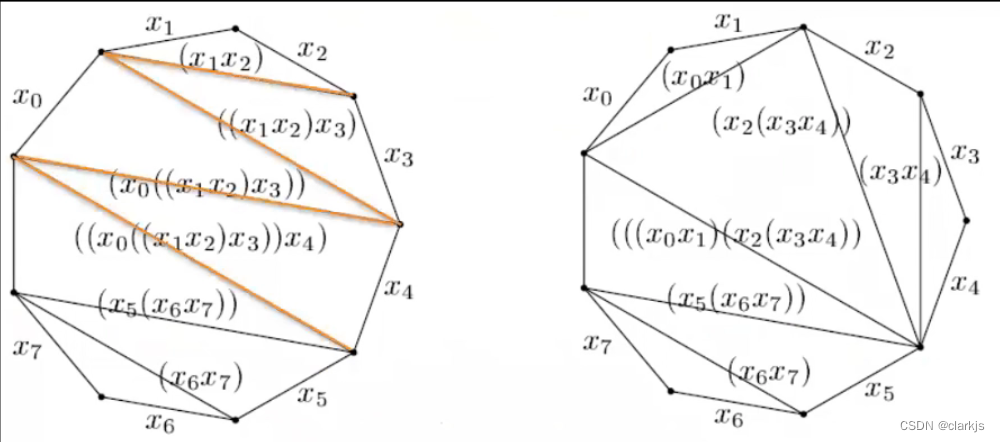
我们刚才已经明白了，优化三角剖分问题其实就是矩阵连乘问题，可以得到规划方程如下：