零知识证明系列之三——入门zkSNARK

前文回顾

回顾一下一套完善的零知识证明体系需要以下的条件：

（1）完备性（Completeness）如果证明方和验证方都是诚实的，并遵循证明过程的每一步，进行正确的计算，那么这个证明一定是成功的，验证方一定能够接受证明方。

（2）合理性（Soundness）没有人能够假冒证明方，使这个证明成功。

（3）零知识性（Zero-knowledge）证明过程执行完之后，验证方只获得了“证明方拥有这个知识”这条信息，而没有获得关于这个知识本身的任何一点信息。

接下来就是我们的重头戏zksanrk了。

预备知识

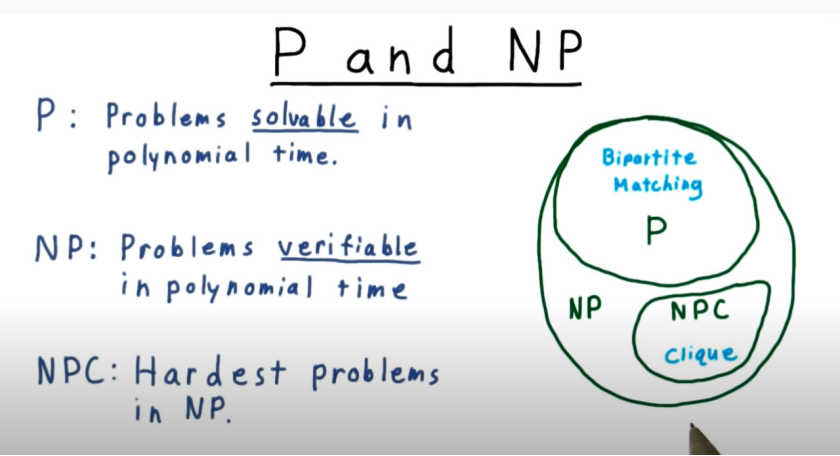
P vs NP

克雷数学研究所官网找到了关于 P和NP问题的简单说明。

简单地翻译过来就是：

假设你正在为400名大学生组织住宿，但是空间有限只有100名学生能留在宿舍里。更复杂的是还给了你一份不相容学生的名单，并要求在你的最终选择中不要出现这份名单中的任何一对。

这是计算机科学家称之为NP问题的一个例子，因为很容易检查一个同事提出的一百个学生的给定选择是否令人满意，然而从头开始找到这100个人的任务似乎太难了以至于完全不切实际。

事实上从400名申请者中选择100名学生的方法总数比已知宇宙中的原子数量还要多！这类问题可以被快速检查，但是通过程序来解决的话则会花费时间太长以至不可接受，比如300年或者更多。

斯蒂芬·库克和列昂尼德·莱文在1971年独立地提出了P(即容易找到)和NP(即容易检查)问题。

P 问题(easy to find)

all problems solvable, deterministically, in polynomial time

多项式时间内可解决的问题(当然在多项式时间是可验证的)

NP 问题(easy to check)

non-deterministic Polynomial time

非确定性多项式时间可解决的问题

大家一定都对算法时间复杂度的大O表示法不陌生吧，简单的来说，时间复杂度并不是表示一个程序解决问题需要花多少时间，而是当问题规模扩大后，程序需要的时间长度增长得有多快。

例如上图所示，增长速度最快的左边两条线是非多项式级的，剩余的是多项式级别的。当我们在解决一个问题时，我们选择的算法通常都需要是多项式级的复杂度，非多项式级的复杂度需要的时间太多，往往会超时，除非是数据规模非常小。

自然地，人们会想到一个问题：会不会所有的问题都可以找到复杂度为多项式级的算法呢？答案是否定的。有的问题甚至找不到正确的算法程序，例如大名鼎鼎的停机问题（The Halting Porblem，可以自行了解下）。

那么P问题与NP问题的关系呢？很显然，所有的P类问题都是NP问题，多项式内被求解的问题一定在多项式时间内被验证。那么所有NP类问题都是P类问题嘛，是否有P=NP这个问题已经困扰了科学家多年时间，不过大部分人还是认为两者不等。虽然无法被证明，但是正是NPC问题的存在，使人们相信P≠NP。NPC问题可以理解为NP问题中最“难”的那一类问题。一个问题A可以约化为问题B，通俗地说就是问题B比问题A难，解决了B就能解决A。举个简单的例子，比如你有了二元一次方程的通解，那你一定能得到解决一元一次方程的通解，因为一元一次方程是二元一次方程二次系数为零的特殊情况。所以说，一个问题约化成另一个问题，所对应的时间复杂度相等或者增加了。

通过不断的约化，能够找到复杂度更高，但应用范围更广的算法来代替复杂度虽低，但只能用于很小一类问题的算法。神奇的事情来了!所有NP问题都可以约化为NPC问题，即如果NPC中任何一个问题能够在多项式时间内找到最优解，则NP中的每个问题都能在多项式时间内找到最优解，即P=NP。遗憾的是，至今为止，对于NPC问题，目前没有多项式的有效算法，只能用指数级甚至阶乘级复杂度的算法。

QAP和NP

理解了P问题，NP问题以及NPC问题以后，大家回想一下之前所说的数独游戏，本质上是一个NP问题，我们找不到一个多项式时间的算法可以算出数独，但是给我数独的解我立刻就可以判断这个数独的解对不对。同样的，schnorr协议中的离散对数难题也是一个NP问题，给任意一个有限域上的整数 r，生成元G，我们就可以在循环群中找到一个对应的点 rG，但是反过来给你rG和G让去找到r是一件很困难的事情，即相对应的，你很难找到schnorr协议里的私钥，但是能很轻松去验证如果有这个私钥到底是不是正确的。

所以来说，需要证明的问题，肯定是NP问题，如果是P问题，不存在问题解的”寻找“，也就不存在证明。zkSNARK问题处理的都是NP问题。

那么问题又来了，我们有如此繁多的NP问题以及最难的NPC问题，我们如何构造一个通用的协议呢？

答案就是我们把任何NP或者NPC问题转化为QAP的形式，而QAP satisfy problem（二次算数程序可满足性问题）是一个NPC问题。简单解释QAP满足性问题即，给一系列的多项式以及一个目标多项式，是否能根据这一系列的多项式，求得它们的一个线性组合，刚好可以整除多项式。即如下描述：

给定一系列多项式，目标
求一个线性组合,使得 ,可记为

这个问题如果给出了一个解，那么验证很简单，直接除t(x)即可验证是否满足，但是想求解就很难。

zkSNARK的思路就是，将原问题的解转化为一个QAP可满足性问题的解，然后公开QAP问题，这样的话拥有解的人用证明公开自己拥有一个解，其他人可以简单验证证明是否成立。

构建R1CS

“V神Vitalik Buterin，以太坊的创始人，是区块链界真正的KOL，是和中本聪同样伟大的存在，在他的博客里描述了如何一步一步构建QAP，接下来加上一些自己粗略的见解，带大家了解整个过程的全貌。

首先，我们要把整个验证过程用代码的形式写出来。比如说在数独游戏中，不允许泄露的信息（即我们自己的答案）称为私有输入（secret input，有时也称witness），而已经填好的数字我们叫公有输入（public input）。我们不妨设私有输入为,

共有输入为，我们接下来要做的就是用代码把约束写出来，也就是每一行每一列和每一个9宫格都是1-9。当然这个例子需要大量的约束条件和代码，我们不妨拿v神博客上简单一些的例子来进行说明。

问题从V神的例子开始，对于方程，显然其解是3，我们（证明者）要向别人（验证者）证明我们知道这个方程的解但是不能向对方透露这个解的知识。

首先，先把方程干的事情通过计算机代码写出来，就像下面这样：

def qeval(x):
y = x**3
return x + y + 5

然后，我们把代码拍平：

拍平后的代码一次只能做下面的一种事情，x=y（x可以是数字或变量）。x=y op z（其中op可以是+，-，*，/等运算）

sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5

在上面的过程中，我们引入了一些中间变量，但是整体跟我们的代码是等价的。

接下来，我们需要把拍平的代码写成一个叫作R1CS（rank-1 constraint system）的东西。

R1CS 是一个由三向量组（a,b,c）组成的序列，R1CS 有个解向量s,s必须满足运算s·a*s·b-s·c=0

表示向量的点积，向量的长度是系统里变量的个数，就像下面这样：

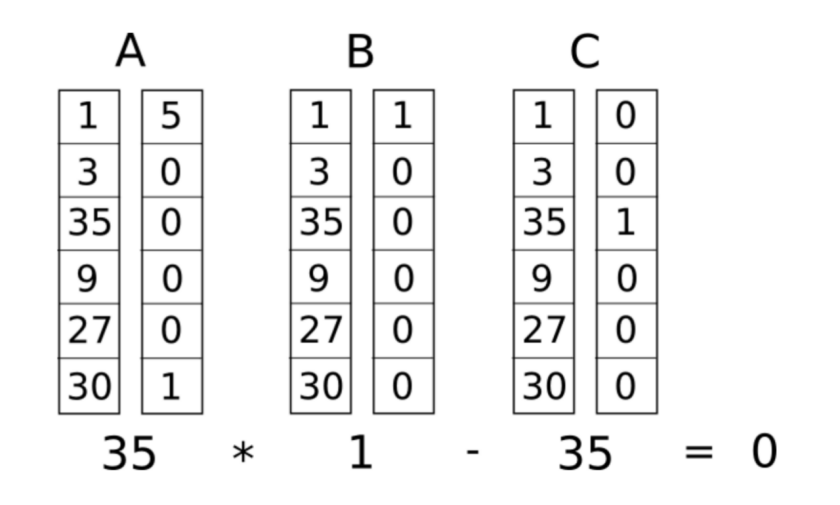
在本例中其解向量的结构即为

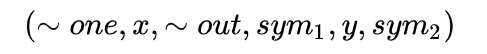
接着我们可以根据程序的第一个等式构造出：

a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]

这实际上就是对程序第一行等式的另一种描述方式。

接下来是第二个等式：

a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]

第三个等式：

a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]

第四个等式：

a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]

于是我们就得到了包含四个约束的R1CS，本质上就是对私密输入，也就是我们的解向量进行了约束。

把向量合在一起，我们就得到了完整的R1CS系统：

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]

B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]

C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]

从R1CS到QAP

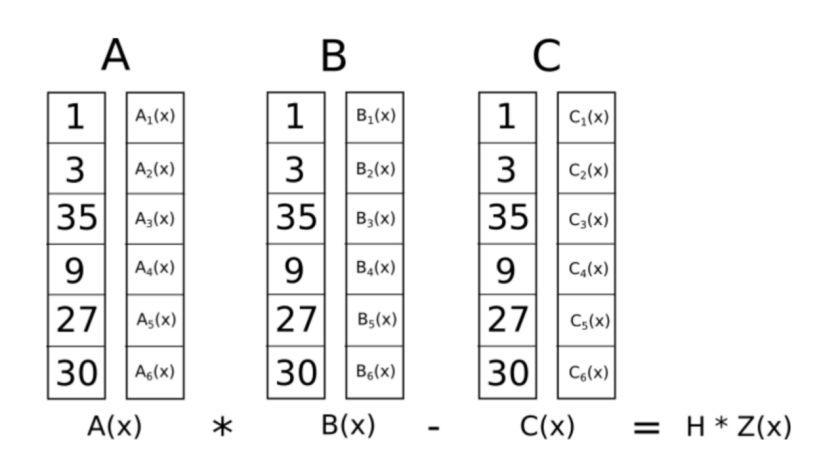
我们可以看到矩阵A，B，C，是一个4乘6的矩阵，我们把矩阵A的第一列拿出来用来构建多项式

选取4个点：

（1，0），（2，0），（3，0），（4，5）

然后求过这4个点的多项式，其中矩阵的值用来当成纵坐标，横坐标我们用1，2，3，4来赋值。

可以得到多项式是

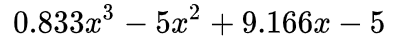
构造多项式的过程可以使用拉格朗日插值法，或者FFT（快速傅里叶变换)，总而言之，我们有四个点，于是可以得到含有四个系数的三次多项式。

然后我们如法炮制，可以得到剩下的多项式

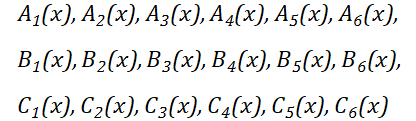
A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]

B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]

C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]

这时候神奇的事情发生了！我们把得到的18个多项式按照下图的方式去排列，把代入多项式得到的值就是我们R1CS矩阵的第一列，得到的值就R1CS矩阵的第二列，得到的值就R1CS矩阵的第三列，根据R1CS的形式

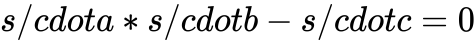
，我们得到这一系列多项式的线性组合在的时候值为0，根据初中学的因式定理，也就是说这一系列多项式的线性组合可以提出因子，同理我们可以提出因子。

所以我们检验四个约束的方式变成检验在

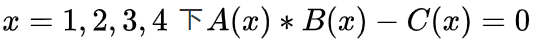
是否成立，也就是检验这个线性组合的多项式有没有因子。

所以我们意识到了我们通过多项式方式所做的操作本质是和R1CS在做同样的事情，这二者是等价的。

这时候我们再看QAP满足问题的描述，是不是发现不知不觉中我们已经把问题转化完毕了，问题的描述如下：

给定一系列多项式，目标
求一个线性组合,使得 ,可记为

其中，对应的就是我们解向量的每一个值，也就是我们的私密输入，对应的是

对应的是我们的，这个问题如果给出了一个解，也就是说我们知道了解向量，

也只有正确的解向量 ,才能使以它为系数的线性组合的多项式整除目标多项式。

至此为止，我们已经完成了构建QAP的全过程。

结语

这篇文章我们简单阐述了计算复杂度中的P问题，NP问题以及NPC问题与QAP的关系，以及我们如何把一个复杂的问题转换到zkSNARK能解决的形式QAP上，我们如何在这个基础上继续构造协议呢？我们后面继续探讨。

文章部分内容参考：

https://vitalik.ca/general/2016/12/10/qap.html

https://blog.ethereum.org/2016/12/05/zksnarks-in-a-nutshell/

RECOMMEND