零知识证明从0到1，ZK简介

ZK简介

最初在1980年提出，由Shafi Goldwasser, Silvio Micali和Charles Rackoff。刚开始叫做交互式证明系统(Interactive proof system)。

Prover和Verifier之间交换信息，让Verifier相信某种statement是真的。

Completeness：诚实的Prover最后会让Verifier相信这个statement。

Soundness：只有statement是真的时候，才能让Verifier相信。

zero knowledge：Prover除了证明这个statement是真的之外，不暴露其他信息。

• Completeness: If the Prover is honest, then she will eventually convince the Verifier.
• Soundness: The Prover can only convince the Verifier if the statement is true.
• Zero-knowledge(ness): The Verifier learns no information beyond the fact that the statement is true.

例子

1. 服务器上面存储了密码的哈希值，用户相当于Prover，服务器是Verifier，用户传输哈希值来证明自己拥有对应的密码，但是服务器不知道哈希值的原像是什么。
2. 三色图问题，可以Prover给图一个解，Verifier随机打开一条边，Prover再打乱这个解。多次交互。可以动手试试

承诺协议

在三色图问题里面，用灰色的点盖住了答案，所以Verifier无法看到答案，但Prover也不可以对答案进行更改了。

在实际中，这样的“灰点”是一个承诺协议：里面加密了一个信息，但同时绑定了这个信息。

承诺方案允许一方 "承诺 "一个给定的信息，同时对其进行保密，然后再 "打开 "所产生的承诺，以揭示里面的内容。承诺协议可以直接由加密的哈希函数构造。可以理解成一个信封✉，我将一个信息放进了信封里面，发送给别人，但之后我可以将信封撕掉，显示出里面的信息。在这个过程中其他人无法看到里面的信息，这是信息的保密性，同时我在证明过程中也无法对信封内的东西进行替换，这是绑定性。

如何证明零知识性质

最终我们得到的是以下定理。如果存在任何Verifier计算机程序，通过与一些Prover交互式地运行该协议，成功地提取某些信息，那么我们可以简单地在该程序上使用倒带技巧，重新提交一个随机的解决方案，一旦不能正确回答其挑战，就通过倒带执行来 "欺骗 "Verifier。与我们上面给出的逻辑相同：如果这样的Verifier在运行真实协议后成功地提取了信息，那么它应该能够从模拟的、基于倒带的协议中提取相同数量的信息。但是，由于没有信息进入模拟协议，所以没有信息可以提取。因此，验证人能够提取的信息必须总是零。

如果对于每一个可能的Verifier，你都能证明存在一种叫做 "Simulator "的算法，并证明这种算法对于verifier来说与现实统计上不可区分，那么一个协议就可以被证明为零知识。

从纯粹的机械角度来看，模拟器就像一种特殊的验证者。然而，与真正的验证者不同的是–它从一些特殊的知识开始，使它能够证明一个语句的真实性–模拟器根本没有得到任何特殊的知识。* 尽管如此，模拟器（或模拟器）必须能够 "欺骗 "每个验证者，使其相信该语句是真实的，同时产生一个在统计上与真正的验证者的输出相同（或不可区分）的记录。

如何证明任意的statement

Goldreich, Micali and Wigderson (GMW)协议允许我们证明一个图的三着色问题。首先三着色问题是一个NP完全问题。所以可以将任意的NP问题规约为三着色问题。

1. 如果存在任何决策问题（即具有是/否答案的问题），其见证（解决方案）可以在多项式时间内得到验证，那么。
2. 我们可以通过以下方式证明上述解决方案的存在：（1）将问题转化为图三色问题的实例，以及（2）运行GMW协议。

证明和证明某个知识

Statements about “facts”. For example, I might wish to prove that “a specific graph has a three coloring” or “some number N is in the set of composite numbers*“.* Each of these is a statement about some intrinsic property of the universe.

Statements about my personal knowledge. Alternatively, I might wish to prove that I know some piece information. Examples of this kind of statement include: “I know a three coloring for this graph”, or “I know the factorization of N”. These go beyond merely proving that a fact is true, and actually rely on what the Prover knows.

第一种和第二种是不一样的：第一种不需要特定的知识也能证明，比如需要证明一个数$n$是合数，并不一定说要知道他的因子是什么；但是第二种证明需要特定的知识，比如$n$的具体的因子有哪些，

由Schnorr身份认证协议来看看ZK的性质，以及如何转为非交互式证明

假设Alice公布了她的公钥$p{k}_A=g^a\mathrm{m}\mathrm{o}\mathrm{d}p$，其中$a\in [1,q]$是私钥，$g$是$q$的生成元，$p,q$是两个素数。

如果Alice要向Bob证明她拥有这个公钥所对应的私钥。那他们运行如下的交互协议。
$$\begin{array}{rlrl}& \mathbf{A}\mathbf{l}\mathbf{i}\mathbf{c}\mathbf{e}& & \mathbf{B}\mathbf{o}\mathbf{b}\\ & \text{Pick random }k\in [1,q]& \stackrel{h=g^k(\mathrm{m}\mathrm{o}\mathrm{d}p)}{\to }& \text{Pick random }c\in [1,q]\\ & & \stackrel{c}{\leftarrow }& \\ & & \stackrel{s=ac+k(\mathrm{m}\mathrm{o}\mathrm{d}q)}{\to }& \text{Check }{g}^s\equiv p{k}_A^c\cdot h\mathrm{m}\mathrm{o}\mathrm{d}p\end{array}$$

completeness

If the Prover is honest, then she will eventually convince the Verifier.

首先，我们应该问自己，该协议是否完备。这通常是最容易验证的属性：如果Alice诚实地执行协议，Bob在协议结束时应该感到满意？在这种情况下，只要做一点替换，完整性就很容易看到。
$$\begin{array}{rlr}{g}^s& \equiv p{k}_A^c\cdot h& \mathrm{m}\mathrm{o}\mathrm{d}p\\ g^{ac+k}& \equiv (g^a{)}^c\cdot g^k& \mathrm{m}\mathrm{o}\mathrm{d}p\\ g^{ac+k}& \equiv g^{ac+k}& \mathrm{m}\mathrm{o}\mathrm{d}p\end{array}$$

Soundness

The Prover can only convince the Verifier if the statement is true.

说到证明知识证明的合理性，我们有一个非常好的形式化方法。就像我们上面讨论的模拟器一样，我们需要证明一种特殊算法的存在。这种算法被称为知识提取器，它所做的正是它所声称的。知识提取器（Extractor）是一种特殊的验证器，它与Prover进行交互，如果Prover成功地完成了证明，提取器应该能够提取Prover的原始秘密。
$$\begin{array}{rlrl}& \mathbf{A}\mathbf{l}\mathbf{i}\mathbf{c}\mathbf{e}& & \mathbf{E}\mathbf{x}\mathbf{t}\mathbf{r}\mathbf{a}\mathbf{c}\mathbf{t}\mathbf{o}\mathbf{r}\\ & \text{Pick random }k\in [1,q]& \stackrel{h=g^k(\mathrm{m}\mathrm{o}\mathrm{d}p)}{\to }& \text{Pick random }{c}_1\in [1,q]\\ & & \stackrel{c_1}{\leftarrow }& \\ & & \stackrel{s_1=a{c}_1+k(\mathrm{m}\mathrm{o}\mathrm{d}q)}{\to }& \\ & & & \text{Extractor rewinds Alice to Step 2}\\ & & \stackrel{c_2}{\leftarrow }& \\ & & \stackrel{s_2=a{c}_2+k(\mathrm{m}\mathrm{o}\mathrm{d}q)}{\to }& \end{array}$$
Extractor可以重置Prover的状态，就比如这里，让Prover给出了两个相同的k。

通过得到了$c_1,c_2,s_1,s_2$，Extractor可以用如下方式恢复Prover的原始秘密。
$$\begin{array}{rl}(s_1-s_2)/(c_1-c_2)\mathrm{m}\mathrm{o}\mathrm{d}q& \\ =((a{c}_1+k)-(a{c}_2+k))/(c_1-c_2)\mathrm{m}\mathrm{o}\mathrm{d}q& \\ =a(c_1-c_2)/(c_1-c_2)\mathrm{m}\mathrm{o}\mathrm{d}q& \\ =a& \end{array}$$

Zero-knowledgeness

The Verifier learns no information beyond the fact that the statement is true.

证明零知识性需要用到模拟器（SImulator），模拟器与Verifier交互，拥有rewind verifier的能力。标准的Schnorr协议是没有这种模拟器的。要证明零知识性，我们要基于一个假设，那就是Verifier是诚实的，也就是他的输入不会随着我们的输入而改变，也就是他会用随机发生器来生成$c$，而不是更具我们发送的值来选。只要有这个假设，就可以构造一个Simulator。

Simulator做如下事情：

1. 首先，输出随便$g^{k_1}$作为第一个消息。然后得到Verifier发送的$c$。
2. 重置Verifier的状态，选一个随机数$z\in [1,q]$。
3. 计算$g^{k_2}=g^z\ast p{k}_A^{-c}$，并输出$g^{k_2}$作为Prover的初始消息。
4. 当Verifier输出$c$作为挑战时，输出$z$。

总结来说，这里Simulator输出的$g^k,c,z$与原始的Prover和Verifier交互是统计上不可区分的。Simulator在不知道$a$的情况下，使得Verifier相信了他的证明，因此Verifier无法从这个证明中提取出$a$的信息。

从交互式证明到非交互式

Fiat和Shamir在1980年发现，只要用一个有效的哈希函数，就可以把一个交互式的证明变为一个非交互式的。

特别地，非交互式证明看起来如下：

1. Prover随机选取$g^k\mathrm{m}\mathrm{o}\mathrm{d}p$。
2. Prover计算一个挑战$c=H(g^k||M)$，其中$H()$是一个哈希函数，$M$是任意消息串。
3. 计算$ac+k\mathrm{m}\mathrm{o}\mathrm{d}q$。

这里一个有意思的点在于，如果$M$是作为一个消息传入的，那么这个方案就可以作为一个Signature方案使用。

三种基础ZK：SNARKS，STARKs，Bulletproofs

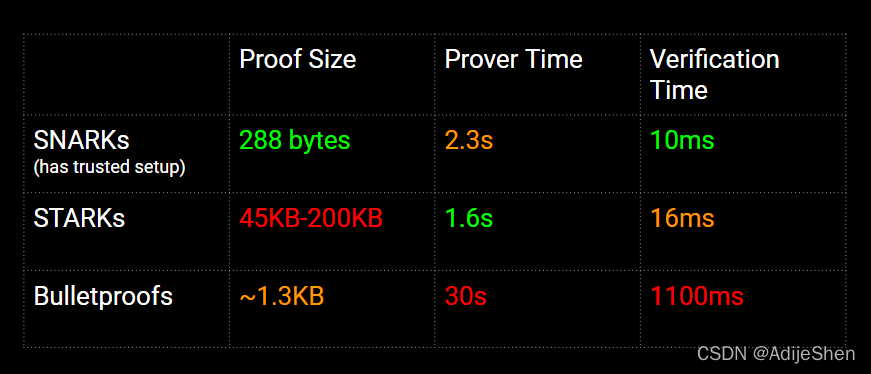
三种协议的开销如上，

从技术上来说：SNARKs¹和STARKs²都是对某种计算的证明，$f(x)=y$，不暴露$x$的情况下证明$y$是由$x$计算出来的。而BulletProof是一种范围证明，用于证明某个数字在$[0,2^n)$中。

在应用中来说：SNARKs是用在Zcash之中的技术，STARKs用在0x上。bulletproof用在门罗币当中，但不是用于保护隐私，门罗币中使用RingCT来保护隐私。

BulletProofs

BulletProofs的思想是一个数字可以表示成二进制形式，如果一个数字的二进制形式有$n$位，那么就可以证明这个数字在$[0,2^n)$中。

在实际使用过程中，令这个数字为$v$，二进制表示为$\mathbf{a}$，则$v=⟨\mathbf{a},2^i⟩$。

要证明的是：

1. $\mathbf{a}$的大小是正确的。
2. 证明我们知道这个值，可以用pedersen承诺加Fiat-Shamir类似的技术来证明。

SNARKs

SNARKs¹有非常多的变种(50+)，SNARKs的基本思路是Computation$\to$Arithmetic Circuit$\to$R1CS³$\to$QAP⁴$\to$SNARKs

由一个算式，比如$x\ast y+4=10$，要不暴露$x,y$的情况下证明这个算式是成立的。

---

先把他转换为算数电路：

---

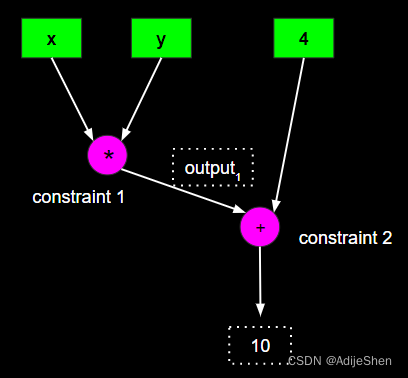
再由算数电路变为R1CS：

R1CS³是一种描述电路的语言。具体来说，一条R1CS由四个向量组成，分别为三个描述向量$\left(L,R,O\right)$，以及一个解向量$v$，要满足
$$⟨L,v⟩\ast ⟨R,v⟩=⟨O,v⟩$$

首先这个算数电路中的Constraint有3个，分别是：

1. ${\text{output}}_1=x\ast y$
2. ${\text{output}}_1+4=10$

将其转换为R1CS，则令$v=[1,x,y,outpu{t}_1]$，对于两个Constraint，分别取:

1. $L=[0,1,0,0],R=[0,0,1,0],O=[0,0,0,1]$

$⟨L,v⟩=x,⟨R,v⟩=y,⟨O,v⟩=outpu{t}_1$

$⟨L,v⟩\ast ⟨R,v⟩=⟨O,v⟩⟺x\ast y=outpu{t}_1$

2. $L=[4,0,0,1],R=[1,0,0,0],O=[10,0,0,0]$

$⟨L,v⟩=outpu{t}_1+4,⟨R,v⟩=1,⟨O,v⟩=10$

$⟨L,v⟩\ast ⟨R,v⟩=⟨O,v⟩⟺(outpu{t}_1+4)\ast 1=10$

---

从算数电路得到QAP⁴:

QAP的构造方式如下，L,R,O都是长度为4的向量，我们构造3*4个多项式$L_i(X),R_i(X),O_i(X),i\in [1,4]$。

拿$L_i(X)$举例，他代表着$L$向量的第$i$个元素，在不同的Constraint下的多项式，也就是说$L_1(1)=0,L_1(2)=4$，通过多项式插值可以得到$L_1(X)=4X-4$

罗列一下所有$L_i(X)$的可得：
$$\begin{gathered} Constraint1:L^{(1)}=[0,1,0,0] \\ Constraint2:L^{(2)}=[4,0,0,1] \\ \begin{array}{rlrlrl}{L}_1(1)& =0,& & L_1(2)=4,& & L_1(X)=4X-4\\ L_2(1)& =1,& & L_2(2)=0,& & L_2(X)=-X+2\\ L_3(1)& =0,& & L_3(2)=0,& & L_3(X)=0\\ L_3(1)& =0,& & L_3(2)=1,& & L_4(X)=X-1\end{array} \end{gathered}$$
可以看出$L_i(n)=L^{(n)}[i]$。

令

$\overrightarrow{L(X)}=(L_1(X),L_2(X),L_3(X),L_4(X))$

$\overrightarrow{R(X)}=(R_1(X),R_2(X),R_3(X),R_4(X))$

$\overrightarrow{O(X)}=(O_1(X),O_2(X),O_3(X),O_4(X))$

很容易验证$\overrightarrow{L(1)}=L^{(1)},\overrightarrow{L(2)}=L^{(2)}$

令

$L(X)=⟨\overrightarrow{L(X)},v⟩$

$R(X)=⟨\overrightarrow{R(X)},v⟩$

$O(X)=⟨\overrightarrow{O(X)},v⟩$

由此可以得到 L ( X ) ∗ R ( X ) − O ( X ) = 0   f o r   X ∈ { 1 , 2 } L(X)*R(X) - O(X)=0~for~X\in\{1,2\} L(X)∗R(X)−O(X)=0 for X∈{ 1,2}

令$P(X)=L(X)\ast R(X)-O(X)$，将$P(X)$拆为两个因子多项式$P(X)=T(X)\ast H(X)$。

其中$T(X)$公开。

这样的$T(X)$其实很容易找，因为$X=1,X=2$是$P(X)=0$的两个根，所以可以令$T(X)=(X-1)(X-2)$，用多项式的除法得到$H(X)$即可。

---

现在要向外部证明的其实是：

$P(X)=L(X)\ast R(X)-O(X)=T(X)\ast H(X)$这样一个式子在所有$X$上成立。

但是公开的多项式只有$T(X)$，也就是说，如果取一个数$X=s$，那么其他人最多能知道$T(s)$的值。那如何在不暴露$L(s),R(s),O(s),H(s)$的情况下证明$L(s)\ast R(s)-O(s)=T(s)\ast H(s)$成了现在要考虑的问题。

那这里就用到了基于椭圆曲线的一种加密：

令$E(s)=sG$，其中$G$是椭圆曲线的一个生成元。

这样的加密如下性质：

1. 单项性：给定$x$，很容易计算$y=E(x)$，但给定$y$，很难找到一个$x$满足$y=E(x)$。
2. 线性：$E(\alpha x+\beta y)=\alpha E(x)+\beta E(y)$
3. 单射：$x\ne y⟶E(x)\ne E(y)$

所以Prover可以直接计算出$P(E(s))=E(P(s))$的值。

SNARKs的协议如下：
1. Setup: 将$E(s)$公开，$T(s)$公开，$s$本身丢弃 2. Prover自己有$L,R,O,H$四个多项式 3. Prover发送$E(L(s)),E(R(s)),E(O(s)),E(H(s))$ 4. 任何人都可以验证： $E(L(s))\ast E(R(s))-E(O(s))=E(H(s))\ast E(T(s))$

小结：

这里省略了很多的细节，只讲了大概的框框，包括SNARKs是否满足ZK的三个性质是没证明的，所以看到这里应该还没被说服，为啥只要给出了这个证明就得相信这个计算是正确的？其实就是Completeness和Soundness没有证明嘛。
省略的细节包括椭圆曲线，$s$其实还要做盲化，要不然不是Zero-knowledge，以及一些配对相关的东西。

区块链扩容

区块链扩容包括了两层

1. 对区块链本身进行扩容，让他能存更多的交易。这类扩容的例子有Ethereum,Eth2x,DFinity, Polkadot,Cosmos，用到的技术有Sharding, Pruning, State rent, WASM, PoS, Casper, Light clients, ZKPs.
2. 在分布式应用中尽量少的依赖区块链。比如Dapps，代表性的有Plasma Cash, Ignis，Rollup。

ZKP如何做扩容？

ZKP是解决了这样一个问题：$F(X,Y)=Z$，其中$F$是任意函数，$X$是公开的输入，$Y$是私有的输入，$Z$是公开的输出。

这里$Y$除了可以当做一个隐私信息，还可以作为一个批量的信息源，比如$X$和$Z$都是几十byte，而$Y$是几MB的消息。比如在区块链中，$F$可以是验证交易以及更新账本，$X$是先前值的Merkle root，$Z$是当前值的Merkle root，$Y$是一整个Merkle tree。

目前ZKP的技术可以一次操作处理500个交易。Prover的时间是25分钟，目标是降到10分钟（2019年的演讲）。

---

1. Succinct Non-interactive ARguments of Knowledge ↩︎ ↩︎

2. Succinct (Scalable) Transparent ARguments of Knowledge ↩︎

3. Rank-1 Constraint Satisfaction ↩︎ ↩︎

4. Quadratic arithmetic program ↩︎ ↩︎