考研之数据结构023_图的经典应用（最小生成树、prinm/Kruskal、最短路径-BFS-Dijkstra-floyd）

一、最小生成树的概念（Prim、Kruskal）

1、概念

• 连通图的生成树是：包含图中全部顶点的一个极小连通子图
• 若图中顶点数为n，则它的生成树含有n-1条边。
• 对生成树而言，若砍去它的一条边，则会变成非连通图，若加上一条边则会形成一个回路。
• 用偏理解的话来解释：什么是生成树：
• 对于一个连通的无向图，若能找到子图，子图包含它所有的顶点，并且所有的顶点还能连通。边的数量：n-1条。就是生成树。
• 一个连通图，可能有多个生成树。

2、最小生成树（最小代价树）

• 一个带权的连通树无向图，有多个生成树。找到各权值之和最小的那棵树。就是最小生成树。
  

二、Prim算法（每次将代价最小的新顶点纳入生成树）

• 从某一个顶点开始构建生成树；
  每次将代价最小的新顶点纳入生成树，直到所有顶点都纳入为止。

• 没有纳入生成树的新结点，代价最小的结点，将至纳入生成树中。

• 时间复杂度：之和顶点有关系

三、Kruskal算法（每次选择代价最小的一条边使两个顶点连通）

• 每次在整个图中去选择一条边权值最小的，将两个点连通，结点已经在生成树的不进行连接。直至所有的结点全部连通。

• Kruskal算法是：每次选择代价最小的一条边使两个顶点连通

• prinm算法是：每次将代价最小的新顶点纳入生成树

• 时间复杂度：之和边有关系

四、最短路径

1.都不能解决“带负权回路的图”
2.dijkstra算法，也可以求所有顶点之间的路径，重复|v|次就可以，分别以n个顶点作为元顶点，来求此顶点到达其他路径。本身重复n次，再乘以时间复杂度v的平方，总的时间复杂度和floyd算法一样都是v³。
3.广度BFS算法：时间复杂度开销是：访问各个顶点和各条边。
3.1如果是用邻接矩阵来存储的话，查找所有的边需要o(N)²。
3.2如果用邻接表存储的话，查找各条边需要o(v+e)。
4.所以BFS算法，时间复杂度有两种。

五、单源最短路径（BFS广度优先算法-无权图—考研常考1）

• 只有单独一个源头，从这个源头出发，到达任意一个原点可以走的最短路径。
• 用广度优先算法：
• 第一个d[]数组：是用来表示：各个顶点到原始顶点的最短路径的长度（默认都是1）
• 第二个path[]数组：来表示：每一个顶点在这个最短路径上的，直接前驱。

• 代码的分析：

2号节点开始到达其他节点的路径，u=2

• for循环，将每一个结点都进行初始化

d[]数组是：各个顶点到原始顶点的路径。初始化，赋值为无穷。
path[]数组是：每个顶点的直接前驱。初始化，赋值为-1
2号是起始顶点，将值赋值d[u] 赋值为0
visited[] 数组是：是否被访问过。此时为true
EnQueue（Q,u）并将入栈
…进行while循环
，如果队列非空的话，则进入while循环
弹出队列，
…并进入for循环：
for（第一个顶点：顶点大于0；下一个顶点）
依次判断顶点的邻点，是否被访问过
如果被访问过，则进入for循环下一个邻接点
没有被访问过则：
d[]数组：…
也就是顶点的位置初始化是0，+1.赋值给此时正在访问的结点（顶点的邻接点）
也就是在说：从顶点的位置到此时访问结点的距离是多少。
path[]数组：…
记录直接前驱。也就是说记录此时访问的结点，是由于哪个顶点过来的。
访问过了以后，记录 visited[]数组为true，表名已经被访问过了。
将此时访问的顶点入队。
…
直到队列为空，停止while循环。表明所有节点都已经访问过了。

---

看下面的两个数组表，来反应数据：
2到8的最短路径长度为=d[8]=3
通过Path[]数组可知：2到8的最短路径为：8->7->6->2
path[8]=7
7->6
6->2.

---

六、单源最短路径–Dijkstra算法-带权图、无权图—考研常考2。分值10分）

带权路径长度：当图是带权图时，一条路径上所有边的权值之和，称为该路径的带权路径长度。

• 例子：例如从v0到其他顶点的各个路径。那么需要初始化三个数组：
  1、final[0]：【标记各顶点是否已找到最短路径】目前为止有无找到v0到达该路径的最短路径。初始化的时候，将起始地点设为true。
  2、dist[]：【最短路径的长度】。目前为止，找到v0到达该路径的最短长度。
  3、path[]:【路径上的前驱】。记录每一个顶点，最短路径上的直接前途。

-举例子进行演示：
1.循环遍历所有的结点数组信息，从中找到目前还没有确定最短路径的顶点，并且dist最小的顶点（也就是说最短路径长度）。确定好最短路径是：v4，并将final设为true
2.检测和v4相连的顶点（v123）。此情况是检查v4到v1：直接从v0到v1需要长度为10。v1如果从v4过来的话，只需要3。而v0到v4需要5.加起来是8。会更好。所以会更改：dist[1]=8（最短路径），并将path[1]=4（上一路径是4号）。
2.1：继续检查v4到v2，之前到达v2需要的是无穷，现在通过v4过去，需要14。所以将数组dist改为14。path[2]=4 。 同理v4到v3。
3.第二轮处理和第一轮处理同样的：
3.1：遍历各节点是否已经找到最短路径，并且dist值最小的是那个顶点
3.2：将该顶点的final设为true。
3.3：检查可以从v3过去的顶点（只检查final为false顶点，为true的顶点不用处理）。
3.4：拿该顶点的dist值，与过该顶点的路线长度，进行对比。如果过该顶点比之前顶点的dist值大，那么就将dist值改为小的值。将path值改为出发的顶点值。
一直重复…以上2/3步骤，直到final数组值没有false为止。

七、各顶点间的最短路径-Floyd（带权图、无权图）

一、总体介绍

1.floyd可以解决负权值带权图，但是不能解决“负权回路”的图

解释下图：
我们要求的是：i到j的最短路径：
1.初始化：不允许中转的路径。
2.经过v0中转，是否有优化，若有则代替. ———————— 第1次求解
3.经过v0,v1中转，是否有优化，若有则代替。——————— 第2次求解
4.经过v0,v1,v2…vn-1中转，是否有优化，若有则代替。—— 第n次求解

所以我们要经过n次求解（n个顶点，设某一个顶点，其他任意两个顶点，若经过此顶点， 是否有优化路径。）

---

二、例子进行疏导解释：

• 用例子进行一遍疏导：

1、A和path数组初始化：

一、Floyd各顶点间的最短路径。将进行设置两个二维数组矩阵：
1.A[][]数组：图中的邻接矩阵，用来表示，当前各顶点间的最短路径长度。 初始化是，并没有中转的路径长度。
----1.1：如何看二维数组：
--------例如从i到j的路径长度是多少：i是看行，j是看列。 i行到J列是多少。
------------举例子：V0到V1是6，V1到V0是10。 I是看行，J是看列

2.path[][]数组：目前，我们能找到最短路径的，两个顶点之间的中转点。 初始化：没有中转点，所以将所有的值设为-1.

3.总图的概括：

2、若经过V0中转，是否有优化路线

二、遍历A矩阵，如果各个顶点之间，在v0中转，最短路径是否有优化。求A0和path0数组。

1.遍历矩阵A，对于矩阵A每一个元素，进行检查。 初始化并没有中转点，如果加入了中转点V0是否有优化，例如V2到V1的初始化路径长度是无穷，经过了V0以后，是否有优化，经过V0后路径长度是：11。 【V2-V1 > V2-V0+ V0-V1 】
—那么更改两个数组的信息：
------1.1：在A数组中：更改A[2][1]的值为11. 也就是说目前v2到v1的最短路径是11。
------1.2：在path数组中：更改v2到v1的值为0，path[2][1]=0。 说明目前从V2到V1的最短路径是从v0中转过来的。

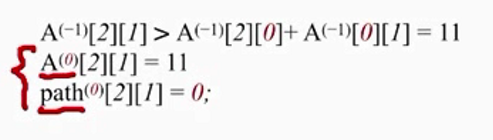
代码：

A0和path0数组：

3、若经过V1中转，是否有优化路线

三、.经过V1中转，是否有优化路径，也就是求A1和Path1.
3.1：遍历A数组， 从中找出，从i到J的路径，从V1顶点进行中转，是否优于，之前从i到J的路径。

3.2：得知若某两个顶点经过V1中转，是有优化的。
：V0到V2=13 是大于 V0中转V1再到V2是10。

3.3：将更改A、path数组。
将A[0][2]中是13，现在更改为10。说明目前从V0到V2的最短路径是10
将path[0][2]中是-1，现在该为1， 说明目前从V0到V2的最短路径是从v0中转过来的。

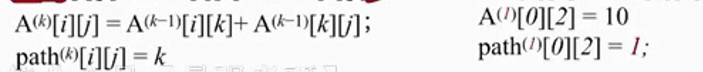
4、若经过V2中转，是否有优化路线

四、.经过V2中转，是否有优化路径，也就是求A2和Path2.

5、经过了n轮递推（n是结点的个数）

五、从A0到A2，经过了n轮递推。
通过两个矩阵A和path数组，从而可以得到任意两点最短路径和长度。

6、核心代码：