基本概念
P1:递归_recursive processing
1.估计值
典型的就是拿尺子量同一个物体,记为 z 1 , z 2 . . . z_1,z_2... z1,z2...,那么估计值可以表示为
x ^ k = 1 k ( z 1 + z 2 . . . z k ) = 1 k ( z 1 + z 2 . . . z k − 1 ) + 1 k z k = k − 1 k 1 k − 1 + 1 k z k = k − 1 k x ^ k − 1 + 1 k z k = x ^ k − 1 + 1 k ( z k − x ^ k − 1 ) \hat{x}_k = \frac1k(z_1+z_2...z_k)\\ = \frac1k(z_1+z_2...z_{k-1})+ \frac1kz_k\\ =\frac{k-1}k\frac1{k-1}+ \frac1kz_k\\ =\frac{k-1}k\hat{x}_{k-1}+ \frac1kz_k\\ =\hat{x}_{k-1}+ \frac1k(z_k-\hat{x}_{k-1}) x^k=k1(z1+z2...zk)=k1(z1+z2...zk−1)+k1zk=kk−1k−11+k1zk=kk−1x^k−1+k1zk=x^k−1+k1(zk−x^k−1)
随意随着k的增加,测量值变得不再重要,可以很相信估计的结果。
所以我们可以得出:当前的估计值=上一次的估计值+系数X(当前测量值-上一次估计值):系数记为 K k K_k Kk,kalman gain 卡尔曼增益系数
估计误差:估计值和真实值的差距(残差), e E S T e_{EST} eEST
测量误差:测量值和真实值的差距, e M E A e_{MEA} eMEA
可以得到 K k = e E S T k − 1 e E S T k − 1 + e M E A k K_k=\frac{e_{EST_{k-1}}}{e_{EST_{k-1}}+e_{MEA_{k}}} Kk=eESTk−1+eMEAkeESTk−1
当k-1时的估计误差远大于k时的测量物测,那么第k次的估计值就很接近测量值。
即: e E S T k − 1 > > e M E A k , x ^ k = x ^ k − 1 + z k − x ^ k − 1 = z k e_{EST_{k-1}}>>e_{MEA_{k}}, \hat{x}_k=\hat{x}_{k-1}+z_k-\hat{x}_{k-1}=z_k eESTk−1>>eMEAk,x^k=x^k−1+zk−x^k−1=zk就是估计的误差大,就更信任测量值。同理,如果测量误差大,那么估计值应该更相信估计值。
估计误差的更新: e E S T k = ( 1 − k k ) e_{EST_{k}}=(1-k_k) eESTk=(1−kk)e_{EST_{k-1}}$

如上图是一个小例子:初值我们可以预先设定(测量误差为3,设备给定不可变,其他参数随意给值会自己迭代),然后通过公式迭代计算。
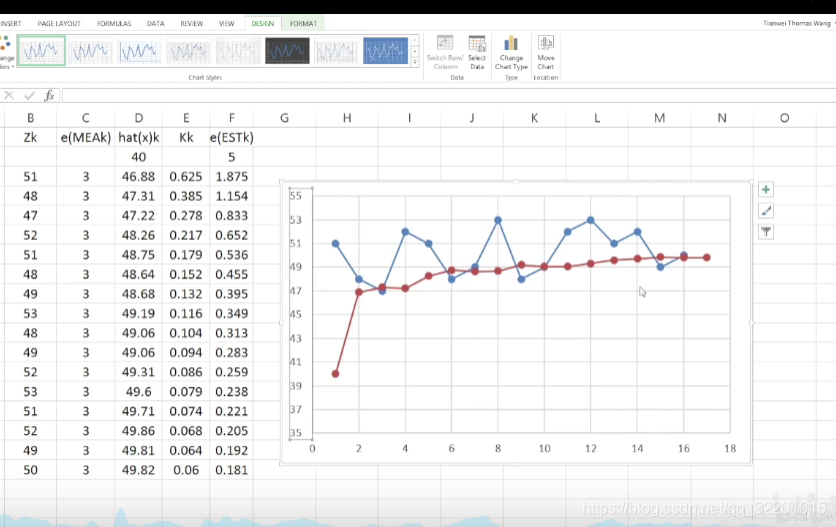
可以利用excel迭代运算,红线处理过对的结果更加平滑
P2 2_数学基础_数据融合_协方差矩阵_状态空间方程_观测器问题
- Data Fusion数据融合

假设有2个称,去称一个东西,得到了2个结果,而且他们也都有误差:
z 1 = 30 , σ = 2 ; z 1 = 32 , σ = 4 z_1=30,\sigma =2;z_1=32,\sigma =4 z1=30,σ=2;z1=32,σ=4可以画出他们的分布曲线。
现在我们可以估计一个真实值,那么应该在二者之间。
我们可以引入K,来估计他的值。
这时我们求k来使得他的标准差最小,也是方差最小,

通过分析求导得到,他的最优解应为30.4g,方差为3.2
2.covariance matrix 协方差矩阵

可以从例子入手,这里有英超的3个球员的身高体重年龄,然后求平均数,然后求方差。然后计算协方差,可以看出他们是正相关还是负相关。
在运用时,可以先求一个过度矩阵,对于以后编程会比较有用:
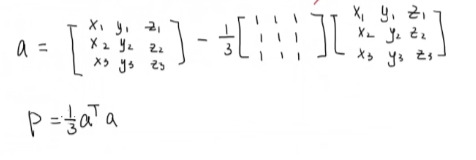
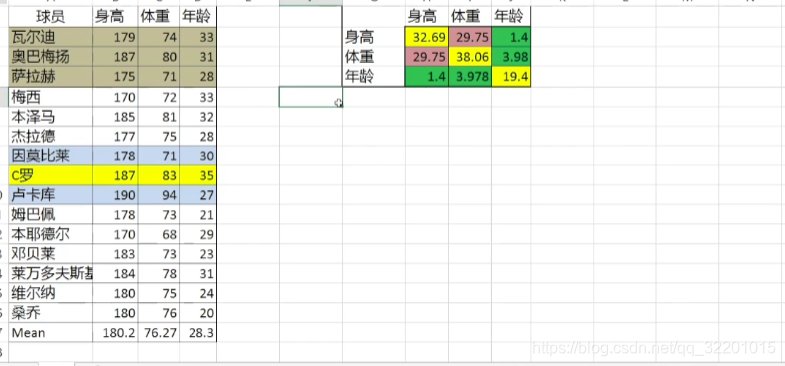
然后介绍协方差说明了什么:这里给出15个球员,然后算出他的协方差矩阵,通过方差可以看出成为一个射手,身高,体重,年龄的跨度都比较大,所以对身高,体重,年龄都没有特别的要求。然后看到协方差,身高体重是正相关的,随着身高增加,体重也随之增加,相关性很高,然后是年龄与体重身高的关系,这个系数就很小,说明运动员随着年龄变换,但是身材保持的还是很好的。
3.状态空间表达: state space representation
还是从例子下手:首先列一个弹簧的受力方程,然后我们可以假定状态量 x 1 , x 2 x_1,x_2 x1,x2,这样我们可以用2个一阶微分方程来表示他的状态。这里我们带入他们所代表的测量了,然后写成矩阵的形式

这时连续的形式,如果离散的话我们可以写为(不是照抄,改的时候也要考虑采样时间),最后再加上噪声,模型不准确,测量也不准确,如何得到精确的结果呢,这就是kalman滤波所做的事。

P3_卡尔曼增益超详细数学推导
状态空间方程:
X k = A X k − 1 + B u k − 1 + w k − 1 z k = H X k + v k X_k= AX_{k-1}+Bu_{k-1}+w_{k-1}\\ z_k = HX_k+v_k Xk=AXk−1+Buk−1+wk−1zk=HXk+vk
X_k:状态变量
A:状态矩阵
u_k:控制
B:控制矩阵
w_{k-1}:过程噪声
z_k:测量结果
v_k:测量噪声
所限假设自然界的噪声都符合正太分布,则噪声可以表示为 P ( ω ) ( 0 , Q ) P(\omega)~(0,Q) P(ω) (0,Q), Q Q Q为协方差矩阵,0为期望。
因为噪声我们不知道,所以我们可以先求出先验估计结果,然后测出来的结果,我们可以H逆来算出新的结果
X ^ k − = A X k − 1 + B u k − 1 X ^ k M E A = H − Z k \hat{X}_k^-=AX_{k-1}+Bu_{k-1}\\ \hat{X}_{kMEA}=H^-Z_k X^k−=AXk−1+Buk−1X^kMEA=H−Zk
这两个结果都是不太准确的,没有考虑噪声,估计值为
X ^ k = X ^ k − + G ( H − Z k − X ^ k − ) , G ∈ [ 0 , 1 ] \hat{X}_k=\hat{X}_k^-+G(H^-Z_k-\hat{X}_k^-),G\in[0,1] X^k=X^k−+G(H−Zk−X^k−),G∈[0,1]
当G=0时,估计值为先验估计。G=1时,估计值为测量值。
教科书上的公式其实是:
X ^ k = X ^ k − + K k ( Z k − H X ^ k − ) , K k ∈ [ 0 , H − ] \hat{X}_k=\hat{X}_k^-+K_k(Z_k-H\hat{X}_k^-),K_k\in[0,H^-] X^k=X^k−+Kk(Zk−HX^k−),Kk∈[0,H−]
这时我们的目标是去寻找一个 K k K_k Kk使得 X ^ k − > X k \hat{X}_k->X_k X^k−>Xk,那么我们可以想到 K k K_k Kk的取值肯定与噪声有关,如果测量噪声很大,那么肯定相信估计值多一点。
设误差为 e k = X k − X ^ k e_k=X_k-\hat{X}_k ek=Xk−X^k,他的分布可以表示为方差为P的正太分布,P为他的协方差矩阵。
此时目标变为寻找一个 K k K_k Kk,使得协方差矩阵P的迹最小,后面求期望,过程有点长,需要看懂建议看原版视频:

后面迹对 K k K_k Kk求导:


最终算得kalman最重要的增益方程
P4_误差协方差矩阵数学推导_卡尔曼滤波器的五个公式
在之前我们算出来了:

我们可以看到先验估计是已知的,后验的话我们未知 K k K_k Kk,所以我们要求处理,要求 K k K_k Kk的话,那么我们要求出 P k − P_k^- Pk−
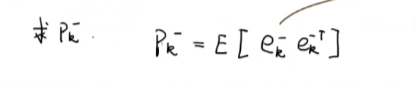



此时我们可以进行预测和校正了

P5_直观理解与二维实例
EXCEL程序下载链接
提取码:txn3,文件密码为下面这道题的答案:

EXAMPLE:

根据状态我们可以列出状态矩阵,然后找到最优的估计,这就是kalman滤波器的用处。五个式子:

然后可以通过excel来进行调试
P6_扩展卡尔曼滤波器_Extended Kalman Filter
首先revisit 线性系统
X k = A X k − 1 + B u k − 1 + ω k − 1 , P ( ω ) ∼ N ( 0 , Q ) Z k = H k − 1 + v k , P ( v ) ∼ N ( 0 , R ) X_k=AX_{k-1}+Bu_{k-1}+\omega_{k-1} ,P(\omega)\thicksim N(0,Q)\\ Z_k=H_{k-1}+v_k ,P(v)\thicksim N(0,R) Xk=AXk−1+Buk−1+ωk−1,P(ω)∼N(0,Q)Zk=Hk−1+vk,P(v)∼N(0,R)
然后是预测和校正

接下来考虑非线性系统,这里仍然考虑误差为正太分布,但是正态分布的随机变量经过非线性系统之后将不再是正态分布的,如果要继续使用卡尔曼滤波,那么要把它转换成线性的,这时我们通过泰勒展开(相关数学知识可以上网查找)转换。即
f ( x ) = f ( x 0 ) + ∂ f ∂ x ( x − x 0 ) f(x)=f(x_0)+\frac{\partial f}{\partial x}(x-x_0) f(x)=f(x0)+∂x∂f(x−x0)
对于我们线性化而言,我们必须要找到一个点,然后在他周围线性化,最好是选真实值,但是真实值是有误差的,所以退而求其次,利用上一次的后验估计来求。

A与后验估计有关,所以每一步都要重新算A矩阵,然后进行线性化

然后修改预测和校正方程
