CINTA作业9

第一题

证明：

封闭性：

任取 p, q ∈ QR_p, 设 p ≡ x² (mod n) , q ≡ y² (mod n) , 则有 p*q ≡ (x*y)² (mod n), 即 p*q ∈ QR_p, 封闭性得证

结合性：

乘法结合性显然。

单位元：

必然存在 m = 1, x = 1, 使得 m ≡ x^2 (mod n) , 即必然有 1 ∈ QR_p, 而对于任意 x , 都有 1 * x = x, 即 QR_p 必然存在单位元 1 。

逆元：

$$对任意m\equiv x^2(modn),有m\ast (x^{-1}{)}^2\equiv 1,即m存在逆元(x^{-1}{)}^2$$

第二题

用群论的方法证明：

对 {Z_p}^* 中的所有整数做平方，映射到模 p 的 QR。命题11.1告诉我们，恰好有两个

不同余的整数映射到一个 QR。现在我们有 p − 1 个平方要考虑，则恰好有 (p − 1)*/*2 个

模 p 的 QR。剩下的 (p − 1)*/*2 整数就是模 p 的 QNR。

第三题

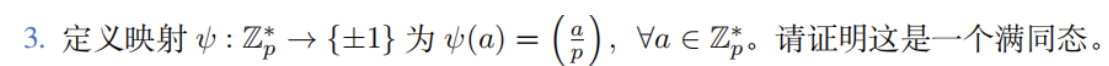
a ∈ {Z_p}^*, 即不存在 p | a, 由勒让德符号的定义可得这是一个满射, QR -> 1, QNR -> -1.

ψ(ab) = (ab/p) = (a/p)(b/p) = ψ(a)ψ(b), 即是一个同态

第四题

$$

反证法：&令g为Z_p^*的生成元,且g为QR,则有g≡a²(modp)
则g的阶为p-1,g^{p-1}≡a{2(p-1)}≡1(modp)
则g^(p-1)/2≡a^p-1≡1(modp)
则g的阶为(p-1)/2,与前面矛盾

$$

第五题

证明：

1

由定义可得

2

由命题11.3:QR*QR=QR;QR*QNR=QNR;QNR*QNR=QR可得

3

令a²=t, 由定义可得 原式=(t/p)=1

第六题

证明：
$$

p≡-1(mod4)意味着存在k∈Z使得p=4k-1。根据欧拉准则，
(-1/p)≡(-1)^(p-1)/2≡(-1)^(4k-1-1)/2≡-1(mod4)

$$