半球上的Hammersley
源作者:Holger Dammertz
一组关于如何在2D中使用Hammersley点集以在着色器程序中快速实用地生成半球方向的笔记。如果你发现任何错误或有意见,不要犹豫,请联系我或在我的博客上留言。
1. 概述
在编写与光照有关的着色器时,人们经常需要一些以表面法线为方向的半球方向。通常的做法是预先计算这些方向,并将它们存储在一个静态/统一的数组中,或者创建一个包含这些方向的可查询的纹理。在这一页,我研究了如何在着色器中直接使用2d中的Hammersley点集来快速计算合理的分布方向。当然,这个点集并不局限于取样方向,它还可以用于阴影图过滤、屏幕空间环境遮蔽(SSAO)或其他任何需要2D取样模式的应用。
二维的Hammersley点集是最简单的低差异序列之一,在计算机图形中的伪蒙特卡洛(Quasi Monte Carlo)集成方面有许多可能的应用。对各种不同的伪蒙特卡罗序列的总体概述可以在Niederreiter [niederreiter92]的书中找到。例如在 [wong97]中可以找到明确使用Hammerysley点集进行球体采样的方法。
下面我首先简要介绍一下如何从数学上构造Hammersley点集,然后展示这些点在2d中的样子,以及它们在映射到半球时的样子。之后,我向你展示了一个可以直接插入GLSL着色器中的实现(或者很容易翻译成任何其他语言)。
2. Hammersley点集
我们考虑一个点集 P N = { x 1 , . . . , x N } P_N=\left\{ x_1,...,x_N \right\} PN={
x1,...,xN} 与点的数量 N ≥ 1 N≥1 N≥1在二维单位面积上 [ 0 , 1 ) [0,1) [0,1)(原本中关于此处均使用左闭右开)。Hammersley点集 H N H_N HN,在2D中,现在被定义为
H N = { x i = ( i / N Φ 2 ( i ) ) , f o r i = 0 , . . . , N − 1 } ( 1 ) H_N=\left\{ x_i=\left( \begin{array}{c} i/N\\ \varPhi _2\left( i \right)\\ \end{array} \right) ,for\,\,i=0,...,N-1 \right\} \,\, \left( 1 \right) HN={
xi=(i/NΦ2(i)),fori=0,...,N−1}(1)
其中 Φ 2 ( i ) \varPhi _2(i) Φ2(i)是Van der Corput序列
Van der Corput序列的想法是在小数点处镜像 i i i的二进制表示,以得到区间[0,1]中的一个数字。
Van der Corput序列 Φ 2 \varPhi _2 Φ2的数学定义如下:
Φ 2 ( i ) = a 0 2 + a 1 2 2 + . . . + a r 2 r + 1 ( 2 ) \varPhi _2\left( i \right) =\frac{a_0}{2}+\frac{a_1}{2^2}+...+\frac{a_r}{2^{r+1}}\,\, \left( 2 \right) Φ2(i)=2a0+22a1+...+2r+1ar(2)
其中 a 0 a 1 . . . a r a_0a_1...a_r a0a1...ar是 i i i用二进制表示的各个数字(i.e. i = a 0 + a 1 2 + a 2 2 2 + a 3 2 3 + . . . a r 2 r i=a_0+a_12+a_{2}2^{2}+a_{3}2^{3}+...a_{r}2^r i=a0+a12+a222+a323+...ar2r).
2.1 Radical Inverse Examples
这一点最好通过一个例子来理解。在下面的表格中,我给出了 i i i的十进制和二进制表示,以及相关的Van der Corput基数逆(radical inverse)(如公式2中的定义),在小数点处二进制表示。为了便于理解,我还在 i i i的二进制表示中加入了小数点,尽管在考虑二进制整数时通常会省略这一部分。
| i i i decimal | i i i binary | Φ 2 ( i ) Φ_2(i) Φ2(i) binary | Φ 2 ( i ) Φ_2(i) Φ2(i) decimal |
|---|---|---|---|
| 0 | 0000.0 | 0.0000 | 0.0 |
| 1 | 0001.0 | 0.1000 | 0.5 |
| 2 | 0010.0 | 0.0100 | 0.25 |
| 3 | 0011.0 | 0.1100 | 0.75 |
| 4 | 0100.0 | 0.0010 | 0.125 |
| 5 | 0101.0 | 0.1010 | 0.625 |
| … | |||
| 11 | 1011.0 | 0.1101 | 0.8125 |
| … | |||
该表显示了 Van der Corput序列中的前几个数字。它只是 i在小数点处镜像的二进制表示。
这种简单的镜像二进制表示法使得Hammersley点集称为在着色器中快速和容易实现的点集的理想人选。在我讨论代码之前,我想向你展示点集在2D中的实际情况。
2.2 Hammersley点集图像
在这个交互式图像中,你可以改变点的数量 N N N,并得到由公式1定义的、在单位方格 [ 0 , 1 ) 2 [0,1)^2 [0,1)2中可视化的结果点集。你可以看到,点 ( 0 0 ) \left( \begin{array}{c} 0\\ 0\\ \end{array} \right) (00)总是这个序列的一部分。你还可以看到,对于任何数量的N个点来说,这些点的分布都很好

3. 生成半球上的点
为了从 H N H_N HN创建半球上的方向,可以使用从 [ 0 , 1 ) [0,1) [0,1)到半球的任何映射,但必须注意所选择的映射要满足应用的要求。在光传输背景下进行积分时,通常需要球面上的均匀或余弦加权分布。
让 x i = ( u v ) ∈ H N x_i= \left( \begin{array}{c} u\\ v\\ \end{array} \right) ∈H_N xi=(uv)∈HN是我们选择的Hammersley点集的一个点。让两个坐标 u u u和 v v v,我们现在可以计算处以下的映射。把球坐标系转成直接坐标系即可。
3.1 统一映射
θ = c o s − 1 ( 1 − u ) ϕ = 2 π v θ=cos^{-1}(1-u)\\ ϕ=2πv θ=cos−1(1−u)ϕ=2πv
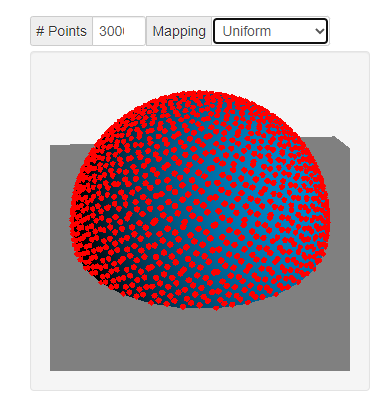
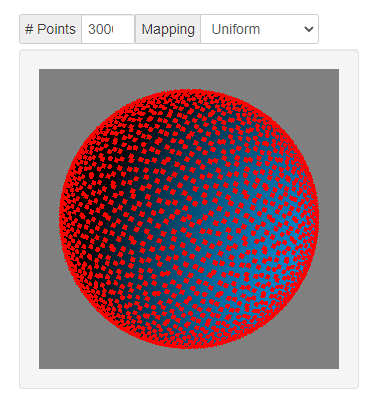
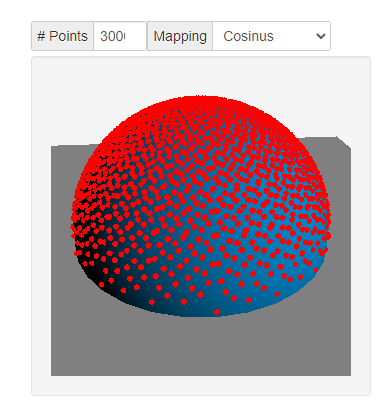
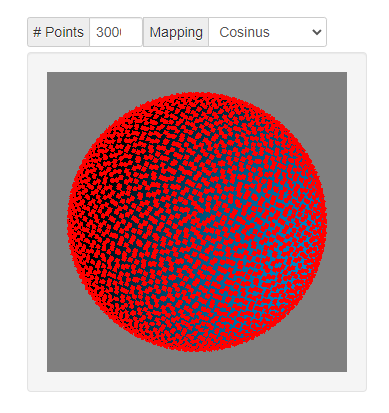
3.2 余弦映射
θ = c o s − 1 ( ( 1 − u ) ) ϕ = 2 π v θ=cos^{-1}(\sqrt{(1-u)})\\ ϕ=2πv θ=cos−1((1−u))ϕ=2πv
4. 源代码
为了实现Hammersley点集,我们只需要一个有效的方法来实现Van der Corput基数逆(radical inverse) Φ 2 ( i ) Φ_2(i) Φ2(i)。由于它是以2为基数的,我们可以使用一些基本的位操作来实现。Hacker's Delight [warren01]这本书为我们提供了一个简单的方法来反转一个给定的32位整数的位。使用这个方法,下面的代码就可以在GLSL中实现 Φ 2 ( i ) Φ_2(i) Φ2(i)
float radicalInverse_VdC(uint bits) {
bits = (bits << 16u) | (bits >> 16u);
bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);
bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);
bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);
bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);
return float(bits) * 2.3283064365386963e-10; // / 0x100000000
}
然后通过以下方式计算出第 i i i个点 x i x_i xi
vec2 hammersley2d(uint i, uint N) {
return vec2(float(i) / float(N), radicalInverse_VdC(i));
}
一个小的优化是将上面的代码中除以N的部分改为乘以它的逆数,因为无论如何N都需要被固定。
为了完整起见,这里还有从Hammersley点集 x i = ( u v ) {x_i= \left( \begin{array}{c} u\\ v\\ \end{array} \right) } xi=(uv)创建均匀或余弦分布方向(z-up)的代码。请注意,代码中的 1 − u 1-u 1−u是必要的,以便将序列中的第一个点映射到向上的方向而不是切平面。
const float PI = 3.14159265358979;
vec3 hemisphereSample_uniform(float u, float v) {
float phi = v * 2.0 * PI;
float cosTheta = 1.0 - u;
float sinTheta = sqrt(1.0 - cosTheta * cosTheta);
return vec3(cos(phi) * sinTheta, sin(phi) * sinTheta, cosTheta);
}
vec3 hemisphereSample_cos(float u, float v) {
float phi = v * 2.0 * PI;
float cosTheta = sqrt(1.0 - u);
float sinTheta = sqrt(1.0 - cosTheta * cosTheta);
return vec3(cos(phi) * sinTheta, sin(phi) * sinTheta, cosTheta);
}
请注意,返回的方向当然是在默认的坐标框架中,并带有z-up(如果你愿意,你也可以称之为切线空间)。因此,在应用程序中可能需要执行的最后一步是通过使用由本地法向量构建的正交法向量基矩阵将返回的方向转换为世界空间。
5. 补充说明
在这里,我收集了一些关于如何使用这些点的进一步说明,以及其他一些值得了解的事情。
5.1. 这些点有多好呢
质量当然取决于应用,但首先要注意的是,对于少量的点,2D中的Hammersley点集在半球上的分布不是很好。这一点可以在一节中很容易得到验证。当需要很多点的时候,这个问题就会减轻,例如在进行交错采样的时候。虽然有许多其他的准随机序列可以使用,但到目前为止,我还没有发现任何可以像Hammeysley点集那样有效实施的序列(除了秩-1的格子,但他们不容易用于不同数量的点)。
这种采样模式的另一个问题是,在开始计算任何一个点之前,需要预先知道 N N N个点的数量。这在实时渲染应用中几乎不是问题,但一旦进行某种形式的渐进式渲染,使用一个准蒙特卡洛序列(而不是一个点集)可能是一个更好的选择。
5.2. 交错式采样
交错采样[keller01]是一个经常使用的优化方法 [segovia06] ,用于实时渲染,其中一个积分的计算被分散到几个像素上,然后在一个额外的过滤步骤中合并。
当然,任何点的集合都可以用于此,但是简单的构造和使用使它特别容易将点集合分割成几个片段和/或半球。
6. 补充原文
原文中虽然有可视化生成Hammerslep随机点的例子,但是后续解释公式的时候,并未给出详细的例子,所以此处参考低差异序列(一)- 常见序列的定义及性质补充更为详细的例子
6.1. Radical Inversion与Van der Corput序列
接下来在介绍这些序列定义之前,先介绍一个基本的运算,Radical Inversion。这篇专栏将会介绍的所有序列都会用到这个运算过程。
i = ∑ l = 0 M − 1 a l ( i ) b l i=\sum_{l=0}^{M-1}{a_l\left( i \right) b^l} i=l=0∑M−1al(i)bl
Φ b , C ( i ) = ( b − 1 . . . b − M ) [ C ( a 0 ( i ) . . . a M − 1 ( i ) ) T ] \varPhi _{b,C}(i)=\left( b^{-1}...b^{-M} \right) \left[ C\left( a_0\left( i \right) ...a_{M-1}\left( i \right) \right) ^T \right] Φb,C(i)=(b−1...b−M)[C(a0(i)...aM−1(i))T]
这个操作非常直观, b b b时一个正整数,则任何一个整数 i i i,如果先将 i i i表示成 b b b进制的数,然后把得到的数中的每一个位上的数字 a l ( i ) a_l(i) al(i)排成一个向量,和一个生成矩阵(genetator matrix) C C C相乘得到一个新的向量,最后再把这个新向量中镜像到小数点右边去就能得到这个数以 b b b为底数,以 C C C为生成矩阵的radical inversion(基数逆) Φ b , C ( i ) \varPhi_{b,C}(i) Φb,C(i)
上面的描述可能略微有些复杂,但如果矩阵 C C C是单位矩阵(Identity Matrix)的时候,这个过程会简化很多,即是直接把这个 b b b进制数镜像到小数点右边去即可。同事也是Van der Corput序列的定义。
Φ b , C ( i ) = ( b − 1 . . . b − M ) ( a 0 ( i ) . . . a M − 1 ( i ) ) T = ∑ l = 0 M − 1 a l ( i ) b − l − 1 \varPhi _{b,C}\left( i \right) =\left( b^{-1}...b^{-M} \right) \left( a_0\left( i \right) ...a_{M-1}\left( i \right) \right) ^T=\sum_{l=0}^{M-1}{a_l\left( i \right) b^{-l-1}} Φb,C(i)=(b−1...b−M)(a0(i)...aM−1(i))T=l=0∑M−1al(i)b−l−1
举个例子,正整数8以2为底数的radical inverse的计算过程如下,首先算出8的2进制表示,1000。此处假设 C C C为单位矩阵,所以直接将1000镜像到小数点右边,0.0001.这个二进制数的值就是最终结果,把它转换回10进制就得到1/16,既 Φ 2 ( 8 ) = 1 16 = 0.0625 \varPhi_2(8)=\frac{1}{16}=0.0625 Φ2(8)=161=0.0625。下面的表给出了更多的以2为底数的Van der Corput序列的例子。
| i i i decimal | i i i binary | Φ 2 ( i ) Φ_2(i) Φ2(i) binary | Φ 2 ( i ) Φ_2(i) Φ2(i) decimal |
|---|---|---|---|
| 0 | 0000.0 | 0.0000 | 0.0 |
| 1 | 0001.0 | 0.1000 | 0.5 |
| 2 | 0010.0 | 0.0100 | 0.25 |
| 3 | 0011.0 | 0.1100 | 0.75 |
| 4 | 0100.0 | 0.0010 | 0.125 |
| 5 | 0101.0 | 0.1010 | 0.625 |
| … | |||
| 11 | 1011.0 | 0.1101 | 0.8125 |
| … | |||
Van der Corput序列有几个属性:
- 每一个样本点都会落在当前已经有的点里"最没有被覆盖"的区域。例如 Φ 2 ( 3 ) = 3 4 \varPhi_2(3)=\frac{3}{4} Φ2(3)=43时刚好落在了 [ 0 , 1 ) [0,1) [0,1)区间中被覆盖最少的区域( Φ 2 ( 0 ) = 0 , Φ 2 ( 1 ) = 1 2 , Φ 2 ( 2 ) = 1 4 \varPhi_2(0)=0,\varPhi_2(1)=\frac{1}{2},\varPhi_2(2)=\frac{1}{4} Φ2(0)=0,Φ2(1)=21,Φ2(2)=41)
- 样本个数到达 b m b^m bm个点时对 [ 0 , 1 ) [0,1) [0,1)会形成uniform的划分。例如 Φ 2 ( 0 ) = 0 , Φ 2 ( 1 ) = 1 2 , Φ 2 ( 2 ) = 1 4 , Φ 2 ( 3 ) = 3 4 \varPhi_2(0)=0,\varPhi_2(1)=\frac{1}{2},\varPhi_2(2)=\frac{1}{4},\varPhi_2(3)=\frac{3}{4} Φ2(0)=0,Φ2(1)=21,Φ2(2)=41,Φ2(3)=43
- 很多时候并不能代替伪随机数,因为点的位置和索引有很强的关系,例如在以2为底的
Van der Corput序列中,索引为奇数时候序列的值大于等于0.5,偶数时则小于0.5
6.2. 使用Hammersley产生随机数的伪代码
产生二维随机数,效率较高
// 此处以2为底数产生二维随机数所用,直接用位操作效率极高,如要拓展到多维,则看下一种做法
float RadicalInverse_VdC(uint bits)
{
bits = (bits << 16u) | (bits >> 16u);
bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);
bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);
bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);
bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);
return float(bits) * 2.3283064365386963e-10; // / 0x100000000
}
// ----------------------------------------------------------------------------
vec2 Hammersley(uint i, uint N)
{
return vec2(float(i)/float(N), RadicalInverse_VdC(i));
}
const uint sample_count = 1024u;
for(uint i = 0u; i < sample_count; ++i)
{
Vector2f u_v = Hammersley(i, sample_count);
.....
// random_x = u_v.x;
// random_y = u_v.y;
}
扩展到多维
// 0.35
double make_hammersley_sequence(int index, int base) {
double f = 1, r = 0;
while (index > 0) {
f = f / base;
r = r + f * (index % base);
index = index / base;
}
return r;
}
void hammersley_random()
{
for (uint i = 0u; i < max_num; ++i)
{
draw_points.emplace_back(float(i) / float(max_num), make_hammersley_sequence(i, 2));
// 三维
draw_points.emplace_back(float(i) / float(max_num),make_hammersley_sequence(i, 2)
, make_hammersley_sequence(i, 3));
}
}
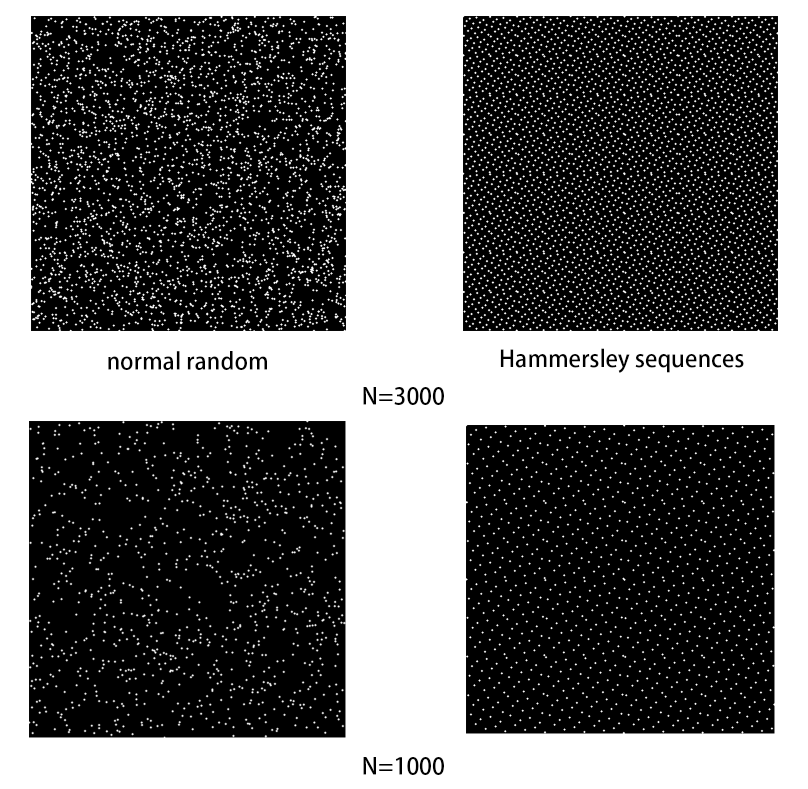
6.3. 效果对比图
可以看到Hammersley序列比c++自身标准库的random实现更加的分布均匀
翻译自:http://holger.dammertz.org/stuff/notes_HammersleyOnHemisphere.html
引用博客:
可拓展阅读: