目录

1. DTFT 的定义式
DTFT(离散时间信号傅里叶变换):一个在时域内不连续的信号 被使用
来表示,即一个函数可以表示为级数表达式

当得知频域内的信号表达式时,使用下面的方法来表示时域信号,即为傅里叶反变换:

可以认为,反变换定义式使得任何序列可以被分解为指数序列 的加权相加
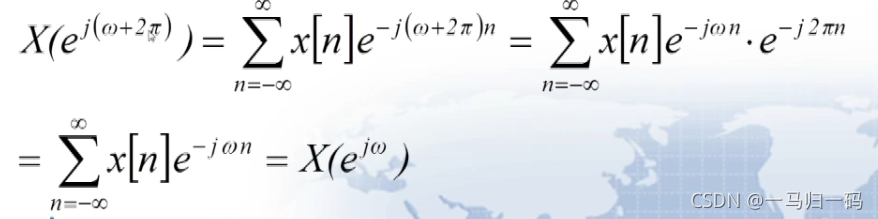
2. DTFT 的性质
(1)周期性

可以看出,经过 DTFT ,信号为周期函数,其周期为 2pi ,傅里叶级数的系数为 x[n], 即累积的级数的权值;一般来说由于其周期性,我们研究的过程中关注的多是其一个周期内部的变化
(2)复数特性
一般来说,经过 DTFT 得到的 X(e^(jw))是复数形式,可以使用下面的式子表示:

也可以使用极坐标来表示:

可以看出极坐标形式的变换包括幅度值和相位,都和原来的式子有关

上图中表示,相位函数并不是唯一的,经过 2pi 的周期后相位函数还是和原来的函数一样,所以一般将相位角约束在 [-pi,pi]之间
(3)共轭对称性

一般经过离散时间傅里叶变换后变为如上所示的复数函数

可以看出原序列的偶部对应变换后的函数的实部,原函数的奇部对应变换后的函数的虚部 ,那么是什么原因造成这种情况呢
是因为满足共轭对称性:

即实部(幅度)为一个偶函数,虚部(相位)为一个奇函数
(4)收敛性

定义式在数学表达式上是一个无穷级数和,所以在收敛方面存在问题
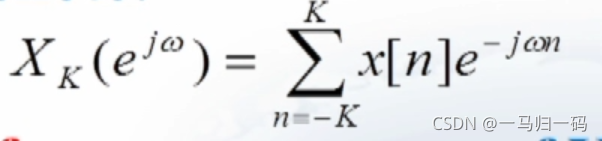
当级数求和的范围取为有限的时,该级数肯定收敛,收敛方式主要有以下两种:
a: 一致收敛

即当 K 趋于无穷大时,两函数的误差趋近于 0
b:均方收敛

即误差的模的平方随着K的增大在一周内趋于0
当原序列 x[n] 绝对可求和时一定可以使变换收敛,即:
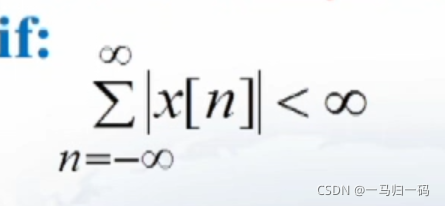


所以也可以说,序列绝对可求和是 DTFT 存在的充分条件,由上图可知,绝对可求和的序列一定属于平方可求和,即绝对可求和强于平方可求和
(5)线性性质

时域的线性组合在频域也满足相应的组合
可以使用定义式进行证明
(6)反折性质
时域取反,那么频域也可以取反

(7)时移性质

将原信号在时域进行移动,那么在频域内相位发生变化
(8)频移性质

在频域内对该信号进行搬移,那么在时域内就是对其乘以一个指数量,可以从定义式进行推导
(9)频域微分性质

时域内对信号乘以时域变量 n ,那么频域内对频谱求导再乘以 j
(10)卷积性质
时域内两信号相卷,在频域内可以理解为两个信号相乘,可以将卷积运算转化为傅里叶变化后的乘积运算

(11)调制性质
时域相乘,频域相卷

由于频域内是周期函数,所以卷积运算过程中的积分范围为一个周期
(12)帕塞瓦尔关系式

3. 性质的应用
(1)卷积性质的应用

时域内相卷的运算,需要大量的运算量,将其转化为频域内的相乘,可以简化运算
(2)频移性质的应用

计算 y[n] 的 DTFT ,首先将其转化为常见的序列,再通过频移性质以及常见序列的变化获得结果
(3)线性性质和频域微分性质的应用

计算 y[n] 的 DTFT ,首先通过线性性质将其转化为较为简单的和的性质,通过频域微分性质和常见序列的应用得到转化后的频域表达式
(4)帕塞瓦尔关系式的应用


计算 h[n] 的 能量,使用帕塞瓦尔表达式将其能量通过频域一个周期内的积分计算出来
由于信号频域幅度的平方代表序列的能量在频域内的分布规律,所以幅度谱平方定义为能量谱密度函数