用数学方法计算井字棋合法局面数——波利亚定理的简单应用

0.前言

记不得那天在B站发现一个互动下井字棋智商普查(BV1JE411G71J)，想当年被小学同学评价为无敌破战士(显然到现在都不知道这称号是啥意思)的我义无反顾的点了进去，~~然后获得了满盘皆输的好成绩~~。正好想到之前晚四晚五学习的波利亚定理都没怎么用过，于是就想了这么个题，经过两个星期的自闭之后，就有了这篇文章。

注:本文大部分内容仅需要小学二年级学历(涉及乘法的计算)。

1.常规做法

此部分需要一定的计算机基础，如果您小学一年级没有选修计算机的话，记住答案是765，跳过即可。

什么，你还想问为什么是765？没关系，满足你。

棋谱1

棋谱2

棋谱3

数数看，应该是765个。满意了吧。

如果您学过一点算法，不难想到，这个题可以直接dfs。

但是要注意棋盘有对称性，所以每种搜到的情况都要存入所有的对称。

由于作者几百年没碰C++，所以这里直接上Python代码。

cnt = 0  # 合法局面数
results = {
    
    }  # 所有可能局面，不考虑对称
ans = []  # 本质不同的局面


def dfs(state, cur):  # 局面状态，目前落子方
    global cnt, results, ans
    if tuple(state) in results.keys():  # 记忆化
        return
    cnt += 1
    ans.append(tuple(state))
    ex_states = ex(state)
    for ex_state in ex_states:
        results[tuple(ex_state)] = True  # list不能做字典的键，使用tuple转化
    if is_win(state):  # 胜利即返回
        return
    for i in range(0, 9):  # 落下一颗子
        if state[i] == 0:
            state[i] = 1 if cur else 2
            dfs(state, not cur)
            state[i] = 0


def ex(state):  # 获取所有对称
    ex_states = []
    ex_strategys = [[0, 1, 2, 3, 4, 5, 6, 7, 8],
                    [2, 1, 0, 5, 4, 3, 8, 7, 6],
                    [6, 7, 8, 3, 4, 5, 0, 1, 2],
                    [8, 5, 2, 7, 4, 1, 6, 3, 0],
                    [0, 3, 6, 1, 4, 7, 2, 5, 8],
                    [6, 3, 0, 7, 4, 1, 8, 5, 2],
                    [8, 7, 6, 5, 4, 3, 2, 1, 0],
                    [2, 5, 8, 1, 4, 7, 0, 3, 6], ]  # 数字代表对称后的元素号
    for strategy in ex_strategys:
        ex_states.append(rearrange(state, strategy))
    return ex_states


def is_win(state):  # 判断是否胜利
    win_strategys = [[0, 1, 2], [3, 4, 5], [6, 7, 8],
                     [0, 3, 6], [1, 4, 7], [2, 5, 8],
                     [0, 4, 8], [2, 4, 6]]
    for strategy in win_strategys:
        if is_equal(state, strategy):
            return True
    return False


def rearrange(a, arrange):  # 按照arrange数字顺序重排
    ret = []
    for i in arrange:
        ret.append(a[i])
    return ret


def is_equal(a, indexes):  # 判断对应位置上是否相等
    for i in indexes:
        if not a[i] or a[i] != a[indexes[0]]:
            return False
    return True


def print_state(state):  # 输出局面
    model = "{0[0]} | {0[1]} | {0[2]}\n—————————\n{0[3]} | {0[4]} | {0[5]}\n—————————\n{0[6]} | {0[7]} | {0[8]}"
    temp = []
    for i in state:
        if i == 0:
            temp.append(" ")
        elif i == 1:
            temp.append("O")
        else:
            temp.append("X")
    print(model.format(temp))


if __name__ == "__main__":
    dfs([0, 0, 0, 0, 0, 0, 0, 0, 0], True)  # O先手
    print(cnt)
    for i in range(0, len(ans)):
        print("#%d:" % (i + 1))
        print_state(ans[i])

原理十分简单，用不了1s就能出答案(不包括输出用时)。

但是你再仔细想想，在遥远的公元前1世纪，连电脑的影子都没有，你要是穿越回去了，就没东西跑你的迪法师了。~~(强行解释)~~

再说了，毕竟不是人人都会在代码之田上殷勤的耕耘，这就回到了本文的标题：用数学方法计算。

2.基本计数思路

我们会发现，直接求解这个问题会显得比较复杂。俗话说得好，正难则反，这里咱们就采用这样的计数思路。

为了方便计数，我们规定O先手。我们可以先不考虑任何的输赢情况，仅仅计算所有符合双方轮流下子条件的所有局面(即双方都不下、1个O、1个O和1个X、2个O和1个X，以此类推)，在此基础上，我们再减去所有的非法局面(即决出胜负后双方仍在下棋，如下图，显然O已经取得了胜利，而X还在下，合法局面下应该只有2个X，因为O先手)，这样我们就得到了所有合法的局面数了。

非法局面

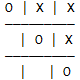
那么你可能会想了，一般的计数原理可以解决吗？

显然不大行，注意到棋盘可以旋转、可以翻转，这些局面在本质上都是相同的。我们称这些不引起棋盘本身发生变化的置换(即操作)为对称。显然，一个构型(即图形)拥有的对称越多，它就越对称。比如你看正方形可以有不动、顺时针转90°、顺时针转180°、顺时针转270°、绕2条对称轴翻折、绕2条对角线翻折这么多可以让正方形本身不发生变化(即正方形还是原来的放法，并没有放歪掉)的对称，所以正方形看起来就会比较有对称美。

对于这种有对称性的构型(即图形，如棋盘、苯环等)，我们有一妙招——波利亚计数定理。

3.波利亚计数定理的应用

此部分主要教你简单的应用波利亚定理。关于波利亚定理的内容及证明，限于篇幅有限，此处不做赘述。想体验自闭的快乐的读者可自行查找。

让我们先来看一个简单的问题：求甲苯的二氯代物个数。

为了方便起见，我们将甲苯上的空余碳位标号，用蓝线画出其对称轴。

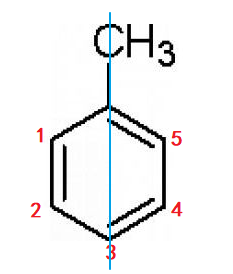
由于甲苯没有旋转对称性，所以我们仅需考虑轴对称。那怎么描述一个对称呢？

我们对比对称前后的图形，不难发现，对称前后1、5，2、4位置发生调换，3位置不动。我们采用如下记法：

(1 5)(2 4)(3)

将发生调换的两个位置按照先后顺序(对称前、对称后)写在一个括号内，不变的位置单独写在一个括号内。

然后呢？定理要求我们计算括号内的所有数字代表意义都相同的情况数，比如(1 5)即是1、5位置要么都不放Cl，要么都放Cl。掰手指可得，这样的情况有2种：1、5放Cl，2、4放Cl。

接着，用情况数除以对称数即是答案。这里有一种对称，所以答案就是2。

等等，这答案不对啊！

你仔细想下，其实这样就漏了一种最基本的对称：不动。仿照上面的写法，应写为：

(1)(2)(3)(4)(5)

这又有几种情况呢？5选2，共10种。算上刚刚2种，总共12种。除以总对称数2，答案是6。

再考虑一个简单的问题：求对二甲苯的二氯代物个数。

同样，我们标出空余碳位号，画对称轴，不同的是，它有旋转对称性，我们画上旋转方向。

对二甲苯

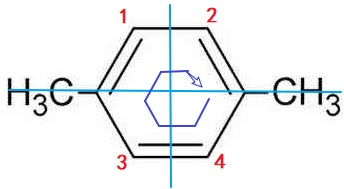
以同样的方式，让我们表示出不动和轴对称：

(1)(2)(3)(4) (1 2)(3 4) (1 3)(2 4)

我们可以采用这样的方式来表示旋转对称：(起始位置旋转1次位置旋转2次位置旋转3次位置 …… 旋转n次位置)

括号里不用出现重复数字，写出一个循环就可以了。

像这里，我们可以这样写:

(1 4)(2 3)

为什么呢？对二甲苯一次要转180°才能保证它两个-CH3在两边、形状不变，在一次180°旋转后，我们发现1转到4上，再转，4又转回1，1->4->1->4->……我们只用从头取其中一个循环1、4，写入括号即可。2、3类似。

下面让我们来计算。对 (1)(2)(3)(4) ，4选2得6；对 (1 2)(3 4) (1 3)(2 4) (1 4)(2 3)，每一个都又前一个括号、后一个括号放Cl两种选法，2*3=6。所以最后答案就是(6+6)/4=3

如果这时候，我让你算3Cl代物呢？再算一遍？

如果问题简单得话，再算一遍倒也无妨。但是对于对称更多的图形，再算一遍显然很不尽人意。有没有一劳永逸的方法呢？

显然有的。仔细看看刚才的计算过程，你会发现其实答案只是和括号个数、括号内数字个数有关，并不会关心括号里是几。基于这一点，我们可以根据这些对称来构造出这样一个多项式(即圈指标)：

$1/4*((a+b)^4+3(a^2+b^2)^2)$

前面的系数为1/对称数，括号内的每一项根据我们描述的每一个对称改写而来：如果括号内有n个数，那么对应的括号内的所有字母都是n次的，括号内的字母代表了当前位置上的状态(比如此处a，b分别代表放Cl，不放Cl，有几个状态就有几个字母)，接着，把所有对应括号相乘，即可得到该对称对应的代数表达。具体来说，对于**(1 2)(3 4)**这个对称，我们有两种状态，记作a，b，括号内有两个数字，所以a，b为2次，一个括号可以写为 $a^2+b^2)$ ，两个括号相乘，即是 $a^2+b^2)^2$ 。在此基础上，把所有的对称相加，乘上系数就得到了我们这个多项式。

把多项式展开，我们得到：

$b^4+ab^3+3a^2b^2+a^3b+a^4$

什么意思呢？ $a^mb^n$ 前系数代表m个a状态，n个b状态的本质不同的情况数。如本例中， $3a^2b^2$ 代表了2个位置不放Cl，2个位置放Cl共有三种情况，也就是我们刚刚计算得到的二氯代物个数。

小结一下，求对称构型计数问题大致有以下步骤：

1.编号。将有关位置进行编号。

2.寻找对称。根据图形性质来寻找。

3.改写对称。将对称改写为数字、括号组合形式。

4.构造多项式。根据对称数、对称类型写出对应的多项式。

5.展开多项式，寻找计数目标，完成计数。

以上就是波利亚定理的运用了，大家学废了吗？

~~好懂么？宿舍违纪换的。~~

4.计数部分一——所有局面

此部分的目的是运用波利亚定理计算所有符合棋子个数的局面个数。

依照上文的步骤，我们对棋盘进行基本的处理：

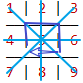
在此基础上，我们写出它的所有对称：

(1)(2)(3)(4)(5)(6)(7)(8)(9) 不动

(1 3)(2)(4 6)(5)(7 9)(8) 关于2-8轴对称

(1 7)(2 8)(3 9)(4)(5)(6) 关于4-6轴对称

(1 9)(2 6)(3)(4 8)(5)(7) 关于3-7轴对称

(1)(2 4)(3 7)(5)(6 8)(9) 关于1-9轴对称

(1 3 9 7)(2 6 8 4)(5) 顺时针旋转90°

(1 9)(2 8)(3 7)(4 6)(5) 顺时针旋转180°

(1 7 9 3)(2 4 8 6)(5) 顺时针旋转270°

同时，我们定义三个状态：

a：该格为O b：该格为X c：该格为空

根据上述准备工作，我们可以轻松构造多项式：

$1/8((a+b+c)^9+4(a^2+b^2+c^2)^3(a+b+c)^3+2(a^4+b^4+c^4)^2(a+b+c)+(a^2+b^2+c^2)^4(a+b+c))$

展开，我们可以得到如下结果：

$c^9+3bc^8+3ac^8+8b^2c^7+12abc^7+8a^2c^7+16b^3c^6+38ab^2c^6+38a^2bc^6+16a^3c^6+23b^4c^5+72ab^3c^5+108a^2b^2c^5+72a^3bc^5+23a^4c^5+23b^5c^4+89ab^4c^4+174a^2b^3c^4+174a^3b^2c^4+89a^4bc^4+23a^5c^4+16b^6c^3+72ab^5c^3+174a^2b^4c^3+228a^3b^3c^3+174a^4b^2c^3+72a^5bc^3+16a^6c^3+8b^7c^2+38ab^6c^2+108a^2b^5c^2+174a^3b^4c^2+174a^4b^3c^2+108a^5b^2c^2+38a^6bc^2+8a^7c^2+3b^8c+12ab^7c+38a^2b^6c+72a^3b^5c+89a^4b^4c+72a^5b^3c+38a^6b^2c+12a^7bc+3a^8c+b^9+3ab^8+8a^2b^7+16a^3b^6+23a^4b^5+23a^5b^4+16a^6b^3+8a^7b^2+3a^8b+a^9$

什么，你说这不得算死？没关系，给你推荐一个法宝：表达式计算器

得到计算结果后，让我们来寻找计数的目标。

我们要求符合棋子的个数，由于是O先手，所以会有这么几种符合条件的棋子个数：

不下、1个O、1个O和1个X、2个O和1个X、2个O和2个X、……、4个O和4个X、5个O和4个X

按照我们规定的状态，上述文字表达可以改写为：

$c^9、ac^8、abc^7、a^2bc^6、a^2b^2c^5、a^3b^2c^4、a^3b^3c^3、a^4b^3c^2、a^4b^4c、a^5b^4$

$c^9$ 即9个空格，也就是不下； $ac^8$ 即1个O和8个空格，也就是下1个O；其余以此类推。

从上述结果中，我们可以找到每一项对应的系数：

1、3、12、38、108、174、228、174、89、23

把它们加起来，可以得到所有符合棋子个数条件的局面数：

1+3+12+38+108+174+228+174+89+23=850

简简单单完成第一步。

5.非法局面判定

按照我们既定的计数步骤，现在需要算得所有的非法局面数。

在计算之前，让我们来分析一下怎样的局面是非法的。

你可能又要问了，这有什么好分析的？不就一个人赢了，另一个人只要再下就肯定非法了嘛。

按照这个想法，下面这个局面就是非法的。

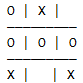
伪非法局面

显然啊，O都赢了，它干嘛还要在1位下子呢？是吧。

按照这样的道理，只要在胜利局面基础上继续下棋的，都是非法的。

我最开始也是这么想的。这条路走下去，我成功的自闭了两个星期。

你再仔细想想，上面这个局面，真的是非法的吗？

你觉得这个局面对于O来说，只有一种下棋方法吗？难道所有的局面的下法都像你一样有智慧，一定是先下那连着的3个O吗？

换言之，O要是先下1、4、5位，与此同时，X下7、2、9位，然后O最后下6位，啪，赢了。显然，在这种下法下面，此局面合法。

你会发现，一个看似非法的局面，通过调整下棋次序，可以使之变得合法。

那你又要问了，到底什么样的局面是真正非法的呢？

从O胜利的情况入手，如果当前局面上O有3个，正好排成一线，而X只有2个的话，显然，在O胜利后X并没有再落子，否则X的个数应该是3个。反过来，如果仅有3个O排成了一线，而X有3个，无论O怎样调整它的下棋策略，都无法避免在胜利后X再落子的命运。推而广之，如果场上有n个O，因为O先手，故此时可能的X数为n或n-1，如果X有n-1个，可以理解为先让X下n-1(O先手，如果最后一步是O下的话X显然要少1个)个子，O再下n个子，在O下完后X不再下，所以O有办法通过调整自己的下棋次序来使自己在最后一步赢，然而X在O胜利后不再落子，满足一方胜利另一方停止下棋的要求；相反的，如果X有n个，即意味着在O胜利后X又下了一步，也就不符合胜利后另一方停止落子的要求了。

同样的，对于X胜利的情况，如果O数量与X一样多，就说明O在X胜利后不再落子，而O数量比X数量大的话即意味着O在X胜利后又落了一子，显然非法。

你可能还有疑问：如果O利用5子构成了双赢，这要不要去掉呢？

双赢局面

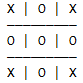
其实这也可以通过调整O的下棋顺序来使之变得合法：O先下2、4、6、8，最后一步下5，完成双赢。

小结一下，如果O胜利，O、X数量相等的局面即是非法局面；如果X胜利，O比X数量多1的局面即是非法局面。

明白了双赢局面的判断方法后，就可以着手计算了。

~~感谢颁奖典礼让我找到了判定方法。~~

6.计数部分二——非法局面

既然是对于胜利局面而言的，我们就在胜利的棋盘上计数。

为了便于利用上文做好的准备工作，我们任然采用1-9编号，并去掉不能落子的编号。

由于上文的所有局面是本质不同的，所以在处理非法局面时，我们可以令棋盘朝某个特定的方向放至，并规定1、2、3，4、5、6和1、5、9相同即胜利，在这样的规定下，诸如7、8、9，3、5、7等胜利都可以通过上述三个胜利方式进行旋转翻折得到，其本质是相同的。

由于O、X在胜利的取得上是等地位的，所以我们统一用Δ代表胜利的一方。

这样，我们得到以下3个棋盘：

胜利棋盘

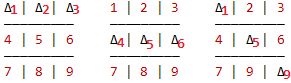
实际的能落子的只有6个格子。如果我们要表示O胜利，对于这6个格子来说，O的个数就会少3个，同样的我们也能表示X胜利。

那对称怎么写呢？我们可以利用刚刚写成的8个对称，去掉含Δ的括号，因为括号内一旦含有了不能放子的位置，就不能完成对称，因为对称过去后Δ被别的子占领，棋盘形状就发生改变。同时，如果括号内既有Δ又有正常棋位，这样的对称就无法完成，需要舍去。

按这样的道理，我们依次分析这3个棋盘的对称和多项式(圈指标)：

第一个棋盘：

(4)(5)(6)(7)(8)(9)

(4 6)(5)(7 9)(8)

$1/2*((a+b+c)^6+(a^2+b^2+c^2)^2*(a+b+c)^2)$

第二个棋盘：

(1)(2)(3)(7)(8)(9)

(1 3)(2)(7 9)(8)

(1 7)(2 8)(3 9)

(1 9)(2 8)(3 7)

$1/4*((a+b+c)^6+(a^2+b^2+c^2)^2*(a+b+c)^2+2*(a^2+b^2+c^2)^3)$

第三个棋盘：

(2)(3)(4)(6)(7)(8)

(2 6)(3)(4 8)(7)

(2 4)(3 7)(6 8)

(2 8)(3 7)(4 6)

$1/4*((a+b+c)^6+(a^2+b^2+c^2)^2*(a+b+c)^2+2*(a^2+b^2+c^2)^3)$
接着，根据非法局面的判定方法，我们列出计数对象：

O胜利：3个O和3个X、4个O和4个X，去掉无法落子的3个O：3个X，1个O和4个X

X胜利：4个O和3个X、5个O和4个X，去掉无法落子的3个X：4个O，5个O和1个X

改写为多项式形式：

$b^3c^3、ab^4c、a^4c^2、a^5b$

展开上面三个多项式，得到对应项系数分别为：

12、16、9、4；6、8、6、2；6、8、6、2

求和，得85。850-85=765，即本质不同得合法局面数共765种。

nice

好了，本文到这里就要接近尾声了。

在做这个研究前，我想，肯定会有人觉得我这是在浪费时间。“你数这个又有什么意义呢？”

可是，你仔细想想，这何尝没有意义？巩固了波利亚定理，又锻炼了分类讨论的能力。更重要的是，我借着这次机会让更多人学会使用波利亚定理，学会了对称构型的计数。

你可以在网上搜搜，在写本文前，几乎找不到井字棋计数的数学方法。这也给了我一次开拓创新的机会。

细细品一品校长特别提名奖的获得者，他们大多数并没有做出什么拯救世界拯救宇宙的事情，他们只是留心生活，做好了一般人不想做的事情。政治老师让你看《共产党宣言》，你不想看，他看了，他得奖了；网上有为灾区小朋友撰写歌词的活动，你不参加，她参加了，她得奖了……总是这些能做好大家都不愿做的事情的人得到大家的称许。

这样想来，这样的研究，又怎么是没有意义呢？

让我们带上发现的眼睛、钻研的精神，走进生活、走向成功。

这篇文章到这里就结束了。作者写了两天，希望可以得到您的支持与鼓励。

有任何问题，欢迎在评论区进行讨论。