高数

高数
- 数列和函数极限的定义:
  - 数列:任意ε，存在N，n>N时，|x-极限| < ε
  - 函数:任意ε，存在δ，0<|x-x_0|<δ时，|f(x)-极限| < ε
  - 两者的关系:函数极限存在，数列收敛且趋向于x_0，则数列极限(以数列为自变量)存在，且和函数极限相等；数列极限存在，数列收敛且趋向于x_0，函数极限不一定存在
- 极限存在准则:
  - 夹逼定理:x0的去心领域中，g(x) <= f(x) <= h(x)，如果g(x)和h(x)的极限都为A，则f(x)的极限也为A
  - 单调有界数列必有极限
- 两个重要极限:
  - $x - > 0, s i n x / x - > 1$
  - $x->∞, (1+1/x)^x -> e$
- 两个无穷：
  - 无穷大：x->x0，函数极限趋向于无穷
  - 无穷小：x->x0，函数极限趋向于0
  - 无穷小的比较：
    - 高阶无穷小：lim β / α = 0，则β是高阶无穷小
    - 低阶无穷小：lim β / α = ∞，则β是低阶无穷小
    - 同阶无穷小：lim β / α = c，则β是同阶无穷小
    - k阶无穷小：lim β / α^k = c，则β是α的k阶无穷小
    - 等价无穷小，lim β / α = 1，则β是α的等价无穷小
- 什么是连续:
  - 对于一个函数而言，某个点上，它自变量的增量趋向于零，函数的增量也趋向于零
  - 对于一个函数而言，某个点上，它自变量的增量趋向于零，f(x+x_0)趋向于该点的函数值
  - 对于一个函数而言，某个点上，自变量趋向于这个点，函数值也趋向于这个点的函数值
  - 在每一个点上连续的函数，则为连续函数。连续《==》左连续，右连续
- 某点连续的三个条件:
  - 函数在x_0处有极限
  - 函数在x_0处有定义
  - 函数在x_0处的极限等于在该点的函数值
- 什么是间断:
  - 不满足连续条件之一的点叫做间断点
- 四种间断点:
  - 第一类间断点（左右极限都存在）：
    - 可去间断点
    - 跳跃间断点
  - 第二类间断点（左右极限不存在）：
    - 无穷间断点
    - 振荡间断点
  - 无穷间断点:极限为∞(没有定义)
  - 振荡间断点:没有极限,来回振荡
  - 可去间断点:同时存在左右极限，而且极限相同，但该点要么没有函数值，要么函数值不等于该点极限
  - 跳跃间断点:同时存在左右极限，但是极限不同
- 零点存在定理:f(x)在闭区间[a,b]上连续，f(a)f(b) < 0, 则一定存在x_0, f(x_0) = 0
- 介值定理:f(x)在闭区间[a,b]上连续，f(a) = A, f(b) = B,则对于 A<C<B, 一定存在x_0, f(x_0) = C
- 什么是可导:函数f(x)在x_0的某个领域内处有定义，在x_0处取增量Δx，得到函数值的增量Δy=f(x+x_0) - f(x)，当增量Δx趋向于0，Δy比上Δx的极限存在，则该函数在x_0处可导
- 连续和可导的关系:可导(光滑)一定连续(一笔画)，连续不一定可导
- 什么是微分:函数f(x)在x_0处去增量Δx，对应的函数值的增量Δy=f(x_0 + Δx) - f(x_0)可以表示成AΔx+o(Δx)，则f(x)在x_0处可微。其中，微分dy=AΔx
- 可微和可导的关系:可导和可微充分必要
- 什么是解析:f(x)在x_0处解析指f(x)在x_0及其领域内处处可导
- 什么是奇点:没有定义的点，如f(x)=1/x, x=0
- Riemann积分:待补充
- Lebesgue积分:待补充
- 微分中值定理
  - 费马引理(和驻点的定义):f(x)在x_0的领域U(x_0)有定义，且在x_0处可导，且f(x)>=f(x_0)(或者f(x)<=f(x_0))，则f(x_0)’=0 (通过左右导数证明)，x_0是驻点
  - 罗尔中值定理:f(x)在[a,b]连续，在(a,b)可导，f(a) = f(b)，则一定存在一点ξ∈(a,b)，使得f(ξ)’=0
  - 拉格朗日中值定理:f(x)在[a,b]连续，在(a,b)可导，则一定存在一点ξ∈(a,b)，使得f(ξ)’ = (f(b) - f(a)) / (b - a)
  - 柯西中值定理:f(x)、F(x)在[a,b]连续，在(a,b)可导，F(x)‘一定不为0，则一定存在一定ξ∈(a,b)，使得(f(b) - f(a)) / (F(b) - F(a)) = f(ξ)’ / F(ξ)’
- 泰勒公式:
  - 泰勒中值定理: f(x)在x_0处有n阶导，在x_0的领域内， $f(x)=f(x_0) + f(x_0)'/1!(x-x_0) + f(x_0)''/2!(x-x_0)^2+f(x_0)'''/3!(x-x_0)^3 + ... + f(x_0)^{(n)}/n!(x-x_0)^n + R_n(x)$
    - 带有配亚诺余项：其中 $R_n(x)=o((x-x_0)^n)$
    - 带有拉格朗日余项： $R_n(x) = f(ξ)^{(n+1)}/(n+1)!(x-x_0)^{n+1}$ ，其中 $ξ∈(x_0, x)$
      - 当n取0时，带有拉格朗日余项的泰勒公式就是拉格朗日中值定理的公式
    - 当x_0取0时：
      - 带佩亚诺余项的麦克劳林公式(x_0 = 0(在0处展开)， $R_n(x) = o(x^n)$
      - 带拉格朗日余项的麦克劳林公式 ξ=θx，Θ∈(0,1)， $R_n(x) = f(ξ)^{(n+1)}/(n+1)!(x-x_0)^{n+1} =f(θx)^{(n+1)}/(n+1)!x^{(n+1)}$
  - 拉格朗日乘子法和KTT条件:待补充
- 驻点、不可导点、拐点、极值点、最值:
  - 驻点: 一阶导数等于0的x坐标值
  - 不可导点:n阶导数没有定义的x坐标值
  - 拐点:函数的二阶导数符号发生变化的坐标值，即，凹凸性发生变化的坐标值
  - 极值点:
    - 在x_0点连续时，x_0左右函数单调性发生变化的x坐标值—>考察所有驻点和不可导点
    - 在x_0点一阶导数等于0，x_0点的二阶导数>0，极小值，否则极大值—>考察驻点处，二阶导数的正负
  - 最值:极值点、闭区间两端的点，的最大、小值
- 积分:（35页）
  - 不定积分:
    - 原函数，F(x)’ = f(x)，F(x)是f(x)的原函数
    - 不定积分，∫f(x)dx = F(x) + C，原函数的全体
  - 不定积分的求法:
    - 第一类换元: ∫f(u)u’dx ->∫f(u)du (容易提取部分到d的后面，且左边仍然存在u)
    - 第二类换元: 不容易提取部分到d的后面，选择x显式换元
    - 分部:∫vu’dx -> ∫vdu ->vu-∫udv（容易提取部分到d的后面，但左边不存在u）优先级: $e^x, sin/cosx, x^n, lnx$
  - 定积分:
    - 条件: 1. 连续，则可积或 2. f(x)在[a,b]上有界，且只有有限个间断点，则可积
  - 定积分定理
    - 积分中值定理: f(x)在[a,b]上连续，一定存在一点ξ∈[a,b]，使得 $f(ξ)(b-a) = ∫_a^bf(x)dx$
    - 牛顿莱布尼茨(定积分和不定积分的关系): 不定积分是求一个函数的原函数，定积分是求一个函数在一个区间内的面积大小。牛顿莱布尼茨公式将这两者联系了起来。
      $_a^bf(x)dx = F(b) - F(a)$
      证明: $F(b) - F(a) = F(b=x_n) - F(x_{n-1}) + F(x_{n-1}) - F(x_{n-2}) ... F(x_2) - F(a=x_1)$ ，即 $\sum_{i=2}^{n}F(x_i) - F(x_{i-1})$ ，而根据拉格朗日中值定理， $F(x_i) - F(x_{i-1}) = F'(ξ)(x_{i} - x_{i-1})$ ，所以， $F(a)=\sum_{i=2}^{n}F'(ξ)(x_i - x_{i-1})$ ，如果n趋向于∞，那么 $F(b) - F(a) = ∫_a^bf(x)dx$
      证明2:利用积分上限函数 $G(x) = ∫_a^xf(t)dt, F(x) = G(x) + C, x=a时，F(a) = G(a) + C = C，所以G(x) = F(x) - F(a)，x取b得...$
  - 定积分求法:
    - 换元
    - 分部
  - 两种反常积分:
    - 无穷限**的反常积分
    - 有穷限，但无界的**反常积分(限上无定义)
- 格林公式:待补充
- 高斯公式:待补充
- 洛必达法则:(1) x->a时，f(a)和F(a)趋向于0，(2) 在a的去心领域内，f(x)‘和F(x)‘存在，(3) lim(x->a) f(x)’ /F(x)’ 存在 ------> x->∞，略。

线代(50min)

https://www.bilibili.com/video/BV1i741157ju?p=48

线代:
- 线性方程组:
  - 概念：未知量的次数都是一次的方程为线性方程，有限个线性方程的群组为线性方程组。左边：系数矩阵；整体：增广矩阵
  - 分类：
    - 齐次线性方程组：
      - 基础解系的求法：行最简型(1. 阶梯型 2.从下往上)，同时可以得到rank®，得到r个真未知量，n-r个自由未知量…
    - 非齐次线性方程组
      - 是否有解：rank(A)?=rank(augmented matrix)
      - 通解的求法：通解=特解+导出组的基础解析
      - 求解的步骤：1.阶梯型，判断是否有解、解的个数 2.行最简型，得到导出组的基础解析 3.找到一个特解，写出通解
  - 线性方程组的三种初等变换:
    - 某一个方程的左右同乘一个非零数
    - 交换两个方程的位置
    - 方程1的倍数加到方程2上
- 特殊矩阵:
  - 方阵
    - 对角矩阵
    - 对称矩阵：任何一个方阵都可以拆成对称矩阵+反对称矩阵，A=(A+AT)/2 + (A-AT)/2
    - 反对称矩阵
  - 梯形阵（上梯形阵）：矩阵的零行在非零行的下面，非零行的第一个非零元素前面的零元素个数随着行数的增加而增多
- 矩阵的逆
  - 逆矩阵:对于方阵A，AB=BA=E，则B是A的逆矩阵，B唯一
  - 逆矩阵的四个性质:
    - A可逆，A的逆矩阵也可逆， ${A^{-1}}^{-1}=A$
    - A可逆， ${(kA)}^{-1} = 1/kA^{-1}$
    - A可逆， ${A^T}^{-1}={A^{-1}}^T$
    - A，B可逆， ${(AB)}^{-1}=B^{-1}A^{-1}$
  - 求法：
    - A^-1 = A* / |A|
    - A-1 A = E，可知A-1非零、可逆，将A-1写成初等矩阵的乘积，则P1P2…PmA=E且P1P2…PmE=A-1
  - 求解矩阵方程：
    - AX = B,A可逆。解：A-1A=E，A-1B=X
    - XA = B,A可逆。解：AA-1=E，BA-1=X
  - 矩(方)阵A可逆判断方法:
    - |A| ！= 0，则 $A^{-1}=A^*/|A|$
    - rank(A) = n
    - A=P1P2…Pn—>求矩阵的逆的一种方法:对(A|E)做初等行变换得到 $E|A^{-1}$ )（当然，如果初等行变换之后，左边的矩阵的非零行个数小于n，表示rank(A)<n，则不可逆~）
- 行列式:由归纳法定义
- 行列式的性质，记D为一个行列式:
  - D和D的转置相等
  - D的一行xk 、D的一列xk，相当于：Dxk
  - D可以沿着行、列拆开
  - 交换两行、列，D变号
  - D的一行、列加到另一行、列上，D不变
  - D两行、列相等，D=0
  - 两行、列成比例，D=0
  - D的一行、一列为0，则D为0
  - |AB| = |A||B|（书p41得证）
- 利用余子式、代数余子式对行列式展开:
  - 余子式:
    $M_{ij}是D中除去a_{ij}所在行和列剩下的元素组成的行列式$
  - 代数余子式:
    $A_{ij}=(-1)^{i+j}M_{ij}$
    D = $a_{1k}A_{1k}+a_{2k}A_{2k}+...a_{nk}A_{nk}$ ，k可以取任意列（当a中的k和A中的k不对应时，D=0）
  - 逆序数:
    γ(12345) = 0; γ(54321) = 4+3+2+1 = 10。
    $\sum_{j_1j_2j_3..j_n}{(-1)}^{γ(j_1j_2j_3..j_n)}a_{1j_1}...a_{nj_n}$
- 克拉默法则:n元一次线性方程组，如果系数行列式不等于0，则有唯一解，唯一解为（D_1/D,D_2/D,D_3/D,…）—> n元齐次线性方程组来说，D不等于0，则有唯一解，且是全零解。
- 矩阵的等价:对矩阵A做有限次初等变换得到B，则A和B等价：A≌B。 formally：B = P1P2…AQ1Q2…，P和Q是初等矩阵。 A和B等价，也就是A和B秩相同。
- 秩:
  - 定义:
    - （等价标准型）任意的矩阵都等价于一个左上角是单位矩阵，其它位置=0的矩阵，该单位矩阵的阶数就是该矩阵的秩；
    - （子式）或者说，矩阵的秩为其不为零的子式的最高阶数
  - 常见性质：
    - r（A_mxn） <= min(m,n)
    - 如果A的行列式≠0（方阵），则r（A）= n
    - max(R(A), R(B)) <= R(A,B) <= R(A) + R(B)
    - R(A+B) <= R(A) + R(B)
    - R(AB) <= min(R(A), R(B)) （向量组的线性表出）
  - 用于线性方程组是否有解的判别:
    - 普通线性方程组（ $A_{mxn}X=b$ ）:
      - 有解:rank(A) = rank(A|b) ( $b_{r+1} = 0$ )
      - 有唯一解:rank(A) = rank(A|b) =n
      - 有无穷多解:rank(A) = rank(A|b) < n
    - 齐次线性方程组：
      - 有解:一定满足
      - 有唯一解（全零解）: rank(A)=rank(A|b)=n
      - 有无穷多解（非全零解）：rank(A) = rank(A|b) < n
  - 矩阵的秩,矩阵的行向量组的秩,矩阵的列向量组的秩的关系?:把矩阵分块，得到列向量组。对矩阵做初等行变换化成阶梯式，矩阵的非零行就是矩阵的秩。而此时列向量组的秩也就是该矩阵的秩。又矩阵的秩等于矩阵的转置的秩，矩阵的转置的分块，也就是矩阵的行向量。
  - 奇异方阵/非奇异方阵：行列式为0的方阵是奇异方阵；否则是非奇异方阵；满秩《=》非奇异《=》行列式不为0《=》等价于单位阵《=》可以写成一系列初等矩阵的乘积《=》可逆
- 伴随矩阵:[[A11,A21, … An1], …[A1n,A2n,…Ann]] (其中A是代数余子式)，记作A*。AA*=A*A=|A|E；|A*| = |A|^(n-1)
- 分块矩阵：
  - 分块对角
  - 分块斜对角
  - 分块上三角
- 向量：
  - 线性组合:对于一个向量组(α1,α2,α3,…αn)，对应有一组数(k1,k2,k3,…kn)，则 $\sum_{i=1}^{n} k_iα_i$ 是线性组合
  - 向量组等价:向量组A中的每一个向量都可以被向量组B线性表出，B同理，则两者等价。其充要条件是：两个向量组所生成的向量空间是同一个
  - 线性相关:对于一个向量组(α1,α2,α3,…αn)，当 $\sum_{i=1}^{n} k_iα_i$ ，(k1,k2,k3,…kn)不是全零，则线性相关
  - 线性无关:对于一个向量组(α1,α2,α3,…αn)，当 $\sum_{i=1}^{n} k_iα_i$ ，(k1,k2,k3,…kn)全零，则线性无关
  - 1111线性关系的一些结论：
    - 线性相关的充要条件是至少有一个向量可由其它向量线性表出
    - 向量组A线性无关，加上β向量之后线性相关，则β可由向量组A线性表出且唯一
    - 向量组A线性相关，扩充至向量组B，则向量组B也线性相关
    - m个n维向量组成的向量组，秩<m，则线性相关
      - 【推论1】如果m>n，则一定线性相关
      - 【推论2】如果m=n，秩=n，也就是行列式不等于0时，线性无关
    - 线性无关向量组添加分量之后仍然线性无关
  - 极大线性无关组:对于一个向量组T=(α1,α2,α3,…αn)，存在一个线性无关的部分组，任意加入一个向量，就线性相关，则是极大线性无关组
  - 向量组秩、极大线性无关组的求法：
    - 秩的求法：将向量组按列摆，然后做初等行变换，化为阶梯式，非零行个数为秩
    - 极大线性无关组的求法：按上述操作后，每一个高度选一个，相同高度取左边
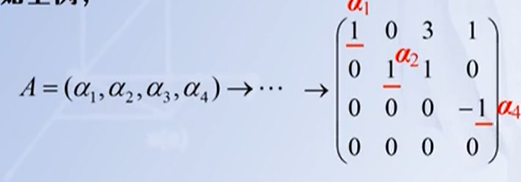
  - 向量空间:存在一个n维向量的非空集合V，如果V对加法和数乘封闭，则V是一个n维向量空间。齐次线性方程组的解集合就是这样的向量空间
    - 生成元组:对于向量空间V，存在一个向量组(α1,α2,α3,…αn)，使得V中的所有向量都可以表示为该向量组的线性组合，则V是该向量组的生成元组
    - 基:一个向量空间的线性无关的生成元组被称为基。基中向量的个数为该向量空间的维数。向量空间中的向量可以被基线性表出，对应的系数被称为该向量在这个基下面的坐标。假设一个向量空间有两组基α和β，β中每一个向量可以被α线性表出，其对应的线性方程组被称为基变换公式，其中的系数矩阵被称为过渡矩阵（β=αA）。一个向量在α下的坐标为a，在β下的坐标为b，则存在坐标变换公式（a=Ab）。
    - 如果把一堆向量看作是：
      - 集合（向量空间）：基、基的个数（向量空间的维数）
      - 向量组：极大线性无关组、无关组中向量的个数（秩）
      - 齐次线性方程组：基础解系、解系中解向量的个数
- 相似对角型：
  - 相似:
    - 概念：对于n阶方阵A和B，如果存在n阶可逆矩阵P，使得 $A=P^{-1}BP$ ，则A和B相似。
    - 性质:
      - 相似->等价
      - 如果A和B相似， $λE-A| = |λE-P^-1AP| = |P^-1||λE-A||P|$ ，则A和B有相同的特征多项式、特征值、迹、行列式、同时可逆或不可逆
    - 应用：
      - 如果V=P-1AP，则求A的k次方非常方便
  - 特征值与特征向量：
    - 概念：A是n阶方阵，a是n维非零向量，若Aa = λa，则α是A的特征向量、λ是A的特征值
    - 特征多项式：|λE-A|。A的特征值是特征多项式=0时的解，当特征值为λ1时，其对应的特征向量属于|λ1E-A|=0时的解空间
    - 性质:
      - 降秩的方阵，0一定是它的特征值。因为|A|=0，|A-0E|=0。
      - 满秩的方阵，0一定不是它的特征值。因为|A|!=0，|A-0E|=|A|!=0
      - k重根特征值所对应的特征向量个数＜k个
      - 属于不同特征值的特征向量线性无关—>A可对角化，只需要有n个不同的特征值
      - 【迹（nxn方阵的主对角元素的和称为矩阵的迹）】:特征值之和=迹。|A-λE|=(λ-λ1)(λ-λ2)…(λ-λn)。观察|A-λE|，想象成-1的逆序数次方乘xxx的和，只有当都取主对角线上元素时，可能取得λ的n-1次方，系数为-(a11+a22+…)；观察(λ-λ1)(λ-λ2)…(λ-λn)，λ的n-1次方的系数为-(特征值之和)，得证。
      - 【行列式】：特征值之积=行列式。|A-λE|=(λ-λ1)(λ-λ2)…(λ-λn)，λ取0，得证。
    - 公式：
    - 几何重数与代数重数：代数重数是某一特征值是特征多项式的几重根；几何重数是属于该特征值的线性无关向量的最大个数
    - 求法：求解特征多项式=0，得到特征值。对于一个特征值，代回特征多项式，解齐次线性方程组的基础解系（见上）。
  - 对角化:
    - 定义：方阵A和一个对角矩阵相似
    - 充要条件：
      - A有n个线性无关的特征向量
      - A的r_i重根λ_i对应的特征多项式|A-λ_iE|的基础解系有n-r_i个向量，即rank(A-λ_iE)=n-r_i
- 正交:
  - 概念：两向量内积为0
  - 正交向量组：两两正交，且不含零向量的向量组
    - 性质:
      - 正交向量组一定是线性无关的。（以两个正交向量来理解：两个向量线性无关，则不在同一条直线上，而正交是更强的一个性质，即一定垂直，所以正交必线性无关）；正交矩阵一定是可逆的。
      - 【施密特正交化】一个线性无关向量组一定和一个正交向量组等价：对于一组线性无关的向量组，可得正交化的向量 $β_1=α_1;β_2=α_2 - (α_2,β_1)/(β_1,β_1)*β_1;β_3=α_3 - (α_3, β_1)/(β_1, β_1) *β_1- (α_3, β_2)/(β_2, β_2) * β_2$
  - 正交矩阵：对于n阶方阵A，如果 $A^TA=E$ ，则A是以转置矩阵为逆矩阵的正交矩阵
    - 性质:
      - 如果A是正交矩阵，那么A的转置和A的逆都是
      - 如果存在一组标准正交向量组 $α_1,α_2,α_3,...α_n)$ ，对应的矩阵一定是正交矩阵
  - 正交变换：正交变换保证向量长度不变：Y=QX， $Y||=Y^TY=X^TQ^TQX=||X||$
- 实对称矩阵
  - 概念：略
  - 性质：
    - 实对称矩阵不同特征值的特征向量是正交的
    - 实对称矩阵k重根的特征值所对应的线性无关特征向量一定有k个
    - 实对称矩阵一定可对角化
  - 正交对角化：1.求出特征值 2.对于一个特征值所对应的特征向量，先正交化，再单位化 3.排成n阶方阵Q，使得Q-1AQ=V
- 二次型：
  - 概念：n元2次多项式：
  - 标准二次型：只含平方项
  - 二次型转换为矩阵表达式：平方项的系数直接写到对角线对应位置；交叉项的系数除以二，分别写到对称位置。得f(x1,…xn)=X^TAX
  - 矩阵表达式转换为二次型：对角线位置的元素直接作为平方项的系数；对角线以上的元素乘以二，作为交叉项的系数
  - 性质：
    - 二次型 $f(x1,..xn)=X^TAX$ ，经过可逆线性变换 $X = C Y$ 变成新变元下的二次型 $Y^TC^TACY$ ，此时 $B=C^TAC$ 也是实对称矩阵，且与和A合同
    - 二次型一定可以化为标准型：标准型的矩阵表达式就是一个对角阵，而A是一个实对称矩阵，一定和一个对角阵正交相似（合同）。故一定可以找到正交变换X=CY…。有正交变换法和配方法：
      - 正交变换法（正交）：
      - 配方法（可逆）：
    - 二次型一定可以化为规范型（系数从前到后为1、-1、0）。方法有 1. 配方法 2. 初等变换法（先对A做初等列变换，E也做；再对A做对应的初等行变换，E不做，则可将A转换为对角矩阵，E转换为转换矩阵C） 3. 求正交矩阵法
  - 二次型的分类（正定？）：
    - 正定二次型：对于任何的非零向量(x1,…xn)，二次型f(x1,…xn)>0，所对应的矩阵为正定矩阵（只对对称矩阵有定义！）
    - 半正定二次型：>=0
    - 负定二次型：对于任何的非零向量(x1,…xn)，二次型f(x1,…xn)<0，所对应的矩阵为正定矩阵（只对对称矩阵有定义！）
    - 半负定二次型：<=0
    - 不定二次型：既有>0又有<0
    - 正定的判断方法：
      - 化为标准型：f(x1,…xn)= $d_1x_1^2+d_2x_2^2+...d_nx_n^2$ ，看系数d是否全部>0
      - 看特征值是否全部>0
      - 看顺序主子式是否全部>0:
  - 惯性指数：
    - 正惯性指数：规范型中1的个数（标准型中正平方项的项数）
    - 负惯性指数：规范型中-1的个数（标准型中抚平方项的项数）
- 矩阵的合同：
  - 概念：对于矩阵A，存在可逆矩阵C，使得 $C^TAC=B$ ，则A和B合同
  - 等价、相似、合同的关系：
    - 相似-》等价
    - 合同-》等价
    - 相似和合同没有关系，当矩阵P是正交矩阵时，相似就是合同
    - 实对称矩阵一定可对角化，一定和对角阵正交相似，故和对角阵合同
- Jordan标准型
- Pseudo Inverse伪逆矩阵
- Normal Equation正规方程
- SVD奇异值分解
- PCA
- 矩阵的微分
- 矩阵的幂运算
- 齐次线性方程组:
  - n个方程+n元–>克拉默
  - 不定–>秩
- 矩阵的行列式、线性无关、秩、特征向量的几何含义:
  https://zhuanlan.zhihu.com/p/19609459
  - 行列式：NxN的行列式意味着，向量空间中，给定一组以N个极大线性无关向量组为基时，选择N个向量张成的N维广义四边形的体积
  - 线性无关和线性相关：N个向量线性无关意味着它们张成的N维广义四边形体积不为零（行列式不为零）
  - 可逆：如果一个线性变换矩阵是可逆的，那么它可以将一组线性无关的向量组映射成一组新的线性无关的向量组
  - 秩：一个线性变换矩阵的秩，就是在它的变换下，广义四边形体积不为零的最大维度
  - 特征向量：线性变换不改变它的特征向量的方向，只进行长度的改变
- 特征值、特征向量个数和秩、阶数的关系：特征值的个数=秩，特征向量的个数>=秩，特征向量的个数<=阶数。是否可对角化和是否满秩无关，当特征向量的个数=阶数时，可对角化。

概统(50min)

概统:
- 信息量:对于随机变量的某一个具体取值，衡量它发生所带来的信息量
- 信息熵:随机变量没有具体取值，衡量它的信息量，即它所有可能的具体取值的信息量的期望。熵越大，信息量期望越大，不确定性也就越大
- 一些基本概念：
  - 随机实验：满足：1. 重复无限次 2. 结果集确定 3. 下一次结果未知的实验
  - 样本空间：随机实验的结果集
  - 样本点：一次随机实验的结果
  - 随机事件：样本空间的子集
  - 事件发生：随机实验的结果落在了随机事件A中，则A发生
- 一些公式：
  - 加法公式
    - P（AUB）= P(A)+P(B)-P(AB)
    - P（AUB）=P（A）+P（B）（互不相容）
    - P（AUB）=1 - P（A逆 ∩ B逆）= 1 - （1-P（A））x（1-P（B））
- 互斥（互不相容）、对立、独立及其关系：
  - 互斥：事件A和事件B不会同时发生
  - 对立：要么事件A发生、要么事件B发生
  - 独立：事件B发生对事件A没有影响， P(AB)=P(A)P(B)
  - 关系：
    - 1. 互斥不一定对立，对立一定互斥
    - 1. 互斥一定不独立，独立一定不互斥
- 频率&概率：
  - 频率定义：随机实验E重复了n次，其中事件A发生了na次，则na/n为频率
  - 概率定义：给事件A赋予一个实数属性，满足非负性、规范型、可列可加性，则为概率
- 贝叶斯公式:
  - 定义：假设 $B_i, i= 1...n$ 是样本空间的一组完备事件，则 $p(B_i|A) = P(A|B_i) / \sum_{i=1}^{n}P(A|B_i)P(B_i)$
  - 思想：已知结果的条件下，求某一个原因的概率，可以通过已知原因得结果得条件概率以及全概率公式来替换求解
  - 应用：朴素贝叶斯算法，首先假设各个特征独立，再利用贝叶斯公式，就可以求解给定特征预测分类标签的任务，解决数据的稀疏性。
- 全概率公式:
  - 定义：假设 $B_i, i= 1...n$ 是样本空间的一组完备事件，则 $\sum_{i=1}^{n}P(A|B_i)P(B_i)$
  - 思想：达到某一结果有不同的原因，每个原因推出结果的概率都不同，求最终该结果发生的概率
- 随机变量：
  - 定义：随机实验E的样本空间为S，存在一个映射，能够把样本空间中的所有样本点都映射到一个唯一的实值，则这个映射就是随机变量
  - 伯努利试验：在同样的条件下，可以重复、独立进行的随机实验，实验的样本空间只有两个样本点：发生、不发生。
  - 分类：
    - 一维随机变量：
      - 一维离散随机变量：
        
        退化分布：
        
        两点分布：只进行一次伯努利实验，随机事件为{发生、不发生}。
        
        期望：p
        
        方差：px(1-p)
        
        二项分布：进行n次伯努利实验，随机事件为{发生的次数}。
        
        期望：np
        
        方差：npx(1-p)
        
        泊松分布：随机事件为{发生强度为λ，且独立、随机发生，则单位事件内发生的次数}
        
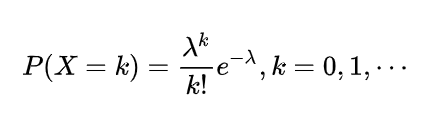
        应用：当二项分布中的n和k很大，np不太大时，可以设λ=np，用泊松分布来近似求解二项分布。二项分布描述的是在单位内个数，比如某一个时间发生的强度是λ，那么泊松分布描述的就是它在单位时间内发生次数的分布。
        
        期望：λ
        
        方差：λ
        
        几何分布：进行n次伯努利实验，随机事件为{第一次发生在第几次实验}
        
        期望：1/p
        
        方差：(1-p)/p^2
      - 一维连续随机变量：
        
        均匀分布：
        
        期望：(a+b)/2
        
        方差：(b-a)^2/12
        
        指数分布：描述泊松过程中事件之间时间间隔的概率分布
        
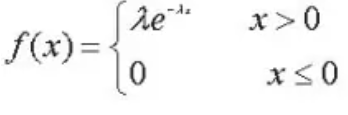
        期望：1/λ
        
        方差：1/λ^2
        
        正态分布：有很多不知什么分布的元误差叠加起来的误差的分布满足正态分布
        
        应用：用正态分布来描述一些误差的分布
        
        期望：μ
        
        方差：α^2
      - 一维随机变量的函数
    - 二维随机变量：
      - 离散：
      - 连续：
      - 独立性：联合分布函数=边缘分布函数1x边缘分布函数2
  - 性质：
    - 期望：随机变量X的取值x对应概率的求和
    - 方差：随机变量X的平方的期望-随机变量X的期望的平方
- 大数定律:
  - 伯努利:n趋向于正无穷，事件A发生的频率趋向于它的概率
  - 切比雪夫:n个不相关的随机变量，期望和方差都存在且方差是有界的，则n趋向于正无穷时，随机变量的和/n趋向于随机变量的期望的和/n
  - 辛钦:n个独立同分布的随机变量，期望为μ，则n趋向于正无穷时，随机变量的和/n趋向于μ
  - 含义：当样本容量足够大时，样本均值趋向于总体均值
- 中心极限定理:
  - 林德伯格-莱维:n个独立同分布的随机变量，期望为μ，方差为 $α^2$ ，则n趋向于正无穷时，随机变量的和~ $N(nμ，nα^2)$
  - 蒂莫夫-拉普拉斯 :n个独立同分布的随机变量，满足两点分布B(1,p)，随机变量的和~B(n,p)的二项分布，则n趋向于正无穷时，随机变量的和 $N (n p, n p (1 - p))$
  - 含义：当样本容量足够大时，样本均值的分布趋向于一个正态分布
- 期望：单个随机变量的平均大小
- 方差：单个随机变量的离散程度
- 协方差：不同随机变量之间的相关性
- 相关系数：剔除了量纲的影响。
  - 不相关，不一定独立，因为相关系数=0，E(XY)=E(X)E(Y)，推不出独立
  - 独立，一定不相关
- 常见统计量的分布:
  - 卡方分布：n个独立同分布（标准正态分布）的随机变量的加和。E=n,D=2n
  - t分布：分子是一个标准正态分布，分母是自由度为n的卡方分布除以n的开方
  - F分布：分子是自由度为n1的卡方分布除以n1，分母是自由度为n2的卡方分布除以n2
- 正态分布总体的样本统计量的分布：
  - （样本均值-总体均值）/（总体标准差/n开根号）服从标准正态分布
  - (样本方差*(n-1)) / (总体方差) 服从自由度为n-1的卡方分布
  - （样本均值-总体均值）/（样本标准差/n开根号）服从n-1的t分布
- 矩:
  - k阶原点矩:E(x^k)
  - k阶中心矩:E((x-E(x))^k)
  - k+l阶原点矩:E(x^ k y ^l)
  - k+l阶中心距:E((x-E(x)) ^ k (y-E(y))^ l)
- 区间估计：正态分布中，在给定置信水平下，通过构造样本统计量，来求得均值或者方差的置信区间
- 假设检验：正态分布中，给定原假设和备择假设和显著性水平，来构造样本统计量，根据显著性水平得到原假设的拒绝域，最后计算样本统计量的值，如果落在拒绝域里，则原假设不成立

补充

如何判断一个线性方程组的解的情况？
对它的增广矩阵化阶梯型，如果rank(增广)=rank(原)，则有解；否则无解。在有解的情况下，看rank(增广)与未知量个数的关系，如果相等，则有唯一解；否则有无穷多解。
题目：if you are given a equation like Ax=b where the column of matrix A is linearly dependent ，tell me its solution？
答案：Well，it depends on the condition of rank(A|b) == rank(A)? if it goes right, then it has solutions. In addition, because of the given condition of the column being linearly dependent, we know that rank(A)<未知量，then it has infinite solutions. Otherwise, it doesnt have any solution.
https://www.bilibili.com/video/BV1P7411C7Gz/?spm_id_from=trigger_reload
证明rank之间的关系
3.1. 证明AB=0时，r(A)+r(B)<=n：利用向量组的思想，把B看作列向量组，向量组落在了Ax=0的向量空间中，又这个向量空间的基础解系中向量的个数=n-r(A)，所以r(B)<=n-r(A)，得证
3.2 证明r(A)+r(B)>=r(A+B)：利用向量组的思想，A+B组成的列向量组中的每一个向量，都一个由(A|B)这个列向量组线性标出，所以r(A+B)<=r(A|B)，又r(A|B)<=r(A)+r(B)，得证
3.3 证明r(A)=r(ATA)：利用齐次线性方程组同解的思想
3.4 证明r(An)=r(An+1)：利用齐次线性方程组同解的思想
n阶可逆矩阵A的每行元素之和均为a，也就代表了A(全1列向量)=a(全1列向量)
矩阵之间：等价、相似、对角化、合同
矩阵自己的性质：可逆、正交、实对称、正定
假如有一枚不均匀的硬币，抛正面的几率是p，抛反面是1-p，请问如何做才能得出1/2
抛两次硬币，记录先正面后反面的次数，以及先反面后正面的次数

[数学]——一文记录高数、线代、概统知识点

目录

高数

线代(50min)

概统(50min)

补充

猜你喜欢