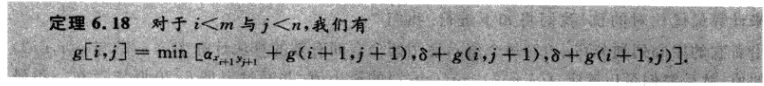前言
本文是对于算法设计的相关习题。有错误,请不吝赐教。
一、第一章
1.1 带解答的练习
1.1.1 练习1

答,我们可以通过假设一个好男人与一个坏女人约会,那么剩下的对中会存在一对坏男人与坏女人约会,此时这两对会造成不稳定性,所以在这个问题匹配问题中,每个好男人都与每个好女人约会。
1.1.2 练习2


while 存在一个自由状态的男人m
设w是男人优先级上最高的女人,还没求过婚的
if w是自由状态
if w,m 非法
m自由状态
else
m,w成为一对
endif
else
m’是w当前的约会对象
if m在w优先级中的位置高于m‘
m,w约会,m’自由状态
else
m自由状态
endif
endif
endif
把所有的约会状态改为结婚状态
类似于上述,如果存在一个不稳定因素,比如(m,w)和(m’,w’)
我们可知(m,w’)合法,且m更偏爱w’而非w,那么m一定先向w‘约会,这就产生了矛盾。
同理对应的ii,iii,以及iv等
1.2 课后练习
1.2.1 练习1

答:假,考虑两对(m,w)(m1,w1)
m 偏爱w
m1偏爱 w1
w偏爱m1
w1偏爱m
这种情况下,每个对都不是各自的第一。
1.2.2 练习2

答:真。事实上,考虑这样一个对 (m,v) 并考虑一个完美匹配包含对 (m,w’) 和 (m’,w) ,而不是(m,w).那么由于 m 和 w 都将对方排在第一位,所以在这个匹配中他们每个人都更喜欢对方而不是他们的合作伙伴,所以这个匹配是不稳定的。
1.2.3 练习3

并不是一定存在稳定的匹配,如果(30,10),(20,40)
那么就不存在一个稳定匹配。
1.2.4 练习4


答:类似于上述的算法一般:
while 存在一个医院h还有空位
设b是医院优先级上还没有询问过的最高的人
if b是自由状态
h,b成为一对
h数量-1
else
h’是b当前的约会对象
if h在b优先级中的位置高于h‘
h,b约会,h’数量+1 ,h数量-1
else
h数量不变
endif
endif
endif
1.2.5 练习5

while 存在一个自由状态的男人m
设w是男人优先级上最高的女人,还没求过婚的
if w是自由状态
m,w成为一对
else
m’是w当前的约会对象
if m在w优先级中的位置高于m‘或者=m‘
m,w约会,m’自由状态
else
m自由状态
endif
endif
endif
把所有的约会状态改为结婚状态
但是如果让n=2,让w1,为都更爱m1,而m2的选择无关紧要,那么就一定会出现一个弱匹配因素。
1.2.6 练习6


港口的优先级:船的访问次序
船的优先级:访问港口的次数(倒序)
while 存在一个自由状态的港口m
设w是港口优先级上最高的船,还没有安排过的
if w是自由状态
m,w成为一对
else
m’是w当前的约会对象
if m在w优先级中的位置高于m‘或者=m‘
m,w配对,m’自由状态
else
m自由状态
endif
endif
endif
1.2.7 练习7


这与前面的问题非常类似,输入和输出线路扮演船舶和港口的角色。一个开关精确地由输入线和输出线之间的完美匹配组成,我们只需要选择哪个输入流将切换到哪个输出线。从一个输入线的角度来看,它希望它的数据流尽可能早地(靠近源)被切换:这将在接线盒上运行到另一个已经被切换的数据流的风险降到最低。从输出线的角度来看,它希望数据流尽可能晚地(远离源)被切换到它:这最小化了撞到另一个数据strcam的风险,该数据strcam没有被切换。
优先级:遇到顺序,输入:先遇到为高,输出:后遇到为高
while 存在一个自由状态的输入m
设w是港口优先级上最高的输出,还没有安排过的
if w是自由状态
m,w成为一对
else
m’是w当前匹配的输入
if m在w优先级中的位置高于m‘或者=m‘
m,w配对,m’自由状态
else
m自由状态
endif
endif
endif
1.2.8 练习8

通过错误的优先表确实可能会得到更好的伴侣。
例子如下:

二、第二章
O(n^2)实现稳定匹配的算法:
#include<iostream>
using namespace std;
#define N 100
ManPref[N][N]
current[N]
Next[N]={
1}
WomenPref[N][N]
Ranking[N][N]
LinkList * Man;
int main(){
cin>> ManPref;
cin>> WomenPref;
init(next,current,Ranking,Man);
while(Man->next!=NULL){
int m=Man->data;
int w=ManPref[m][Next[m]];
if(current[W]==-1){
current[W]=m;
Man=Man->next;
}
else{
if(Ranking[W][m]>Ranking[w[current[w]]){
current[w]=m;
LinkList * man;
man->data=current[w];
Man=Man->next
Man->next=man;
}
}
Next[m]++;
}
return 0;
}
优先队列:
#include<iostream>
using namespace std;
#define N 100
int Heap[N];
void swap(int * a,int *b){
int * c=a,
a=b;
b=c;
}
void Heapify-up(int *Heap,i){
if(i>1){
j=Heap[i/2];
if(Heap[j]<Heap[i]){
swap(Heap[j],Heap[i]);
Heapify-up(Heap,j);
}
}
}
void Heapify-down(int *Heap,i){
int n=length(Heap);
int j;
if(2*i==n){
j=2*i;
}
else if(2*i<n){
int left=2*i;
int right=2*i+1;
j=min(Heap[left],Heap[right]);
}
if(Heap[j]<Heap[i]){
swap(Heap[j],Heap[i]);
Heapify-down(Heap,j);
}
}
int getMin(int * Heap){
return Heap[1];
}
void Insert(int * Heap,int v){
int n=length(Heap);
Heap[n+1]=v;
Heapify-up(Heap,n+1);
}
void del(int *Heap,int i){
int n=length(Heap);
Heap[i]=Heap[n];
Heap[n]=-1;
if(Heap[i]<Heap[i/2]){
Heapify-up(Heap,i);
}
else{
Heapify-down(Heap,i);
}
}
void init(){
Heap={
-1};
return Heap[N];
}
int length(int* heap){
for(int i=1;i<=n;i++){
if(heap[i] ==-1)
break;
}
return i;
}
int ExtractMin(int * Heap){
int min=Heap[1];
del(Heap,1);
return min;
}
我们可以采用优先队列来维护匹配问题中的优先表。
2.1 带解答的练习
2.1.1 练习1

f4 f2 f1 f3
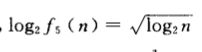
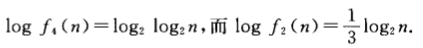
f4 f5 f2 f1 f3
2.1.2 练习2

对于常数n,可知 fn<=cgn, gn>=1/c fn,得证。
2.2 课后练习
2.2.1 练习1

2.2.2 练习2

i)6000000
ii)33015
iii) 600000
iv) 9*10^11
v) 45
vi) 5
2.2.3 练习3

f2 f3 f6 f1 f4 f5
2.2.4 练习4

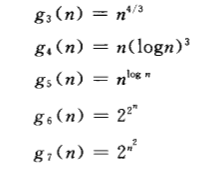
g1 g5 g3 g4 g2 g7 g6
2.2.5 练习5

a)这通常是假的
如fn=1,gn=2
b)假的。设f(n)=2n, g(n)=n为假。那么2^fn= 4 ^n,而2 ^gn = 2 ^n。
c)这是真的。因为f(n) <=cg(n)对于所有n>no,我们有(f(n)2 <c^2(g(n)) ^2对于所有n>no。
2.2.6 练习6

a)循环 n^2, 每次循环为On,所以总的为On ^3
b)精算:从1加到j 每次循环为n/2,所以最小为 n^3/32
c)
for i -1,2,n
set B[i,i+1] to A[i]+A[i+1]
for k=2,3, n-1
for i-1,2,n-k
set j=i+k
set Bpi,j] to be B[i,j-1]+A[j]
2.2.7 练习7



1+2+3+…l
2.2.8 练习8

a)我们将其放置于根号n的倍数下,首先为最高高度,然后是根号n,2根号n。。等去找到对应的值。此时每个罐子最多根号n次,总共2根号n次。
b)fn<=2kn^1/k 我们按照 n ^k-1/k的倍数来下落。
最多就是2kn^1/k次。(类似于a中的情况)
三、第三章
DFS:
#include<iostream>
#define N 100
int Discovered[N];
Queue *q;
LinkList * Graph[N];
int layerNumber=1;
void DFS(int i){
init(Graph);
push(i);
Discovered={
-1};
Discovered[i]=1;
while(q->length>0){
temp=q.pop();
LinkList * p;
p=Graph[temp]->next;
while(p!=null){
int x=p->data;
if(Discoverd[x]==-1){
push(x);
Discovered[x]=1;
}
p=p->next;
}
layNumber++;
}
}
DPS:
#include<iostream>
#define N 100
int Discovered[N];
Stack * S;
int LayerNumber=1;
LinkList * Graph[N];
void DPS(i){
init(S);
init(Graph);
push(i);
while(S->length!=Null){
int temp=pop();
LinkList *P=Graph[temp]->next;
if(Discovered[temp->data]==-1){
Discovered[p->data]=1;
}
while(p!=null){
push(p->data);
}
}
}
DFS树:
#include<iostream>
#define N 100
int Discovered[N];
Queue *q;
int Parent[N];
LinkList * Graph[N];
int layerNumber=1;
void DFS(int i){
init(Graph);
push(i);
Discovered={
-1};
Discovered[i]=1;
while(q->length>0){
temp=q.pop();
LinkList * p;
p=Graph[temp]->next;
while(p!=null){
int x=p->data;
if(Discoverd[x]==-1){
push(x);
Discovered[x]=1;
Parent[x]=temp;
}
p=p->next;
}
layNumber++;
}
}
类似的DPS树一样。
二分性测试,判断一个图是否是二部图:
#include<iostream>
#define N 100
int Discovered[N];
Queue *q;
int Parent[N];
LinkList * Graph[N];
int Color[N]={
-1}
int panduan(){
DFS();
对每条边进行遍历,看两个节点的color值是否不同
}
void DFS(int i){
init(Graph);
push(i);
Discovered={
-1};
Color[i]=0;
Discovered[i]=1;
while(q->length>0){
temp=q.pop();
LinkList * p;
p=Graph[temp]->next;
tempcolor=Color[temp];
while(p!=null){
int x=p->data;
if(Discoverd[x]==-1){
push(x);
Discovered[x]=1;
Parent[x]=temp;
}
color[x]=!tempcolor;
p=p->next;
}
layNumber++;
}
}
拓扑排序(待写):
3.1 带解答的练习
3.1.1 练习1

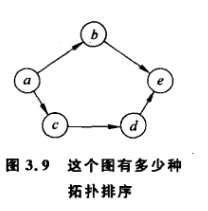
答穷举: a,b,c,d,e
a,c,d,b,e
a,d,b,d,e
3.1.1 练习2

我们考虑将一次移动看做一个节点,而机器人就是需要从a,b 节点 移动到c,d
(从一个布局中寻找)我们可以构造图H,其中节点(u,v)和(u’,v’)相连当且仅当这个布局可以连续。
我们删除H中的可能冲突节点,(距离小于等于r)
H中的节点最多为n^2个,考虑边, 每个节点都可能会有2n条边,所以共可能有 n ^3条边。

3.2 课后练习
3.2.1 练习1

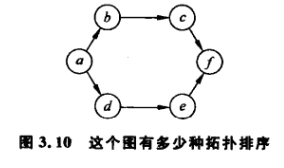
3.2.2 练习2

可以考虑BFS算法,生成一个BFS树。如果此时所有的边都在BFS树中,则G中不含有圈。如果存在边属于图G,而不属于树T,那么对应边(v,w),考虑u是v和w节点的父节点。这样们就会发现一个圈,即(v,w)边连通路径u-v和路径u-w。
3.2.3 练习3

同样采用文中的DAG算法,如果在每次迭代中都存在一个没有进入边的点,那么就存在一个DAG序列。如果在某时刻中不存在改变,那么我们就沿着其中一条边进入某个顶点v,然后沿着边遍历,直到再次遇到节点v,此时构成一个圈。
3.2.4 练习4

类似于着色问题,我们对于G中的每个节点都相连,然后通过DFS进行遍历,染色,最后对所有的边进行遍历,判断是否存在染色问题。


这个算法对于所以的边和点都遍历了一遍,所以为O(m+n)
3.2.5 练习5

树的点 n-1条,树的度为2n-2,叶节点的度 0 ,两个孩子节点的度为2,一个孩子节点的度为1。可知 n=n1+n0+n2
由度:n=n00+n11+n2*2+1
总度数为总节点数-1
3.2.6 练习6

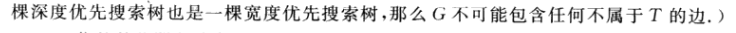
用深度优先搜索树和广度优先搜素树的结论来证明。
3.2.7 练习7

真,用图连通的度来证明。图n个点,连通,边n-1。度2n-2
每个点的度为n/2 那么一个n^2/2 >=2n-1 所以一定连通
3.2.8 练习8

假命题。(具体如下:)

3.2.9 练习9


我们假设BFS搜索从s开始,令d为层数l,必定存在一层中只有一个节点。(如果每层2个,那么2*n/2=n,而图只有n个节点所以失效。)
具体算法也如上可得。
3.2.10 练习10

BFS算法,得到每层的相应节点。倒推计算得到数量。
3.2.11 练习11


类似于染色问题我们可以考虑边,在某个时刻判断此时的感染的机器数。(m+n)
我们可以将三元组(ck,ci,tk)变为节点 ck,tk 以及ci,tk,同时采用有向边。
3.2.12 练习12

用事件来做节点,完成拓扑排序时则为一致否则不一致。
(bi节点,di节点分别代表pi的出生和死亡。
四、第四章
两种基本方法:
1.建立贪心算法领先的概念,每一步都比其他算法好
2.交换论证:考虑所有的解
1.区间调度:
贪心规则:接受结束时间最早的需求。
通过构造最优解O,并证明我们的贪心算法比最优解O做的更好。
我们需要证明对于贪心规则,他的第i个需求比最优解O中的第i个需求结束的更早。
归纳法证明:
r=1时,结论为真。
假设当r=k-1时成立。
我们证明他对r=k成立
f(j r-1)<=s(j r)
f(i r-1)<=f(j r-1)
f(i r-1) /<=s(j r)
由于选择的是集合中最小结束时间的需求,那么可知fi r<= f j r
由此也就证毕。
为何会得到最优集合呢?
假设存在一个更优秀的解O,那么|O|=m>|A|=k
那么当f jk 完成后,一定有 k+1需求存在,那么与贪心算法终止条件矛盾,
#include<iostream>
#define N 100
int f[N];
int s[N];
void A(){
init(f,s); //按结束时间排序
temp=f[0];
while(i<N){
for(int j=i.j<N.j++){
if(s[j]>=f[i]){
i=j;
break;
}
}
if(i==N){
break;
}
}
}
2.调度所有区间
资源数至少是区间集合的深度。
#include<iostream>
#define N 100
int f[N];
int s[N];
int current=0;
int A(){
int temp=0;
int Max=0;
init(f,s);//按照开始时间s来进行排序
while(current<N){
temp=0;
for(int i=0;i<current;i++){
if(f[i]>s[current]){
temp++;
}
}
temp++;
if(Max<temp){
Max=temp;
}
}
return Max;
}
3.最小延迟调度
贪心策略:最早截止时间优先
#include<iostream>
#define N 100
int d[N];
int t[N];
int f=0;
int d=0;
void A(){
cin>>s;
init(d,t);//按截止时间对需求进行排序
while(i<N){
f=s+t[i];
d+=f-d[i];
i++
}
}
我们可以很明显的看到上述算法没有空隙。
我们此处考虑一个最优调度O,然后一步步的修改它,使其保持最优性。(交换论证)
1.我们将调度O转为一个没有逆序也没有空闲的调度。此时他变为一个最优的解,有着最优的最大延迟。
补充:两个没有逆序且不存在空闲时间的调度有着相同的延迟。这种情况只可能存在于有着相同截止时间的任务安排次序不同。
所以此时这个最大延迟不依赖于这些任务的次序。
同时,当O有着逆序时,交换逆序,使其减少逆序数不会增大它的最大延迟。
4超高速缓存
最远将来规则。
证明算法的最优性。
交换论证:
考虑任意一个访问序列D,令SFF表示有最远将来规则产生的调度,S表示一个产生最小可能确实次数的调度,我们将S转换为Sff,并不增加确实次数。
我们考虑在某个数j时,有S与SFF做同样回收决定的简化操作。那么对于d=dj+1
加入此时d在超速缓存中,那么S与Sff在j+1这一步也相同。加入d需要被放入,那么S和Sff都回收相同的项,那么此时也有S=SFF
加入当回收的项不同时,加入S收回f,而SFF收回e。
我们需要将s改造为SFF。
考虑当存在一个项g不为e,f的需求,那么我们就可以让S收回e来为他留出位置
当存在需求f时,那我们收回e使其相同,如果s收回的不是e,而是e’,那我们收回e,假装将e放入。(因为不造成对应的缺页问题,所以必定存在一个最简的放入。)
此时就可以发现S与SFF相同。
由此我们可以构造最优的S*,使其第一步与SFF相同,从而得到一个完全类似的调度,并不产生更多的缺失。由此得到SFF最优。
5.最短路径:
Dijkstra:
考虑在算法执行中的任意一点的集合S,对于其中的每个点,对应的路径都是最短的S-U路径。
归纳:当s中只有一个点的时候是对的。
假设当s中k个点也正确,此时我们考虑k+1
假设下一次加入的是v,Dijkstra算法考虑到没有其他节点使得s-y-v比s-v更短。从而将v的加入集合中。(因为节点的路径非负,已经考虑过将y加入到集合,所以此时一定有x-y>u-v,所以最优。也表明了Dijkstra边值不能为负)

基于优先队列的实现:
#include<iostream>
#define N 100
PreQueue q;//优先队列,以dv为关键字
LinkList * S;
LinkList * Graph[N];
LinkList * current;
void Dijkstra(s,t){
LinkList p;
p->data=s;
S->next=p;
current=p;
int x=ExtractMain(q);
init(q);//初始化优先队列q
while(x!=t){
LinkList * temp=Graph[x]->next;
while(tmep!=null){
//修改对应的优先队列中的值
temp=temp->next;
}
LinkList *p;
p->data=x;
current->next=x;
current=p;
}
}
mlogn
6.最小生成树
1.Kruskal算法:

假设图G中的任何一课最小生成树都不含边u,v,那么将其添加到最小生成树中,此时必定含有圈,那么此时一定有另一条边(u’,v’)权值大于u,v,所以成立。
由此我们可以知道Kruskal算法和Prim算法的最优性。
(Kruskal加入边时将其中一点改为S,令另外一点为v-S,那么此时它是权值最小的边,必定包含在最小生成树中。)类似的prim也是如此,加入的点和边e都是最便宜的边。
逆删算法:
我们可以知道如下定义:

这样就直接证明了该算法的最优性。
Prim算法的实现:类似于Dijkstra算法采用优先队列,可以达到O(mlogn)的时间
7.Union-Find数据结构:
#include<iostream>
#define N 100
LinkList * S[N];
void MakeUionFind(S){
for(int i=0;i<N;i++){
S[i]->next=null;
}
}
void Union(u,v){
if(length(u)>=length(v)){
S[v]->next=S[u];
}
}
int Find(u){
LinkList * p=S[u];
while(p->next!=null){
p=p->next;
}
int x=p->data;
S[u]->next=S[x];
return x;
}
实现Kruskal算法:
#include<iostream>
#define N 100
LinkList * E[N];
LinkList *V[N];
void Kruskal(){
init(E);//对边的费用进行排序
将边e[1]的两个端点加入集合V;
for(i=1;i<n;i++){
Find(u)==Find(v)不加入
否则加入 ,然后union合并
}
}
8.聚类
对最小生成树删除k-1条最贵的边就可以得到最大间隔的k聚类
9.Huffman码与数据压缩
与最优前缀码对应的二叉树是满的。(交换论证)
假设包含一个只有一个孩子v的节点w,此时交换w和v,得到的前缀码平均位数更少。
1.自顶向下:shannon-Fano 不能保证最优
2.自底向上 Huffman编码
Huffmman算法的优越性:
我们采用归纳法:假设k-1位是最优的,那我们考虑大小为k时
ABL(T)和ABL(T’),我们可知:

于是我们假设我们贪心算法所取得的树T不是最优的,那么有着另一颗树ABL(Z)<ABL(T)

Huffman算法的实现:优先队列,关键字是字母的频率。我们只需要k次迭代,然后每次logk,所以为klogk
#include<iostream>
#define N 100
PreQueue q;
Tree Huffman(){
init(q);//初始化优先队列 ,对字母表按照出现频率排序,由低到高
for(int i=0;i<n-1;i++){
x=ExactMin();
y=ExactMin();
MakeTree(x,y);
Insert(w);
}
x=ExactMin();
return x.tree;
}
9.最小费用有向树:多阶段贪心算法
考虑之前的贪心策略,我们会发现此时生成的树并非是最小费用有向树,主要的困难点在于该树可能不是一颗有向树。
我们考虑选取其中进入v的任何边中的最小费用y,将他的其他变都减去yv。(最小生成树与边的实际费用无关。)
我们考虑选择进入v的最便宜的边的集合F,其中边可知都为0,加入F中有圈C,那么圈C中的所有边的费用都为0;因此我们将C变为一个超节点。同时将其中的每条边都进行一个替换。(将c中的边删去)
我们在这样的一张图中找到一颗相对费用的最优有向树,对于这棵树,我们将圈中除了一条边以外的其他边都加上,那么就可以将它转化为一颗G的有向树。

4.1 带答案的练习
4.1.1 练习1

我们这样证明:
归纳:当j=1时,所进行的距离比其他解更远
假设j=k成立,
我们考虑j=k+1
xpk1-xpk<=d
可知xpk>=xqk
所以组合起来可以知道
xqk-xpk-1<=d
故而能够在一天内走完xpk到xpk+1的路程,所以每天都走得更远。
因此不可能存在更小的有效停止点,所以该算法是最优的。
4.1.2 练习2

我们此处采用交换论证的方式进行证明按照递减顺序排列得到最优解:
我们假设存在一个最优解O与我们的解S不一样。
因此该最优解一定包含一个逆序。即ri<ri+1
我们将这两个交换,可得到对应的费用更低,所以算法最优。
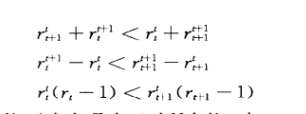
4.1.3 练习3

答:

可用割性质和圈性质来证明。
由此我们可以得出算法:通过从G中删除所有比ce大的边,删除自身,并判断改图是否有一条从v到大w的路径,当不存在时,e属于一颗最小生成树。
具体时间就是O(m+n)
4.2 课后练习
4.2.1 练习1

真。我们可知该边e是kruskal算法考虑的第一条边。
4.2.2 练习2




a):
真,改为平方后,所获得的边的顺序不变。(最小生成树与边的实际值无关,只与顺序有关。)
b):假的
假设有边(s,v),(v,t) 以及边(s,t)其费用分别为3,3,5,此时,如果改为平方,s-t最短路径就会改变。
4.2.3 练习3

归纳法:
当车数为1时,成立。
设车数为k时也成立。即此时的装的箱子大于其它算法的箱子数
当车子数为k+1时,
其它算法装上j,j+1,j+2。。。j+n
而本算法至少装上这些,所以算法最优。
4.2.4 练习4

从子序列第一个开始,从序列S中找到匹配的,然后找第二个,接着直到找完或者S遍历一遍。

这里可以通过归纳法来证明算法的最优性:
对于j=1,我们直到k1<=l1 直接寻找第一个匹配的。
同样对于j=k时成立,
那么当j=k+1时,我们找的一定是与第k+1个匹配的,而此时在找完k个后直接找,所以一定大于lk
(lk>lk-1>Sk-1)
4.2.5 练习5

从西边第一个开始,找到第一所房子,设置一个基站,删除附近所有的覆盖的房子。
归纳法证明算法的最优性。
我们算法考虑需要S集合的 s1…sk,其他的最优算法需要T集合 t1…tm
k<=m
当k对于i=1,因为我们放置第一个基站时尽可能的往东走。
我们假设对k=i成立
sk>tk
那么当k=i+1时,我们可以知道由于之前尽可能的往东走,所以sk+1 >=tk+1 位置
所以有着k<=m
4.2.6 练习6


按照后两个项目降序排列。
可知游泳池的时间是固定的。
交换证明:我们考虑其他算法必有一个逆序,bi+ri<bj+rj
那么当这两个交换时,可知后面一个人出游用时间相同,但是后面的时间变短,所以最优。
4.2.7 练习7

算法:fi的时间降序排列。
类似前面的证明。交换证明。
4.2.8 练习8

用Krusual算法,可知每次选择的都是最小的且不构成圈的边,而条件是每条边都不同,所以一定只有一颗。
4.2.9 练习9

 a) 错误 考虑(v1,v2,v3,v4)每条边vi,vj=i+j此时最小瓶颈为5,然而他的最小生成树却不是
a) 错误 考虑(v1,v2,v3,v4)每条边vi,vj=i+j此时最小瓶颈为5,然而他的最小生成树却不是
b)正确
Krusual算法,每条边都是剩下所有不构成圈中的边最小的,也就是最小的瓶颈树。
4.2.10 练习10

a)图G是邻接表表示,我们先假设将新的边e(v,w)加入到最小生成树中,我们考虑最小生成树中的v-w路径,如果该路径上的每一条边都小与ce,那么该T不变,否则T需要改变。此时只需考虑每条边即可。
b)我们考虑将最小生成树中v-w路径的权值最重的边用心的边代替,那么此时考虑其他所有的边,加入其中构成一个圈,如果加入的边为圈中最大的那条,即最小生成树成立。
证明考虑加入前的圈和,加入e后的圈,以及后续其他边加入的圈。
4.2.11 练习11

考虑一个对边而言微小的干扰因素θ,此时对于Kruskal算法而言,他的排序仍旧是相同。且也是所有生成树中最小的。所以成立。
4.2.12 练习12


a) 错误:
假设有流a,b
其中t1=t2=1,ra=r+1,rb=r-1则可以流2先走在流1.
b)
按平均的流升序排序。此时考虑每一个时刻发送的都是最小的流。如果该序列不合法,则不存在有效的调度。如果只是判断,则实际不需要排序,直接
如果要给出这个序列则需要进行排序。
(也可以考虑交换论证。)
补充: 也可以考虑松弛度降序排列
4.2.13 练习13

考虑贪心:按w/ti降序排列
可以考虑交换论证,即一定存在相邻的两项使得wi/ti<wi+1/ti+1
之前的权: witi+wi+1(ti+ti+1)
而交换之后的 wi+1 * ti+1 +wi*( ti+1 + ti)
可得交换后的值更小,所以最优。
4.2.14 练习14


a)按照进程快结束是调用,然后删除调与之重叠的进程。
结束时间升序排列。
算法的最优证明:
我们考虑其他的算法检查集合S,证明算法C,在第k个检查时覆盖的进程多与S
对于k=1,成立,
假设k=i时成立,
那么考虑k=i+1时,
可知在k=i时,p1…pm C,p1…pn 为S
那么m>=n;
因此在k=i+1时,S中必须将检查放置在pn-pl之间,
而C至少可以将检查放置在pm-pl之间,所以得到此时仍有m>n
所以成立最优。
b)这个断言是真的。我们考虑上述算法的|C|<=k*
有上述a)中的证明我们可以知道按照结束时间排序,就可以找到k个不想交的区间,此时|c|正好等于k所以成立。
4.2.15 练习15

考虑资源深度。在所有重叠区间中,我们考虑最晚终止的区间。此时一定是最优的。
可以用归纳法来证明。(考虑包含的区间)
4.2.16 练习16

按发生时间排序对xi和ti,然后遍历查找找。即考虑将xi与结束时间最早的相匹配。

交换论证,类似最远将来原则的证明,我们考虑在i之前的匹配,算法都与最优算法相同,在i+1时出现不同。
最优M将xi+1与tl匹配,
此时我们可以修改M,将其构造为贪婪算法。最优得证。
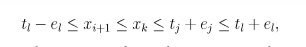
4.2.17 练习17


我们按照结束时间排序。并删除掉与其重叠的任务。
我们需要证明对于贪心规则,他的第i个需求比最优解O中的第i个需求结束的更早。
归纳法证明:
r=1时,结论为真。
假设当r=k-1时成立。
我们证明他对r=k成立
f(j r-1)<=s(j r)
f(i r-1)<=f(j r-1)
f(i r-1) /<=s(j r)
由于选择的是集合中最小结束时间的需求,那么可知fi r<= f j r
那么如果O中还存在任务r+1,那么贪婪算法中一定也能取到该任务,所以最优。
由此也就证毕。
4.2.18 练习18

最短路径问题Dijstra算法改进,我们存储下从开始节点s到达各个节点的最短路径,同时存下其中最短的,直到找到结束节点W。

可以用优先队列来存储。mlogn
4.2.19 练习19(!?)


Krusual算法,通过将边的权值改为负的带宽。(?)
4.2.20 练习20

4.2.21 练习21

五、第五章
1.对于归并排序:
我们可以知道Tn=2 T n/2+ On
那么展开可以知道第一层为cn+后续的递归调用时间
第j层也为n/2j 每层总和也为cn
所以将问题划分为2个时需要log2n次递归,因此总共为cn*logn =nlogn
我们也可以将解带入。Tn=2c(n/2)log2(n/2)+cn=cn(log2n-1)+cn=cnlog2n
2 递推为Tn<=qTn/2+cn
T2<=c
还是可以展开的方式来求解。
我们这里假设q=3
第一层就是3/2cn
第j层就是 (3/2)^k*cn
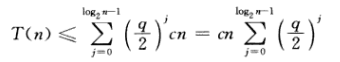
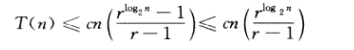
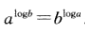
归纳总结可得
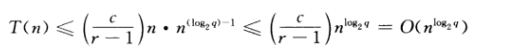
当q=1时可知为On
3.假如当组合合并所需的时间为cn2时
即递推公式为 Tn=2(Tn/2)+cn2
此时可知为O(n^2)
4.计数逆序
蛮力搜索算法为O(n^2)
这里我们考虑分治策略,将问题分为两部分。
但问题的关键是我们需要在线性时间内合并这两个部分所求得的解。
#include<iostream>
using namespace std;
int Mergecount(int *a,int * b){
int i=j=0=w;
count=0;
int * c;
while(i<length(a)&&j<length(b)){
if(a[i]>b[j]){
count+=length(a)-i;
c[w]=b[j];
j++;
w++;
}
else{
c[w]=a[i];
i++;
w++;
}
}
return count,L;
}
int sortcount(int *L){
if(length(L)==1){
return 0;
}
else{
int * a=L(0:length(L)/2);
int * b=L(length(L)/2+1:length(L));
(counta,A)=sortcount(a);
(countb,B)=sortcount(b);
(Count,L)=Mergecount(A,B);
}
return counta+countb+count,L;
}
5.找最邻近点对
考虑按照x轴排序,并将其按照x坐标分为两半
#include<iostream>
using namespace std;
int closePair(int *p){
init(px,py);//排序按照x轴,和y轴
ClosetpairRec(px,py);
}
closepairRec(int * px,int *py){
if(length(P) <3){
count(P);//计算其中最近的点对;
return (r,r2);
}
else{
init(qx,qy,rx,ry);
(q,q1)=closepairRec(qx,qy);
(r,r1)=closepairRec(Rx,Ry);
int md=min(distance(q,q1),distance(r,r1));
int x=max(q);//q中x的最大坐标
init(L);//L为q中坐标为x的点
init(S);//S为R中距离小与L为md的点的集合
init(Sy);//按照y坐标排序
while(i<15){
(s,s1)=count();//计算每个点的距离;
i++;
}
if(distance(s1,s2)<md){
return (s1,s2);
}
else if(distance(q,q1)<distance(r,r1)){
return (q,q1);
}
else{
return (r,r1);
}
}
}
Tn=2T(n/2)+On
所以也为Onlogn
6.整数乘法
我们将整数的乘法改为部分和,即将两个数分别分为高阶和低阶的两个部分,并通过相应的组合来得到最后的结果。
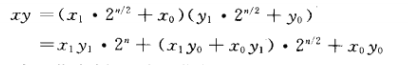
我们可以考虑(x1+x0)(y1+y0)-x1y1-x0y0 此时只需q=3
#include<iostream>
using namespace std;
int Miltiplly(x,y){
x=x1*pow(2,n/2)+x0;
y=y1*pow(2,n/2)+y1;
count(x1,x0);//计算x1+x0
count(y1,y0);
P=Militiplly(x1+x0,y1+y0);
x1y1=Militiplly(x1,y1);
x0y0=Militiplly(x0,y0);
return x1y1*pow(2,n)+(p-x1y1-x0y0)*pow(2,n/2)+x0y0;
}
7.卷积与快速傅里叶变换
卷积:
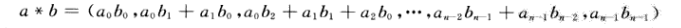
对于a有m个坐标,b有n个坐标,他们的卷积有着m+n-1的坐标
我们考虑A*B此时,对于卷积只需On,
我们考虑将A平分为两个得到如下:
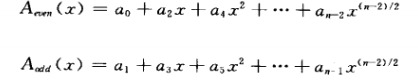
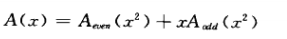
故而此时可以

wj,2n^n 是单位1的一个n次方根
我们可以用onlogn来对A,B分别求值,在On对C求值。
对于得到的2n个值我们可重新构造C,使得C为2n-2阶
构造方案:
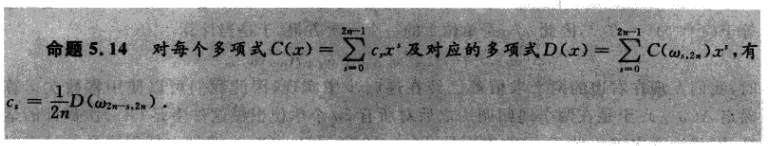
所以总的为Onlogn时间完成卷积的计算。
5.1 带答案的练习
5.1.1 练习1

由于算法的时间是Ologn,那么我们最多执行c次运算,在n/2递归下去。这就构成了对应的运行时间。
也就是Tn=T(n/2)+c
我们采用这样的算法思路:
#include<iostream>
using namespace std;
int findMidNumber(int start,int end){
if(end-start==0){
return end;
}
else{
int n=(end-start)/2;
if(number[n]>number[n-1]&&number[n]<number[n+1]){
return n;
}
else if(number [n]>number[n-1]&&number[n]<number[n+1]){
findMidNumber(n+1,end);
}
else{
findMidNumber(start,n-1);
}
}
}
5.1.2 练习2

Onlogn
Tn=2Tn/2+on
我们可以想到将时间分为两段,其中最优解要么在前一段s上,又或者在后一段s’上,也有可能在s,s’上。
这就是我们的递归思路。
#include<iostream>
using namespace std;
int findBest(int start,int end){
if(end==start){
return 0;
}
if(end==start+1){
return p[end]-p[start],pi,pj;
}
else{
int n=(end-start)/2;
x,pi1,pj1=findBest(start,n);
y,pi2,pj2=findBest(n,end);
if(x>y>pj2-pi1){
return x,pi1,pj1;
}
else if(y>x>pj2-pi1){
return y,pi2,pj2;
}
else{
return pj2-pi1,pi1,pj2;
}
}
}
5.2 课后练习
5.2.1 练习1

logn
我们需要考虑递推式 Tn=T(n/2)+c
我们想到的是二分搜索。所以类似的,我们这里也考虑这一点。
#include<iostream>
using namespace std;
int median(int n,int starta,int startb){
if(n==1){
return min(a[starta+1],b[startb+1);
}
k=n/2;
else{
if(a[starta+k]<b[startb+k]){
return median(k,starta+k,startb);
}
else{
return median(k,starta,startb+k);
}
}
}
5.2.2 练习2

Onlogn
Tn=2T(n/2)+On
我们可以修改之前的计数逆序的算法。
类似的如下:
#include<iostream>
using namespace std;
int Mergecount(int *a,int * b){
int i=j=0=w;
count=0;
int * c;
while(i<length(a)&&j<length(b)){
if(a[i]>2*b[j]){
count+=length(a)-i;
c[w]=b[j];
j++;
w++;
}
else{
c[w]=a[i];
i++;
w++;
}
}
return count,L;
}
int Merge(int *a,int * b){
int i=j=0=w;
count=0;
int * c;
while(i<length(a)&&j<length(b)){
if(a[i]>b[j]){
c[w]=b[j];
j++;
w++;
}
else{
c[w]=a[i];
i++;
w++;
}
}
return L;
}
int sortcount(int *L){
if(length(L)==1){
return 0;
}
else{
int * a=L(0:length(L)/2);
int * b=L(length(L)/2+1:length(L));
(counta,A)=sortcount(a);
(countb,B)=sortcount(b);
C=init(b);//对b中的每个都乘2;
(Count)=count(A,C);
(count,L)=Mergecout(A,B);
}
return counta+countb+count,L;
}
5.2.3 练习3

Onlogn
Tn=2T(n/2)+On
#include<iostream>
using namespace std;
int find(int start,int end){
if(end-start==1){
判断是否一样
如果一样返回其中任意一张卡,
}
else{
int n=(end-start)/2
x=(start,n);
y=(n,end);
find(start,n);
if(返回了一张卡){
test 这张卡与其他卡是否相关。
}
else{
find(n,end);
if(返回了一张卡){
test 这张卡与其他卡是否相关。
}
}
if(存在一个有着超过一半相关的卡){
return card;
}
}
}
补充: 该问题还可以在线性时间内求解:加入两张卡不匹配则丢弃,如果n是奇数,其中一张卡不匹配,将其丢掉,对于相等的则保留其中一张。
5.2.4 练习4(!*)

考虑通过卷积来完成,设置a向量为(q1,q2,qn),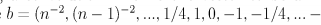
在按照对应的式子进行组合构造。构造话费n个时间。(?)
5.2.5 练习5(!*)


考虑递归Tn=2T(n/2)+On
我们按照斜率递增的方式来对直线进行标记。考虑进行分治。
当直线数量<=3条时,对应的可视关系易得。(其中中间那条只有与第一条交点在于第三条交点的左侧才是可见的)
merge 规则?
5.2.6 练习6

Ologn
意味着合并为Oc
我们这里考虑从根节点开始,如果该节点的值小与他的孩子,则返回,否则递归为他较小的子节点。
此时为logn。
证明可以通过归纳。
5.2.7 练习7(!*)

On,我们考虑递推Tn=Tn/2+ cn;
六、第六章
1.带权的区间调度:
递推:
#include<iostream>
using namespace std;
int P[N];//初始化pn使得,p[j]为它之前的一个与他不重合的任务
int V[N];
int find(int i){
if(i==0){
return 0;
}
return max(find(v[i]+find(p[i]),find(i-1));
}
备忘录形式:
此时M数组记录了之前已经算好的值。
#include<iostream>
using namespace std;
int P[N];//初始化pn使得,p[j]为它之前的一个与他不重合的任务
int V[N];
int find(int i){
if(j==0){
return 0;
}
else if (M[i]!=null){
return M[i];
}
else {
M[i]=Max(find(P[i])+v[i],find(i-1));
return M[i];
}
}
此时算法为On
如果要得到最优解,那么用M来进行追踪:
Find-Solution(int j){
if(j==0){
}
else{
if(vj+M[P[j]]>=M[j-1]){
输出j与Find-Solution(P[j])的结果
}
else{
输出Find-Solution(j-1)的结果;
}
}
}
2.动态规划原理:备忘录或者子问题迭代
我们可以使用迭代的方式来得到最优解:(在子问题上的最优解)
#include<iostream>
using namespace std;
int P[N];//初始化pn使得,p[j]为它之前的一个与他不重合的任务
int V[N];
int find(){
M[0]=0;
for(int i=1;i<=n;i++){
M[i]=max(M[P[i]]+v[i]),M[i-1]);
}
}
(允许人们从一个更小的问题中确定子问题的解)
3.分段的最小二乘:
我们从最后一个点属于最后一段考虑。那么假设最后一段为vi—vn
那么假设Opt(i-1)为前i-1个点的最优解。
那么有以下递推公式
Opt(n)=ein+C+Opt(i-1);
同样对于i-j的子问题我们也有一样的方式
Opt(j)=min(ei,j+c+OPT(i-1));(考虑最后一段的不同取值中的最小值)
由此我们建立算法:
#include<iostream>
using namespace std;
M[0]=0;
int leastSquares(){
M[0]=0;
for(int i=1;i<=n;i++){
min=0;
for( int j=0;j<=i;j++){
x=ej,i+c+M[j-1]
if(x<min){
min=x;
}
}
M[j]=min;
}
}
此时算法需要O(n3)
后面的动态规划需要On2;
对于如何获得最优的解,我们同样可以利用M数组来进行追踪。
#include<iostream>
using namespace std;
M[0]=0;
void Find(int j){
if(j==0){
}
else{
int min=0;
int mink;
for(int i=0;i<=j;i++){
int x=eij+C+M[i-1];
if(min>x){
min=x;
minj=i;
}
}
输出pminj---pj;
Find(minj-1);
}
}
4.子集和与背包
确定一个好的子问题的集合:
这里我们采用Opt(i,W)来表示对于i子问题且最大权值为w的最优解。
我们可以得到递推公式
OPt(i)=max(Opt(i-1,w),wi+opt(i-1,w-wi);
当wi>w时Opt(i)=Opt(i-1,w)
所以此处我们设计算法:
#include<iostream>
using namespace std;
int W[N];
void subsum(n,w){
for(int i=0,i<=W;i++){
M[0][i]=0;
}
for(int i=1;i<=n;i++){
for(int w=0;w<=W;w++){
if(w[i]>w){
M[i,w]=M[i-1][w];
}
else{
M[i,w]=max(M[i-1][w],M[i-1][w-w[i]]+w[i]);
}
}
}
}
类似于之前的一样,我们也可以追踪数组M来得到最优解。
背包问题:
类似的我们也可以得到相应的背包问题的解,算法基本一致。
5.RNA二级结构(区间上的动态规划)
递推式:
C[i] [j ]=max(c[i][j-1],c[i][k-1]+c[k+1][j-1]+1 )
此时k在[i,j-4]
如果此时i>j-4,C[i][j]=0;
此时算法便得到。
#include<iostream>
using namespace std;
int W[N];
void RNA(n){
for(int j=0,j<=n;j++){
for(int i=0;i<=j-4;i++){
M[i][j]=0;
}
}
for(int j=5;j<=n;j++){
for(int i=1;i<=j-4;i++){
int max=0;
int maxk=0;
for(int k=i;k<=j-4;k++){
int x=c[i][k-1]+c[k+1][j-1]+1;
if(min<x){
min=x;
minx=k;
}
}
c[i][j]=max(c[i][j-1],min);
}
}
}
}
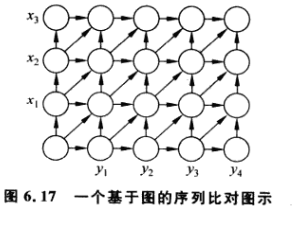
6.序列比对
我们可知一下定理正确。故而我们也就得到了对应的递推公式。

我们考虑子问题的区间为i-m 和 i,n
此时我们判断最后一个字符。
即得到OTP(m,n)=Min(OTP(m-1+n-1)+axay,OTP(m-1,n)+c,OTP(m,n-1)+c)
其中axay为错配的代价,如果此时没有错配那么为0。
由此我们可以得到我们的算法。
算法大致如下:

补充:最优比对是在对应的Gxy中的最短路径(0,0)-(m.n)
7.分支策略在线性空间的序列比对
我们可以对于上个算法的空间进行优化。我们由递推可知,每个值最多与其两列有关,故而我们通过折叠空间的方式来进行优化。
那么如何去记住我们的最优解呢,此时我们考虑上述的补充结论:即对应的最优序列比对就是图中G(0,0)至G(m,n)的最短路径。
所以我们考虑将图进行翻转,即从G[m,n]反推会G[0,0];
由此我们可以得到对应的递推公式:与之前的完全类似。
这种算法叫做逆向动态规划算法。
我们通过逆向与正向的组合使用来对算法进行优化使得空间为O(m+m),时间为O(mn).
相关算法如下:

X[q:m] ?

具体的时间证明需要考虑递推,并进行猜测替换。

8.图中的最短路径
考虑路径中可能出现负值。此时Dijkstra算法不在有效。
Bellman-Ford算法:
我们考虑Opt(n-1,s) 为s-t路径的最短路径。
考虑Opt(i,v) 他有一下两种情况:
1.v-t只需i-1条边,那么Opt(i,v)=Opt(i-1,v)
2.需要i条边,且第一条边为v-w
那么Opt(i,v)=Opt(i-1,w)+vw;
由此我们可得递推公式:
OPT(i,v)=min(Opt(i-1,v),OPT(i-1,w)+cvw);
由此我们可得相应的算法:

此时为O(n^3)
或者O(mn)对于稀疏图。
优化空间,我们考虑对于每个点值存储存储至今的最短路径。
递推式也就变为了如下:

那么如何保存最优解呢,我们可以添加first指针,用来指向对应最优路径的下一个节点。
因为对于W=first[v] 那么一定有Mv=cvw+Mw,由此可知为最优路径。此时可能出现在i次迭代后的路径长度大于i。那么我们可以考虑提前终止算法。
安全的停止算法:一次完整迭代i中没有Mv值被更新,此时可以停止算法。(?)
9.最短路径和距离向量协议
此处考虑对于Ford算法的改进,以使其更好的适合于路由器。
这就就考虑到了上节所提到的终止条件。

我们可以利用活跃节点来再度优化这个算法。

10.图中的负圈:
确定一个图G中是否包含负圈。
没有负圈当且仅当Opt(i,v)=Opt(i-1,v) 对于所有的v而言。

6.1 带解答的练习
6.1.1 练习1

类似于RNA结构预测:
ej表示比j小但与j相距大于5英里的点i
Opt(j)=max(rj+Opt(Opt(e(j)),Opt(j-1)
所以我们可以根据递推关系得到算法。
#include<iostream>
int Position[n];
int find(){
init(Position);//初始化
init(P);//初始化,令p[j]为距离他小与五英里的点,最近的
m[0]=0;
for(int i=1;i<=n;i++){
M[i]=max(M[i-1],M[P[i]]+rj);
}
return M[n];
}
O(n)
补充,我们也可以将这个问题看做是带权区间调度,我们对于xi考虑(xi-5,xi),权值为r,将其带入到带权区间里也可以得到对应的解。
6.1.2 练习2

我们可考虑该问题类似于分段的最小二乘问题。
类似的考虑最后一段。
Opt=minc(t,j)+Opt(t-1)
Opt(0)=0
ct,j 表示与原串t-j最优的序列比对。
#include<iostream>
int Position[n];
int find(){
for(int t=1;t<=m;t++) {
for(int j=t;j<=m;j++){
计算对应的最优匹配
}
}
M[0]=0;
for(int i=1;i<=n;i++){
int min=0;
int minx=0;
for(int j=1;j<=i;j++){
int x=对应的最优匹配;
}
M[i]=min(min+M[j-1]);
}
return M[n];
}
可知时间为
Om^2
6.2 课后练习
6.2.1 练习1
 a)考虑 2-3-2 此时根据a中的贪婪算法得不到最优解。
a)考虑 2-3-2 此时根据a中的贪婪算法得不到最优解。
b)考虑 3-1-2-3 此时也得不到最优解。
c)时间为O(n)
递推:Opt(i)=max(Opt(i-1),Opt(i-2)+wi);
可知有上述递推得到的算法的时间为On,对于最优解的获取可以反向追M数组。
#include<iostream>
int P[n+1];
void Opt(int n){
M[0]=0;
M[1]=P[1];
for(int i=2;i<=n;i++){
M[i]=max(M[i-2]+P[i],M[i-1]);
}
}
void FindOpt(int n){
if(M[n-2]+P[n]>M[n-1]){
print n;
findOpt(n-2);
}
else{
findOpt(n-1);
}
}
6.2.2 练习2


a):
例子如下:

b):考虑递推式:
Opt(i)=max(Opt(i-1)+li,Opt(i-2)+hi);
Opt(1)=max(l1,h1)
如果要得到最优的解,那么可以进行M数组的反向追踪。
算法的具体时间为O(n)
#include<iostream>
int H[n+1];
int L[n+1];
void Opt(int n){
M[0]=0;
M[1]=P[1];
for(int i=2;i<=n;i++){
M[i]=max(M[i-2]+H[i],M[i-1]+L[i]);
}
}
void FindOpt(int n){
if(M[n-2]+H[n]>M[n-1]+L[n]){
print hn;
findOpt(n-2);
}
else{
print Ln;
findOpt(n-1);
}
}
6.2.3 练习3

a)
考虑例子 v1…v5 其中有边 v1,v2 v1,v3 v2,v5 v3,v4 v4,v5
此时上述算法返回的解不是最优解。
b)
考虑递推式
Opt(n)=max(Opt(n-1)+1,Opt(k)+1);
其中k<n,且右边 (k,n)的节点
6.2.4 练习4


a)
我们考虑n1,n2,n3 1,4,1 以及 s1,s2,s3 =20,1,20
此时会返回一个非最优解。
b)
我们考虑N1 N2 N3 N4 1 100, 1 100,
S1 S2 S4 S4 100,1,100,1
我们呢可知移动的移动的花费远小于n1或者s1的话费。
c)
我们考虑递推关系:
由于此时这一步与上一步有关,所以我们考虑OPTs为这次采用s
OPtn为这次采用n的花费,而其中每种情况有分成两种。
Optn(i)=min(Opts(i-1)+M+ni,Optn(i-1)+ni)
Opts(i)=min(Optn(i-1)+M+si,Opts(n-1)+si)
6.2.5 练习5


我们可以考虑一下的递归:
Opt(n)=max(opt(i-1)+qualit(i,n))
optn表示n个字符的最优分割方式。
如何quality为o1时,此时可知算法的时间复杂度为On2
6.2.6 练习6


考虑一下递推:
Opt(n)=min(Opt(n-1)+L-cn,Opt(j-1)+L-ci…cn);
我们又该递推可以知道算法的时间为On^2;(其中动态规划部分为On)
6.2.7 练习7*

我们在这里回顾第五章时的做法,我们通过递归将n天划分为两部分。其中可知最优解在s1,s2中或者一个在s1,一个在s2,我们的合并操作为On,所以时间复杂度为Onlogn
在这里我们考虑动态规划:
我们考虑OPT(n)表示第n天卖出的收益
那么可以推出:(第n天卖出,或者之前卖出)
OPT(n)=max(0,Opt(n-1)+p[n]-p[n-1]);
6.2.8 练习8(*)

 a)我们考虑这样一个序列:
a)我们考虑这样一个序列:
即将给定的例子中的x4改为2,
此时给出的算法将会在第二秒和第4秒激活EMp;
此时会摧毁3个机器人
而当在第三秒和第四秒时,会摧毁5个机器人,所以不是最优的。
b)
!考虑的是最后一次使用武器充能了多少秒。得到的递推如下。
OPT(j)=max(opt(i)+min(xi,f(j-i))
Opt(0)=0;
6.2.9 练习9
 a)
a)
考虑s1=10,s2=1=s3=s4… xi=11
所以我们会将系统隔一天重启一次。
b)
1)Opt(n)=max(opt(i-1)+i-n这些天处理的数据)
i>=0<=n;
i表示第几天重启。
此递推需要O(n^3)
2)
我们考虑引入新的变量j,令opt(i,j)表示从i-n天的最优解,其中j标志在多少天前重启过。
假设第i天重启:
Opt(i,j)=opt(i+1,1)
不重启:
Opt(i,j)=Opt(i+1,j+1)+min(sj,xi);
由于我们这里考虑的是从i-n天的时间,所以
此时算法迭代中的i为从n-1倒退到1
同时设置初值Opt(n,j)=min{xn,sj) 即最后一天的情况
这种算法即是二层循环,每次为o1
所以得到的算法时间优化为On^2
6.2.10 练习10


 a)
a)
考虑一下例子
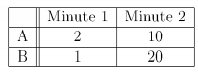
上述算法选择:a,b 他得到的10
而最优为20
补充:
b)类似与之前的n,s办公问题。
考虑如下递推公式:
Opta(n)=max(opta(n-1)+an,optb(n-1)+0);
optb(n)=max(optb(n-1)+bn,opta(n-1)+0);
或者考虑加上变量:
改为如下递推公式
Opta(n)=max(opta(n-1)+an,optb(n-2)+an);
补充:我们考虑第三种:令opt(i) 为 1-i的最优解。
我们初始化Opt(-1)=opt(1)=0
考虑上一次搬移为第k分钟,那么就有opt(i)=max(opt(k-2)+max{aik,bik}
其中k属于(1,i)之间,
6.2.11 练习11
 考虑递推如下:
考虑递推如下:
Opt(n)=min(opt(n-4)+c,opt(n-1)+snr);
n>=4
n<=4
optn=opt(n-1)+snr;
6.2.12 练习12
 考虑递归
考虑递归
OPT(n)=min(Opt(k-1)+sk+n-1个的代价));
k属于(1,n-1)
k表示在n之前的一个放置副本的位置。
6.2.13 练习13
 我们考虑之前的负圈的寻找。
我们考虑之前的负圈的寻找。
我们构造图G,使得别条边(i,j)的权值为logrij 。通过log函数将乘法转换为加法,此时问题就变成了确定在圈C上是否有对应的负圈存在。(存在Opt(i,v)!=Opt(i-1,v))
6.2.14 练习14(?*)
 a)
a)
我们考虑构造图H,他的节点与Gi的节点相同,边由G1,G2.。。Gb中的边构造而成。对于这个图我们可以采用dijstria算法或者BFS来完成。
b)
6.2.15 练习15


a)
给出例子如下:
3,2,-3,-2,-1,0
上述算法给出的结果为2,5,6,而实际的最优解为3456
b)
Opt(n)=1+maxOpt(i)
其中i满足一下条件:
dn-di<=n-i