一文读懂梯度下降法

1. 前言

\qquad 机器学习中的大部分问题都是优化问题，而绝大部分优化问题都可以使用梯度下降法处理，那么搞懂什么是梯度，什么是梯度下降法就非常重要！这是基础中的基础，也是必须掌握的概念！
\qquad 提到梯度，就必须从导数（derivative）、偏导数（partial derivative）和方向导数（directional derivative）讲起，弄清楚这些概念，才能够正确理解为什么在优化问题中使用梯度下降法来优化目标函数，并熟练掌握梯度下降法（Gradient Descent）。

2. 导数（derivative）

\qquad 仅拥有一个自变量的函数称为一元函数，简记为 $y=f(x)$。设函数 $y=f(x)$ 在点 $x_0$ 的某个邻域内有定义，当自变量 $x$ 在 $x_0$ 处有增量 $\Delta x$，$x_0+\Delta x$也在该邻域时，对应的函数取得增量 $\Delta y=f(x_0+\Delta x)-f(x_0)$。如果 $\Delta y$ 与 $\Delta x$ 之比，当 $\Delta x\to 0$ 时，极限存在，则称函数 $f(x)$ 在 $x_0$ 处可导（仅在 $x_0$ 这一点处，并不保证在所有点处），并称这个极限为函数 $y=f(x)$ 在点 $x_0$ 处的导数，记为 $f^{\prime }(x_0)$，即：
$$f^{\prime }(x_0)=\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$$

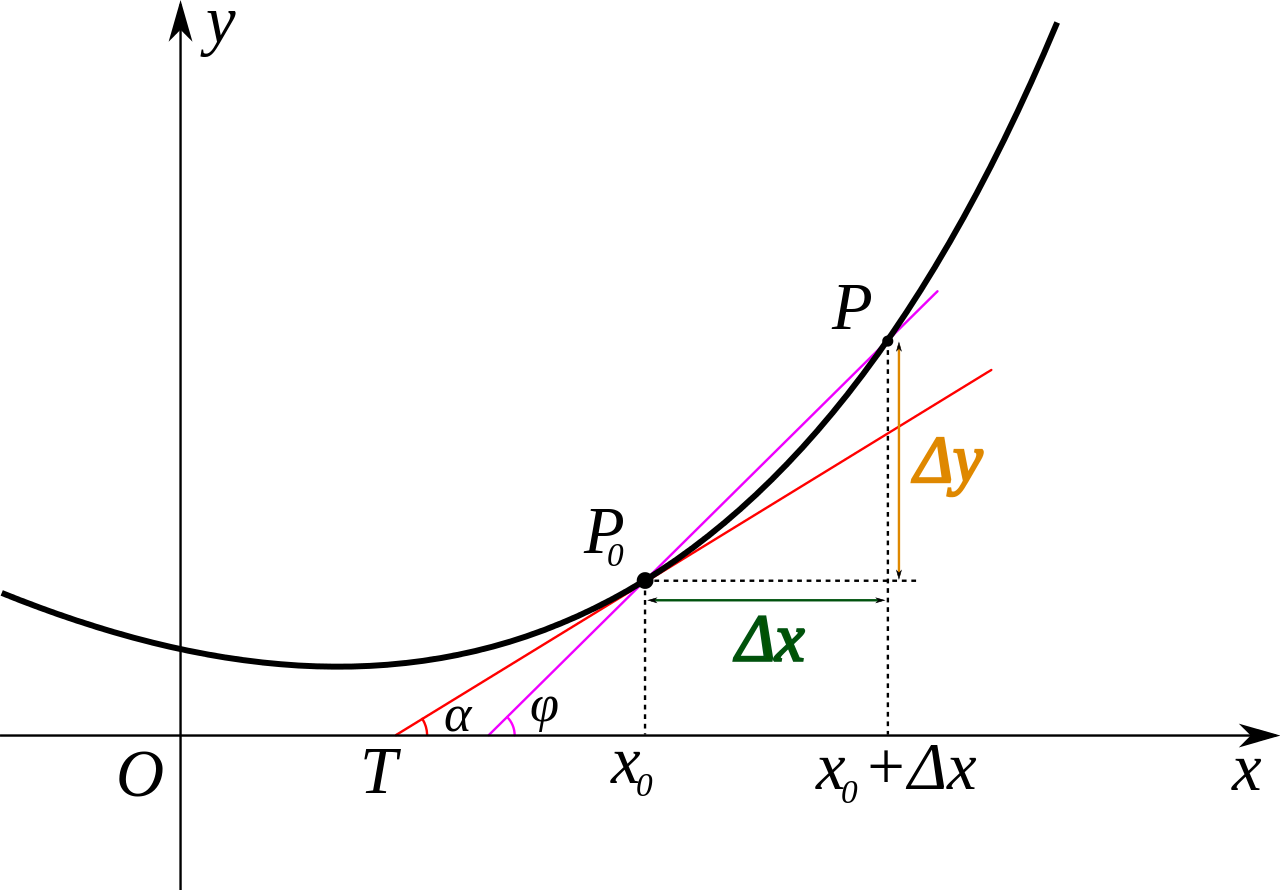
\qquad 由上图可见，导数反映的是函数 $y=f(x)$ 在某一点 $x_0$ 处沿 $x$ 轴正方向的变化率/变化趋势。直观地看，也就是在 $x$ 轴上某一点 $x_0$ 处，如果 $f’(x)>0$，说明 $f(x)$ 的函数值在 $x_0$ 点沿 $x$ 轴正方向是趋于增加的；如果 $f’(x)<0$，说明 $f(x)$ 的函数值在 $x_0$ 点沿 $x$ 轴正方向是趋于减少的。

3. 偏导数（partial derivative）

\qquad 偏导数是多元函数 $y=f(x_0,x_1,\dots ,x_n)$ “退化”成一元函数时的导数，这里“退化”的意思是固定其他变量的值，只保留一个变量，依次保留每个变量，则 $N$ 元函数有 $N$ 个偏导数。偏导数的公式如下：
$$\frac{\partial }{\partial x_j}f(x_0,\cdots ,x_n)=\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{f(x_0,\cdots ,x_j+\Delta x,\cdots ,x_n)-f(x_0,\cdots ,x_j,\cdots ,x_n)}{\Delta x}$$
\qquad 可以看到，导数与偏导数本质是一致的，都是当自变量的变化量趋于 $0$ 时，函数值的变化量与自变量变化量比值的极限。直观地说，偏导数也就是函数在某一点上沿坐标轴正方向的的变化率。

• 导数与偏导数的区别在于：
  • 定义上的区别：导数指的是一元函数中，函数 $y=f(x)$ 在某一点 $x_0$ 处沿 $x$ 轴正方向的变化率；偏导数指的是多元函数中，函数 $y=f(x_0,x_1,\dots ,x_n)$ 在某一点 $x_0$ 处沿某一坐标轴 $(x_0,x_1,\dots ,x_n)$ 正方向的变化率。
  • 几何意义上的区别：导数的几何意义是函数 $y=f(x)$ 曲线在 $x_0$ 点上的切线斜率；偏导数的几何意义是 $y=f(x,y)$ 曲面上 $x_0$ 点在 $x$ 方向或 $y_0$ 点在 $y$ 方向空间曲线的斜率。

4. 方向导数（directional derivative）

\qquad 导数和偏导数均是沿坐标轴正方向讨论函数的变化率，那么当我们讨论函数 $y=f(x_0,x_1,\dots ,x_n)$ 沿任意方向的变化率时，也就引出了方向导数的定义，即：某一点在某一特定方向上的导数值。我们不仅要知道函数在坐标轴正方向上的变化率（即偏导数），而且还要设法求得函数在其他特定方向上的变化率，而方向导数就是函数在其他特定方向上的变化率。方向导数的公式如下：
$$\begin{gathered} \frac{\partial }{\partial x_j}f(x_0,\cdots ,x_n)=\underset{\rho \to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\rho \to 0}{\lim }\frac{f(x_0+\Delta x_0,\cdots ,x_j+\Delta x,\cdots ,x_n+\Delta x_n)-f(x_0,\cdots ,x_j,\cdots x_n)}{\rho } \\ \rho =\sqrt{(\Delta x_0{)}^2+\cdots +(\Delta x_j{)}^2+\cdots +(\Delta x_n{)}^2} \end{gathered}$$
\qquad 下面以二元函数 $z=f(x,y)$ 为例讲解一下方向导数。假设点 $(x_0,y_0)$ 在某一方向的单位向量为 $e_l=(cos\alpha ,sin\alpha )$，$\alpha$ 为此单位向量与 $x$ 轴的正向夹角，显然根据 $\alpha$ 的不同，此向量可以表示任意方向的单位向量。当点 $(x_0,y_0)$ 沿着该方向产生一个增量 $t$ 到达点 $(x_0+tcos\alpha ,y_0+tsin\alpha )$ 时，函数 $z$ 也会产生一个增量 $\Delta z=f(x_0+tcos\alpha ,y_0+tsin\alpha )-f(x_0,y_0)$。此时函数 $z$ 沿此方向的变化率为：
$\underset{t^{+}\to 0}{\lim }\frac{f(x_0+tcos\alpha ,y_0+tsin\alpha )-f(x_0,y_0)}{t}$
$=\underset{t^{+}\to 0}{\lim }[\frac{f(x_0+tcos\alpha ,y_0+tsin\alpha )-f(x_0,y_0+tsin\alpha )}{t}+\frac{f(x_0,y_0+tsin\alpha )-f(x_0,y_0)}{t}]$
$=\underset{t^{+}\to 0}{\lim }[\frac{f_x({\xi }_x,y_0+tsin\alpha )tcos\alpha }{t}+\frac{f_y(x_0,{\xi }_y)tsin\alpha }{t}]({\xi }_x\in (x_0,x_0+tcos\alpha ),{\xi }_y\in (y_0,y_0+tsin\alpha ))$
$(此处应用了拉格朗日中值定理：f(b)-f(a)=f^{\prime }(\xi )(b-a),\xi \in (a,b))$
$=\underset{t^{+}\to 0}{\lim }{f}_x({\xi }_x,y_0+tsin\alpha )\cdot \underset{t^{+}\to 0}{\lim }\frac{tcos\alpha }{t}+\underset{t^{+}\to 0}{\lim }{f}_y(x_0,{\xi }_y)\cdot \underset{t^{+}\to 0}{\lim }\frac{tcos\alpha }{t}$
$=f_x(x_0,y_0)\cdot cos\alpha +f_y(x_0,y_0)\cdot sin\alpha (其中，f_x(x_0,y_0)和f_y(x_0,y_0)分别为函数在点(x_0,y_0)的偏导数)$

5. 向量（vector）

\qquad 向量的定义是有方向（direction）有大小（magnitude）的量。从前面的定义可以这样看出，偏导数和方向导数表达的是函数在某一点沿某一方向的变化率，也是具有方向和大小的。因此从这个角度来理解，我们也可以把偏导数和方向导数看作是一个向量，向量的方向就是变化率的方向，向量的模，就是变化率的大小。

6. 梯度（gradient）

\qquad 在了解了多元函数的方向导数之后，一个很自然的问题是：既然函数在点 $(x_0,y_0)$ 处沿着任意的 $\alpha$ 方向都有一个变化率，那么沿着哪个 $\alpha$ 方向函数的变化率最大呢？
\qquad 根据 $\underset{t^{+}\to 0}{\lim }\frac{f(x_0+tcos\alpha ,y_0+tsin\alpha )-f(x_0,y_0)}{t}=f_x(x_0,y_0)cos\alpha +f_y(x_0,y_0)sin\alpha$ 可知，只需求得使公式达到最大值时的 $\alpha$ 便可解决上述问题。上式可以看成两个向量的内积，令 $\vec{A}=(f_x(x_0,y_0),f_y(x_0,y_0))$，$\overrightarrow{e_l}=(cos\alpha ,sin\alpha )$ 为单位向量，则 $f_x(x_0,y_0)cos\alpha +f_y(x_0,y_0)sin\alpha ={\vec{A}}^T\cdot \overrightarrow{e_l}=|\vec{A}|\cdot |\overrightarrow{e_l}|cos\theta =|\vec{A}|cos\theta$，其中，$\theta$ 为 $\vec{A}$ 和 $\overrightarrow{e_l}$ 的夹角。
\qquad 当给定一个点 $(x_0,y_0)$ 时，可以获得 $\vec{A}=(f_x(x_0,y_0),f_y(x_0,y_0))$，则 $|\vec{A}|$ 的值为固定值，$\underset{t^{+}\to 0}{\lim }\frac{f(x_0+tcos\alpha ,y_0+tsin\alpha )-f(x_0,y_0)}{t}$ 的值仅由 $cos\theta$ 决定，因此可得出如下结论：当 $\theta =0$ 时，即 $\overrightarrow{e_l}$ 和 $\vec{A}$ 方向相同时，函数变化率最大，且在点 $(x_0,y_0)$ 处呈上升趋势；当 $\theta =\pi$ 时，即 $\overrightarrow{e_l}$ 和 $\vec{A}$ 方向相反时，函数变化率最大，且在点 $(x_0,y_0)$ 处呈下降趋势。公式为：
$$gradf(x_0,x_1,\cdots ,x_n)=(\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial x_1},\cdots ,\frac{\partial f}{\partial x_n})$$
\qquad 由此，可以引出梯度的定义：梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。
\qquad 梯度的几何意义：梯度的方向就是多元函数在某一点处增长最快的方向，梯度的模为方向导数的最大值，上式中与 $\overrightarrow{e_l}$ 方向相同的向量 $\vec{A}$ 即是梯度。
\qquad 梯度的重要性质：等高线上点 $p$ 的法向量与该点的梯度方向相同，梯度的方向与等高线切线方向垂直。

7. 梯度下降法（gradient descent）

\qquad 在机器学习算法中，在最小化损失函数时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数，和模型参数值。在变量空间中的某一点，函数沿梯度方向具有最大的变化率，那么在优化目标函数的时候，需要沿着梯度的反方向去减小损失函数值，以此达到我们的优化目标。

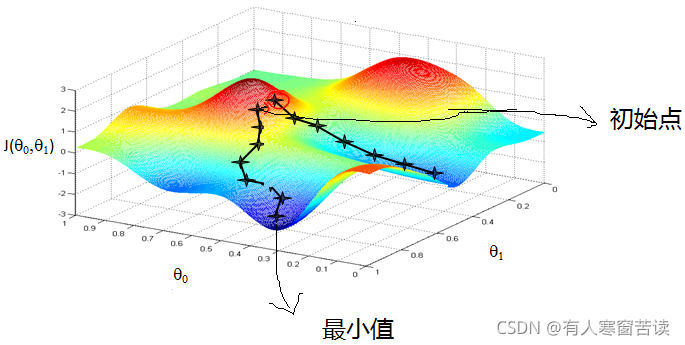
\qquad 梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

7.1 梯度下降的相关概念

1. 学习率(learning rate)：学习率决定了在梯度下降迭代的过程中，每一步沿梯度负方向前进的长度。
2. 特征(feature)：指的是样本中输入部分，比如 $2$ 个单特征的样本$(x^{(0)},y^{(0)}),(x^{(1)},y^{(1)})$，则第一个样本特征为 $x^{(0)}$，第一个样本输出为 $y^{(0)}$。
3. 假设函数(hypothesis function)：在监督学习中，为了拟合输入样本，而使用的假设函数，记为$h_{\theta }(x)$。比如对于单个特征的 $m$ 个样本 $(x^{(i)},y^{(i)})(i=1,2,...m)$，可以采用拟合函数如下： $h_{\theta }(x)={\theta }_0+{\theta }_{1}x$。
4. 损失函数(loss function)：为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。在线性回归中，损失函数通常为样本输出和假设函数的差取平方。比如对于 $m$ 个样本 $(x_i,y_i)(i=1,2,...m)$，采用线性回归，损失函数为：$J({\theta }_1,{\theta }_2)=\sum _{i=1}^m(h_{\theta }(x_i)-y_i{)}^2$，其中 $x_i$ 表示第 $i$ 个样本特征，$y_i$ 表示第 $i$ 个样本对应的输出，$h_{\theta }(x_i)$为假设函数。

7.2 梯度下降的详细算法

\qquad 梯度下降法的算法可以有 $代数法$ 和 $矩阵法$（也称向量法）两种表示。

7.2.1 代数法

1. 先决条件： 确认优化模型的假设函数和损失函数。
   示例：
   \qquad 对于线性回归，假设函数可表示为 $h_{\theta }(x_1,x_2,\cdots ,x_n)={\theta }_0+{\theta }_1{x}_1+\cdots +{\theta }_n{x}_n$，其中 ${\theta }_i(i=0,1,2...n)$ 为模型参数，$x_i(i=0,1,2...n)$ 为每个样本的 $n$ 个特征值。这个表示可以简化，我们增加一个特征 $x_0=1$，这样 $h_{\theta }(x_0,x_1,\cdots ,x_n)=\sum _{i=1}^n{\theta }_i{x}_i$。
   \qquad 线性回归对应于上面假设函数的损失函数为：$J({\theta }_1,{\theta }_2,\cdots ,{\theta }_n)=\frac{1}{2m}\sum _{j=1}^m(h_{\theta }(x_0^{(j)},x_1^{(j)},\cdots ,x_n^{(j)})-y_j{)}^2$。
2. 算法相关参数初始化：主要是初始化 $x_1,x_2,\cdots ,x_n$，算法终止条件 $\epsilon$ 和学习率 $lr$。
3. 算法过程：
   1）确定当前位置的损失函数的梯度，对于 ${\theta }_i$，其梯度表达式如下：$\frac{\partial }{\partial {\theta }_i}J({\theta }_0,{\theta }_1,\cdots ,{\theta }_n)$。
   2）用学习率乘以损失函数的梯度，得到当前位置下降的距离：$lr\cdot \frac{\partial }{\partial {\theta }_i}J({\theta }_0,{\theta }_1,\cdots ,{\theta }_n)$。
   3）确定是否所有的 ${\theta }_i$ 梯度下降的距离都小于 $\epsilon$，如果小于 $\epsilon$ 则算法终止，当前所有的 ${\theta }_i(i=0,1,...n)$ 即为最终结果，否则进入步骤 $4$。
   4）更新所有的 $\theta$，对于 ${\theta }_i$，其更新表达式如下：${\theta }_i={\theta }_i-lr\cdot \frac{\partial }{\partial {\theta }_i}J({\theta }_0,{\theta }_1,\cdots ,{\theta }_n)$。更新完毕后继续转入步骤 $1$。
   示例：
   \qquad 下面用线性回归的例子来具体描述梯度下降。假设我们的样本是$(x_0^{(1)},x_1^{(1)},\cdots ,x_n^{(1)},y_1),(x_0^{(2)},x_1^{(2)},\cdots ,x_n^{(2)},y_2),\cdots ,(x_0^{(m)},x_1^{(m)},\cdots ,x_n^{(m)},y_m)$，则在算法过程步骤 $1$ 中对于 ${\theta }_i$ 的偏导数计算如下：
   $$\frac{\partial }{\partial {\theta }_i}J({\theta }_1,{\theta }_2,\cdots ,{\theta }_n)=\frac{1}{m}\sum _{j=1}^m(h_{\theta }(x_0^{(j)},x_1^{(j)},\cdots ,x_n^{(j)})-y_j)x_i^{(j)}$$
   \qquad 步骤 $2$ 得到当前位置下降的距离：$lr\cdot \frac{\partial }{\partial {\theta }_i}J({\theta }_0,{\theta }_1,\cdots ,{\theta }_n)$
   \qquad 步骤 $4$ 中 ${\theta }_i$ 的更新表达式如下：
   $${\theta }_i={\theta }_i-lr\cdot \frac{1}{m}\sum _{j=1}^m(h_{\theta }(x_0^{(j)},x_1^{(j)},\cdots ,x_n^{(j)})-y_j)x_i^{(j)}$$

7.2.2 矩阵法

1. 先决条件： 确认优化模型的假设函数和损失函数。
   示例：
   \qquad 对于线性回归，假设我们的样本是$(x_0^{(1)},x_1^{(1)},\cdots ,x_n^{(1)},y_1),(x_0^{(2)},x_1^{(2)},\cdots ,x_n^{(2)},y_2),\cdots ,(x_0^{(m)},x_1^{(m)},\cdots ,x_n^{(m)},y_m)$，假设函数 $h_{\theta }(x_1,x_2,\cdots ,x_n)={\theta }_0+{\theta }_1{x}_1+\cdots +{\theta }_n{x}_n$ 的矩阵表达方式为：$h_{\theta }(X)=X\theta$，其中，假设函数 $h_{\theta }(X)$ 为 $m\times 1$ 的向量，$\theta$ 为 $(n+1)\times 1$ 的向量，$X$ 为 $m\times (n+1)$ 维的矩阵。其中，$m$ 代表样本的个数，$n+1$ 代表样本的特征数。
   \qquad 损失函数的表达式为：$J(\theta )=\frac{1}{2}(X\theta -Y{)}^T(X\theta -Y)$，其中 $Y$ 是样本的输出向量，维度为 $m\times 1$。
2. 算法相关参数初始化：主要是初始化 $\theta$ 向量，算法终止条件 $\epsilon$ 和学习率 $lr$。
3. 算法过程：
   1）确定当前位置的损失函数的梯度，对于 $\theta$ 向量，其梯度表达式如下：$\frac{\partial }{\partial \theta }J(\theta )$。
   2）用学习率乘以损失函数的梯度，得到当前位置下降的距离：$lr\cdot \frac{\partial }{\partial \theta }J(\theta )$。
   3）确定 $\theta$ 向量里面的每个值，梯度下降的距离都小于 $\epsilon$，如果小于 $\epsilon$ 则算法终止，当前 $\theta$ 向量即为最终结果。否则进入步骤 $4$。
   4）更新 $\theta$ 向量，其更新表达式如下：$\theta =\theta -lr\cdot \frac{\partial }{\partial \theta }J(\theta )$。更新完毕后继续转入步骤 $1$。
   示例：
   \qquad 下面用线性回归的例子来具体描述梯度下降。在算法过程步骤 $1$ 中对于 $\theta$ 向量的偏导数计算如下：$\frac{\partial }{\partial \theta }J(\theta )=X^T(X\theta -Y)$
   \qquad 步骤 $2$ 得到当前位置下降的距离：$lr\cdot X^T(X\theta -Y)$
   \qquad 步骤 $4$ 中 ${\theta }_i$ 的更新表达式如下：$\theta =\theta -lr\cdot X^T(X\theta -Y)$

7.3 梯度下降的算法调优

1. 算法的学习率选择。学习率太大，会导致迭代过快，甚至有可能错过最优解。学习率太小，迭代速度太慢，很长时间算法都不能结束。
2. 算法参数的初始值选择。初始值不同，获得的最小值也有可能不同，获得的最优解或许只是局部最小值；如果损失函数是凸函数则一定存在全局最优解。由于存在局部最小值的风险，因此需要多次使用不同初始值运行算法，获取损失函数的最小值。
3. 归一化。由于样本的不同特征取值范围不一样，可能导致迭代很慢，因此为了减少特征取值范围的影响，可以对特征数据归一化，也就是对于每个特征 $x$，求出它的期望 $\overline{x}$ 和标准差 $std(x)$，然后将每个特征 $x$ 转化为：$\frac{x-\overline{x}}{std(x)}$，这样特征的新期望为 $0$，新方差为 $1$，迭代速度可以大大加快。

7.4 常用梯度下降法

7.4.1 批量梯度下降法（Batch Gradient Descent）

\qquad 批量梯度下降法，是梯度下降法最常用的形式，具体做法也就是在更新参数时使用所有的样本来进行更新。
$$\begin{gathered} {\theta }_i={\theta }_i-lr\cdot \sum _{j=1}^m\frac{\partial }{\partial {\theta }_i}J({\theta }_0,{\theta }_1,\cdots ,{\theta }_n) \\ 线性回归：{\theta }_i={\theta }_i-lr\cdot \frac{1}{m}\sum _{j=1}^m(h_{\theta }(x_0^{(j)},x_1^{(j)},\cdots ,x_n^{(j)})-y_j)\cdot x_i^{(j)} \end{gathered}$$

7.4.2 随机梯度下降法（Stochastic Gradient Descent）

\qquad 随机梯度下降法，其实和批量梯度下降法原理类似，区别在与求梯度时没有使用所有的 $m$ 个样本的数据，而是仅仅选取一个样本 $j$ 来求梯度。对应的更新公式是：
$$\begin{gathered} {\theta }_i={\theta }_i-lr\cdot \frac{\partial }{\partial {\theta }_i}J({\theta }_0,{\theta }_1,\cdots ,{\theta }_n) \\ 线性回归：{\theta }_i={\theta }_i-lr\cdot (h_{\theta }(x_0^{(j)},x_1^{(j)},\cdots ,x_n^{(j)})-y_j)\cdot x_i^{(j)} \end{gathered}$$
\qquad 随机梯度下降法与批量梯度下降法是两个极端，一个采用所有数据进行梯度下降，一个采用一个样本进行梯度下降。自然各自的优缺点都非常突出。对于 $训练速度$ 来说，随机梯度下降法由于每次仅仅采用一个样本来迭代，训练速度很快，而批量梯度下降法在样本量很大的时候，训练速度不能让人满意；对于 $准确度$ 来说，随机梯度下降法仅采用一个样本决定梯度方向，导致解很有可能不是最优；对于 $收敛速度$ 来说，由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。

7.4.3 小批量梯度下降法（Mini-batch Gradient Descent）

\qquad 大多数用于深度学习的梯度下降算法介于以上两者之间，使用一个以上而又不是全部的训练样本，这种方法会被称为小批量梯度下降法（Mini-batch Gradient Descent）。小批量梯度下降法是批量梯度下降法和随机梯度下降法的折中，也就是对于 $m$ 个样本，我们随机采用 $x$ 个样本来迭代，$1<x<m$。一般可以取 $x=10$，当然根据样本的数据，可以调整这个 $x$ 的值。
$$\begin{gathered} {\theta }_i={\theta }_i-lr\cdot \sum _{j=t}^{t+x-1}\frac{\partial }{\partial {\theta }_i}J({\theta }_0,{\theta }_1,\cdots ,{\theta }_n) \\ 线性回归：{\theta }_i={\theta }_i-lr\cdot \frac{1}{x}\cdot \sum _{j=t}^{t+x-1}(h_{\theta }(x_0^{(j)},x_1^{(j)},\cdots ,x_n^{(j)})-y_j)\cdot x_i^{(j)} \end{gathered}$$