序言
又鸽了很长一段时间，差不多半个多月，很多琐屑轮番来扰很是抽不开身，加上凡事总是要拖到最后的尿性，抽时间写点东西实在是件奢侈的勾当。开学不到一个月以来，除了坚持康复训练终于把10km跑回到45分钟以内，重新点燃了去跑半马的希望，也便是在浑浑噩噩，三点一线式地活着。
事实上这种生活节奏也没有什么不好的，最近发现某人改了签名——该吃吃该喝喝遇事别往心里搁，还把moment限制成近一个月可见，约莫是遭了些许不顺，愿君安好。另一位老朋友闭关一年，终于二战过线，距离上岸一步之遥，邀笔者明天聊聊复试的事情。与老友会面，在平淡中何尝不是快事一件？
人生之不如意十有八九，常想一二。人的悲喜终是不相通的，此刻因他人之喜而喜，幸甚至哉。
回归正题，在今晚S老师的课上，他分享了一道很有趣的问题。如下所示：
其中 P P ( λ ) PP(\lambda) PP(λ)指参数为 λ \lambda λ的泊松过程。
题外话，老实说现在已经没有前四年，更不用说高中那段时间乐于解难题的热情了，大多数时候，十分钟想不出思路的作业题就只能求诸答案，或是前辈的作业，谈不上懒惰，只是到了这个年岁，学习早已不再是生命的一切，要找工作的疲于实习、面试，要读博士的疲于论文、科研，哪还有那么多时间分配在思考很多不久的将来几乎不再可能碰到的问题？正如最近碰到yy时跟笔者说他已经一个星期没上课了（一直在BAT面试实习，实在是脱不开身）。yy说在学校不上课，就跟在上班摸鱼一个道理，本质上这才是赚到了，笔者一时间觉得这句话竟然还是有那么一丝合理的。
好了不扯远了， S S S老师给了我们三分钟时间思考，笔者也是觉得此题很有趣，但是实在是没有能在给定时间内想出来，最后 S S S老师看大家都没有太多头绪，也便是公布了解题思路。
看到这里各位读者也可以稍作思考，这个问题其实看起来非常简单，但是一上手就会发现非常棘手。给个小提示，这个问题是跟在下面这个定理之后的：
其中 N ( t ) N(t) N(t)指在 [ 0 , t ] [0,t] [0,t]时间上泊松过程发生事件的次数， S i S_i Si是第 i i i个事件发生的时刻；
有挑战心的朋友可以想想有没有解题思路哈
也不必勉强，伏行且艰，本是轻松一刻，又何必给自己徒增烦恼，直接往下看吧。
解题思路
这个问题的解题关键就在于，一旦你被给定了这个定理，思维就固化在了一维上。
这个定理其实揭示了泊松过程非常好的一个性质，就是在已知某段时间内事件发生了 n n n次，那么这 n n n次事件发生的确切时刻是相互独立的（进一步地，它们是服从给定区间上的均匀分布）。于是就会很容易固化在考察滚石掉落的坐标 x x x，而忽视了主角的移动。
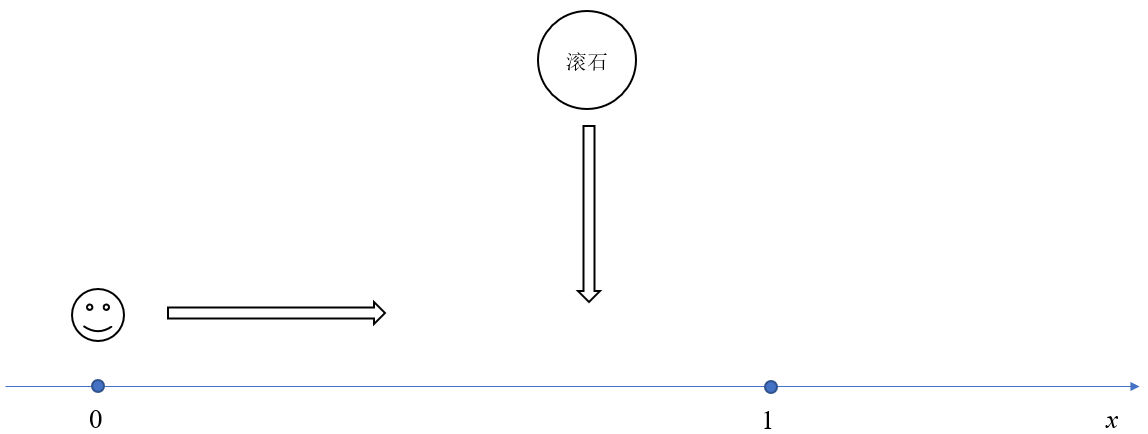事实上如果在上图中扩充一个时间维度，问题就变得豁然开朗：
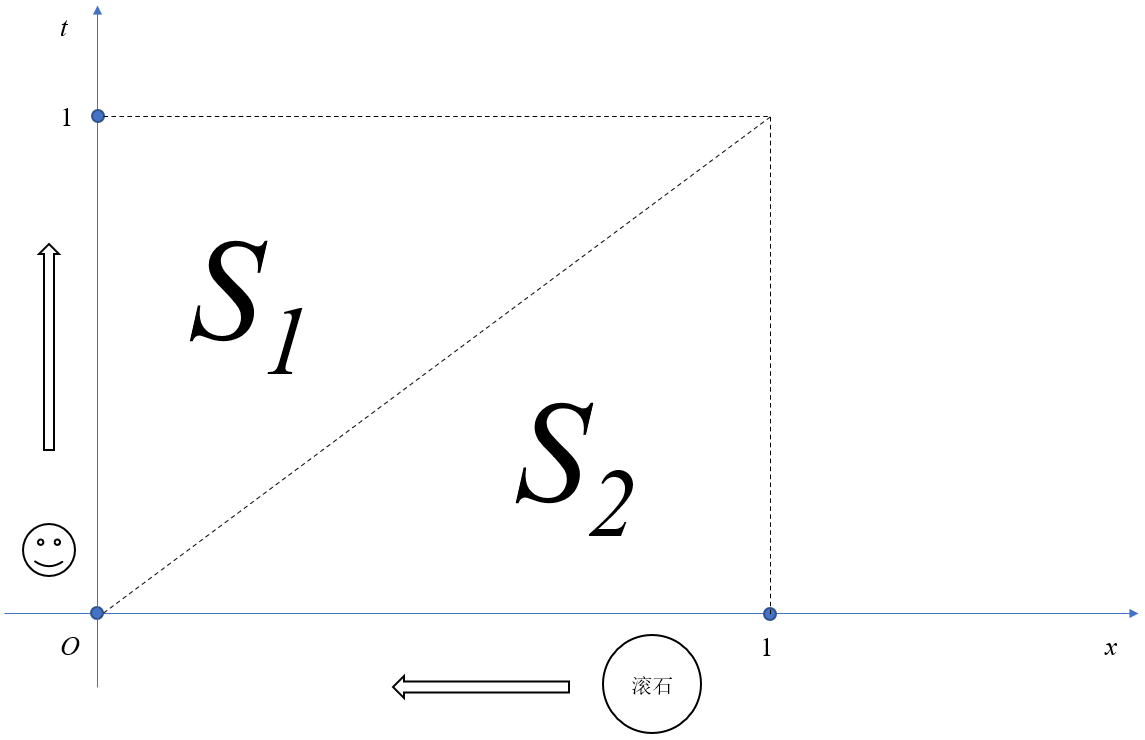显然主角走完区间 [ 0 , 1 ] [0,1] [0,1]需要 1 1 1单位的时间（ 1 1 1分钟），滚石也只会落在 [ 0 , 1 ] [0,1] [0,1]的区间上，那么在什么情况下滚石会砸死主角？显然是当滚石掉落的坐标大于主角已经行走的时间，即滚石掉落的时间，在上图中即是 S 1 S_1 S1区域；
也就是说除非滚石掉落的坐标大于滚石掉落的时刻，主角才会死亡，于是我们需要考察这个事件（即事件发生在 S 1 S_1 S1区域中）的概率有多大？
幸运地是，主角是匀速前行的，因此 t t t轴上是均匀分布的，那么滚石掉落的坐标是否也是均匀分布的呢？
上述定理给出了回答，假设在 [ 0 , 1 ] [0,1] [0,1]的时间内，一共发生了 n n n次落石，它们掉落的坐标是 S 1 , S 2 , . . . , S n S_1,S_2,...,S_n S1,S2,...,Sn，这些坐标恰好就是落石掉落的时刻，根据定理， S 1 , S 2 , . . . , S n S_1,S_2,...,S_n S1,S2,...,Sn等价于是在 [ 0 , 1 ] [0,1] [0,1]区间上的 n n n个独立均匀分布的随机变量，因此这也是均匀的。
于是我们立刻可以得出 n n n个落石砸死主角的概率恰好就是 ( 1 2 ) n \left(\frac{1}{2}\right)^n (21)n，当然一块落石砸死主角的概率就是 1 2 \frac{1}{2} 21，非常直觉的一个结论。
最后我们只需要将 n = 1 , 2 , 3 , . . . n=1,2,3,... n=1,2,3,...的概率累和即可得出主角死亡的概率：
P ( s u r v i v e ) = ∑ n = 0 + ∞ ( 1 2 ) n ⋅ Pr ( N ( 1 ) = n ) = ∑ n = 0 + ∞ ( 1 2 ) n ⋅ λ n n ! e − λ = e − λ 2 [ ∑ n = 1 + ∞ ( λ 2 ) 2 n ! e − λ 2 ] = e − λ 2 \begin{aligned} P(\rm survive)&=\sum_{n=0}^{+\infty}\left(\frac{1}{2}\right)^n\cdot\Pr\left(N(1)=n\right)\\ &=\sum_{n=0}^{+\infty}\left(\frac{1}{2}\right)^n\cdot\frac{\lambda^n}{n!}e^{-\lambda}\\ &=e^{-\frac{\lambda}{2}}\left[\sum_{n=1}^{+\infty}\frac{\left(\frac{\lambda}{2}\right)^2}{n!}e^{-\frac{\lambda}{2}}\right]\\ &=e^{-\frac{\lambda}{2}} \end{aligned} P(survive)=n=0∑+∞(21)n⋅Pr(N(1)=n)=n=0∑+∞(21)n⋅n!λne−λ=e−2λ[n=1∑+∞n!(2λ)2e−2λ]=e−2λ
这个答案并不十分显然，至少作为填空题不容易蒙对。
可以看出随着 λ \lambda λ的增大（即泊松过程到来强度的增强），主角的存活率将呈指数级下降。
后记
近期笔者在看property testing方向的东西，这是个非常小众的领域，但是在计算机图论方面是个很宏大的课题，其实这个跟笔者的方向也不搭，奈何要做汇报，近期可能会发一些阅读笔记，其实个问题还是比较有趣的，可惜看起来很费时间，而且也确实跟NLP能联系的不多。
且行且珍惜。