简明易懂的算法文章-了解AVL树

文章目录

在本教程中，您将学习什么是avl树。此外，您还将找到在C上执行AVL树的示例。
AVL树是一种自平衡二叉搜索树，其中每个节点维护称为平衡因子的额外信息，其值为-1、0或+1。
AVL树以其发明者Georgy Adelson-Velsky和Landis得名。

1. 平衡因子

AVL树中节点的平衡因子是该节点左子树和右子树的高度之差。
平衡因子=（左子树的高度-右子树的高度）或（右子树的高度-左子树的高度）
avl树的自平衡特性由平衡因子来维持。平衡因子的值应始终为-1、0或+1。
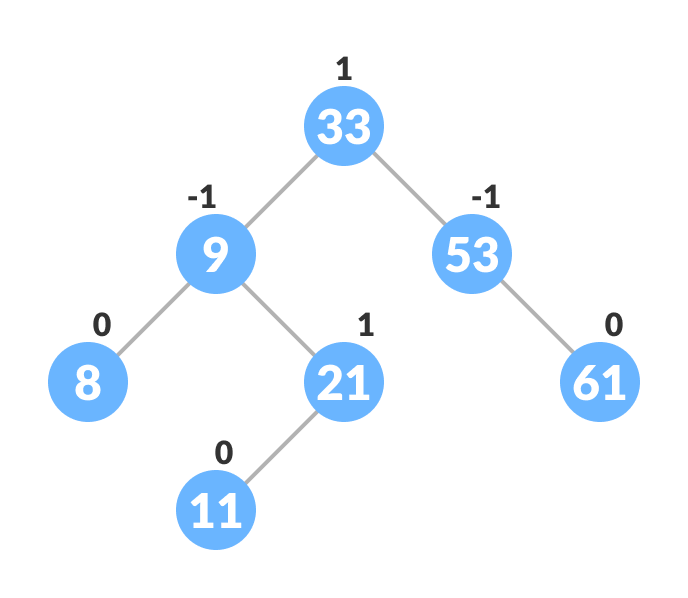
平衡avl树的示例如下：
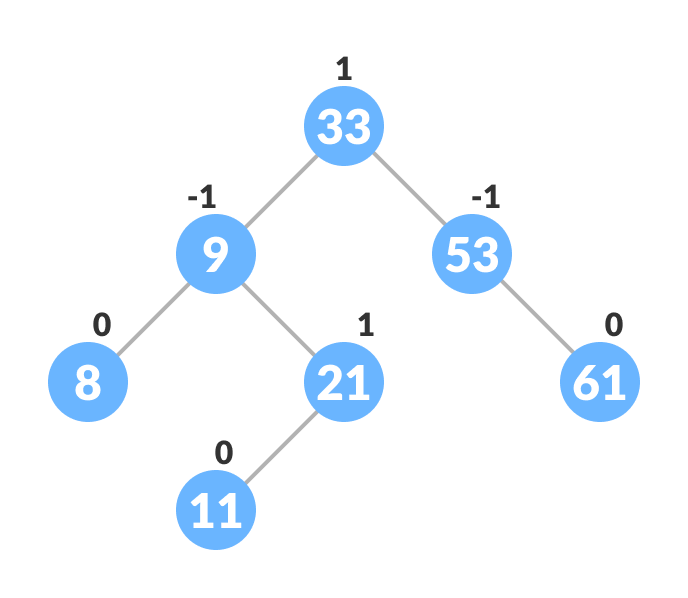
在这里插入图片描述

2. AVL树的操作

可以在AVL树上执行的操作是：

2.1 旋转AVL树中的子树

在旋转操作中，子树节点的位置是互换的。
旋转有两种类型：

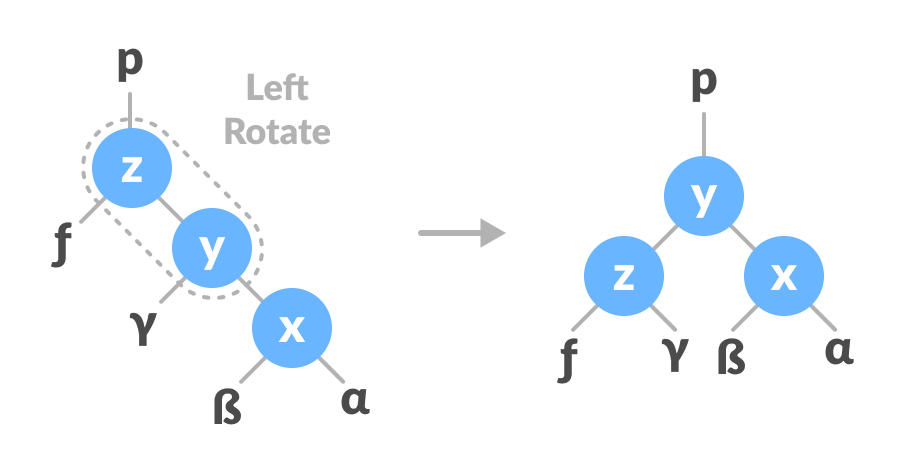
2.1.1 左旋转

在左旋转中，右侧节点的排列转换为左侧节点的排列。

初始树为：
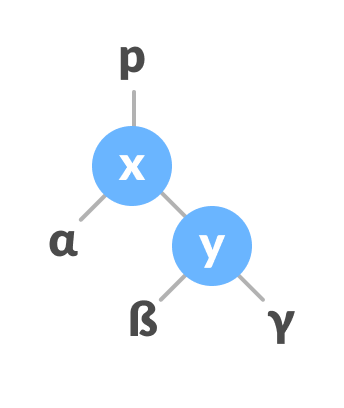
如果y有左子树，则指定x作为y的左子树的父级。
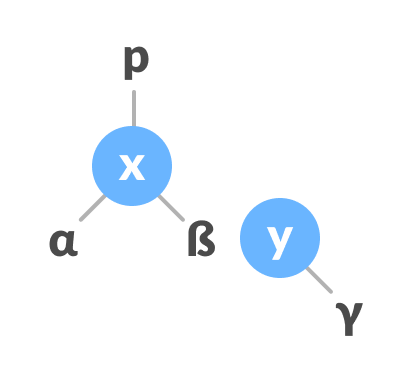
如果x的父级为空，则将y作为树的根。
否则，如果x是p的左子级，则将y作为p的左子级。
否则指定y作为p的右子级。
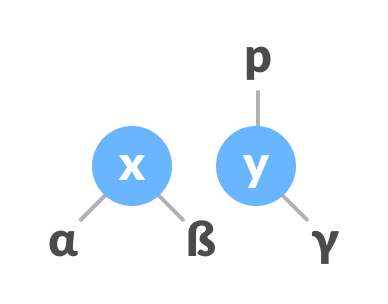
使y成为x的父级。

2.1.2 右旋转

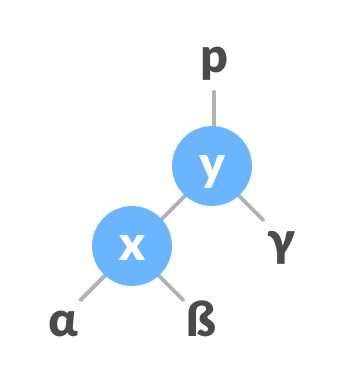
在右旋转中，左侧节点的排列转换为右侧节点的排列。

初始树为：
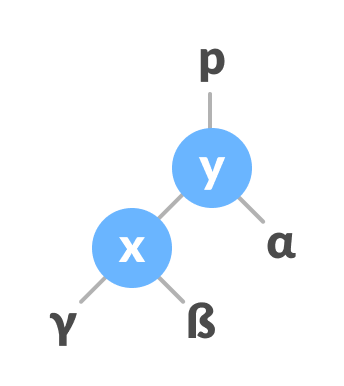
如果x有一个右子树，则指定y作为x的右子树的父树。
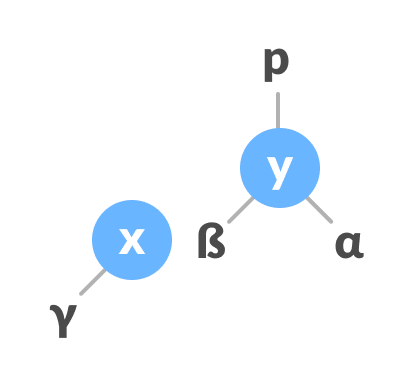
如果y的父级为空，则将x作为树的根。
否则，如果y是其父p的右子级，则使x成为p的右子级。
否则指定x作为p的左子级。
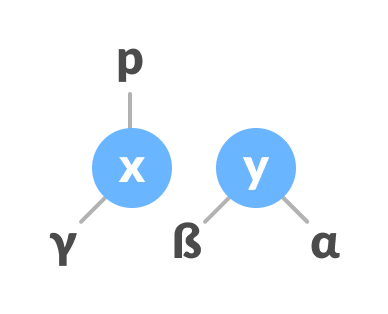
使x成为y的父级。

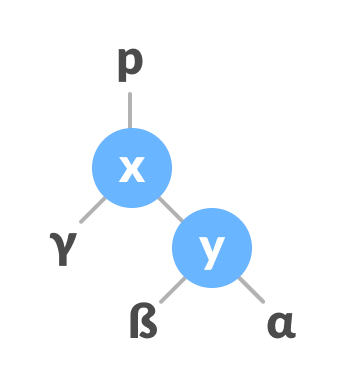
2.1.3 左右和右左旋转

在左右旋转中，排列首先向左移动，然后向右移动。

在X-Y上做左旋转
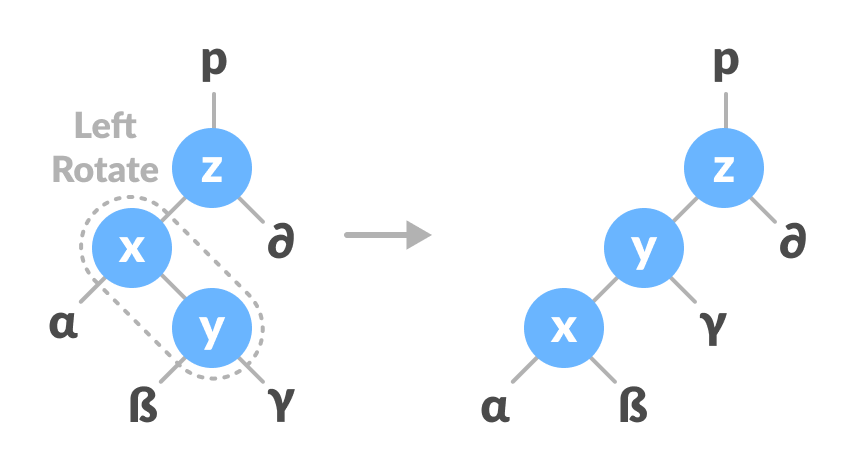
在Y-Z上做右旋转。

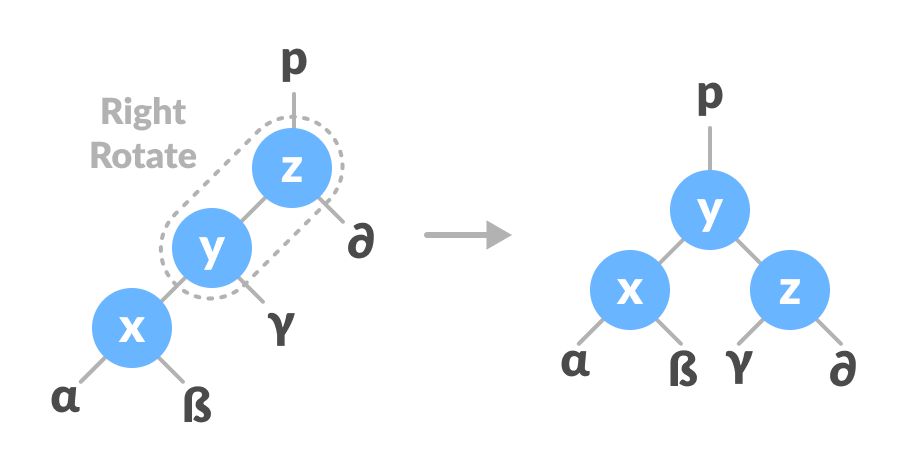
在右左旋转中，排列首先向右移动，然后向左移动。

在X-Y上进行右旋转。
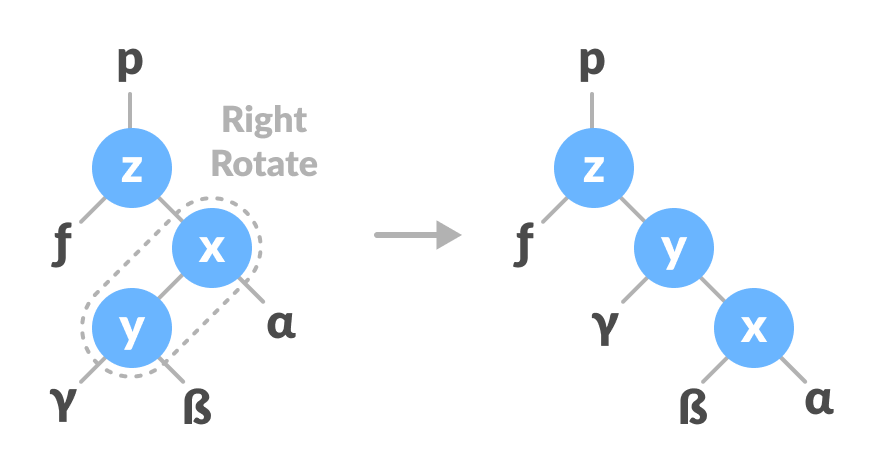
在Z-Y上做左旋转。

2.2 插入新节点的算法

新节点（newNode）始终作为平衡因子为0的叶节点插入。

初始树为：

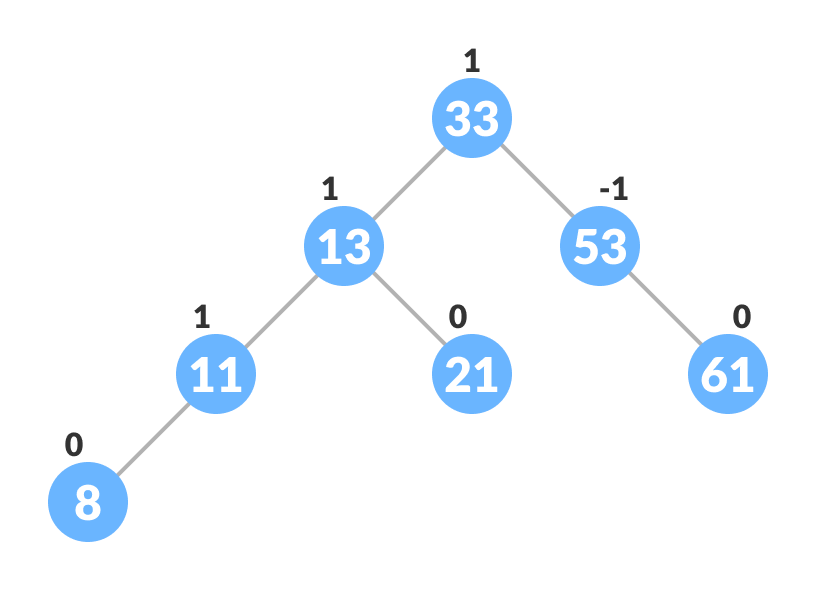
要插入的节点为：
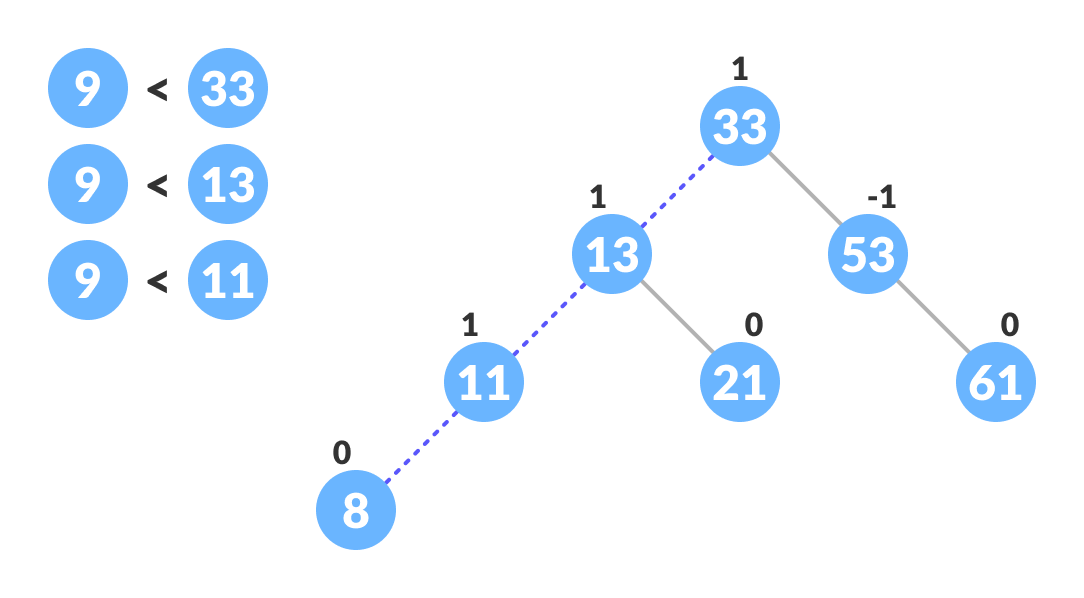
使用以下递归步骤转到相应的叶节点以插入新节点（newNode）。将newKey与当前树的rootKey进行比较。
a. 如果newKey<rootKey，则在当前节点的左子树上调用插入算法，直到到达叶节点为止。
b. 否则，如果newKey>rootKey，则在当前节点的右子树上调用插入算法，直到到达叶节点为止。
c. 否则，返回leafNode。
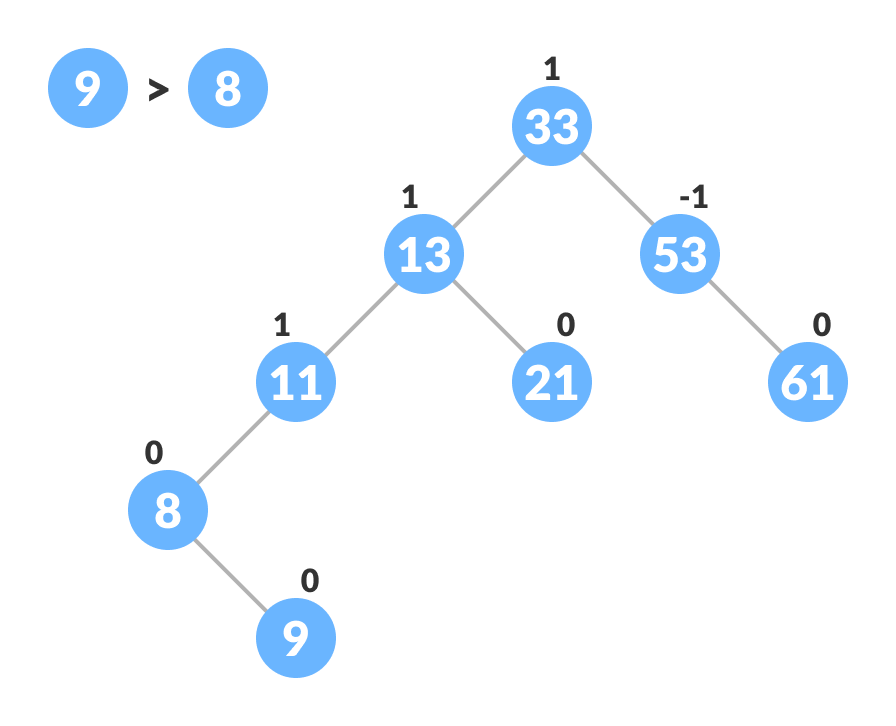
将从上述步骤获得的leafKey与newKey进行比较：
a. 如果newKey<leafKey，则将newNode设为leafNode的左孩子。
b. 否则，将newNode设为leafNode的右孩子。
更新节点的平衡因子。
如果节点不平衡，则重新平衡节点。
a. 如果平衡因子大于1，则表示左子树的高度大于右子树的高度。所以，做一个右旋转或左右旋转
a. 如果newNodeKey<leftChildKey执行右旋转
b. 否则，执行左右旋转

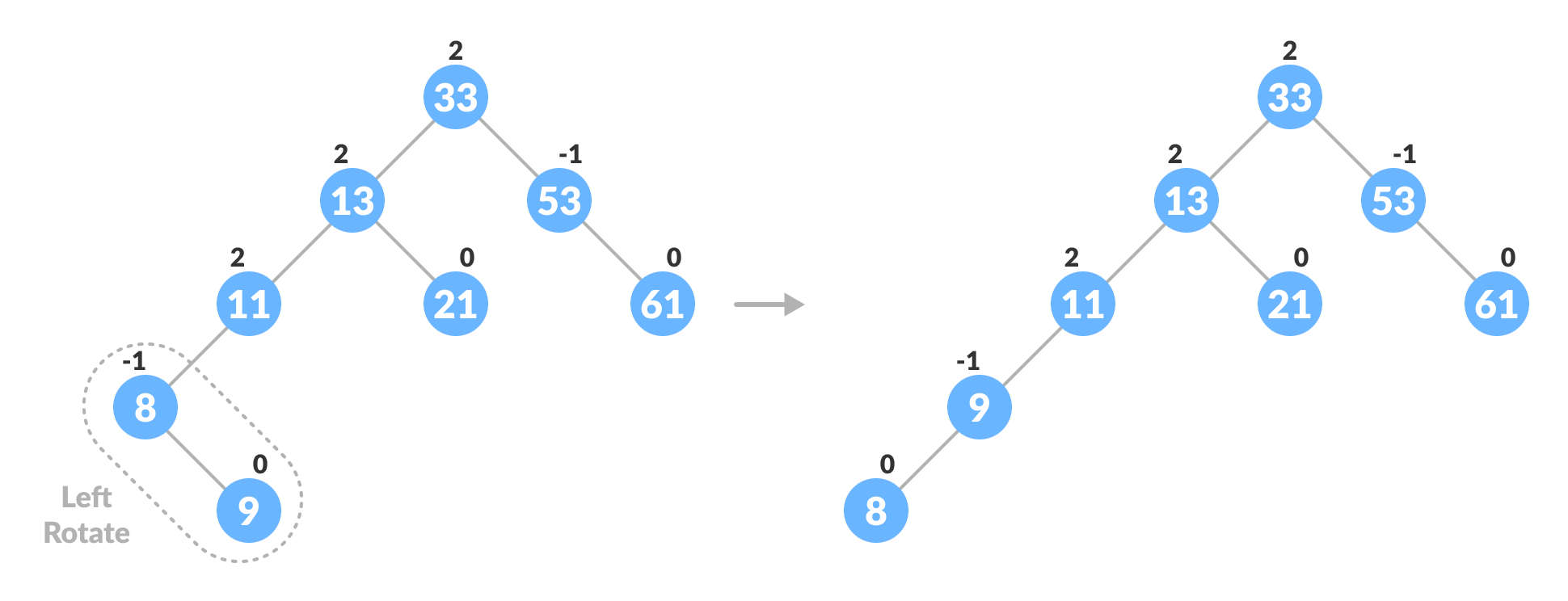
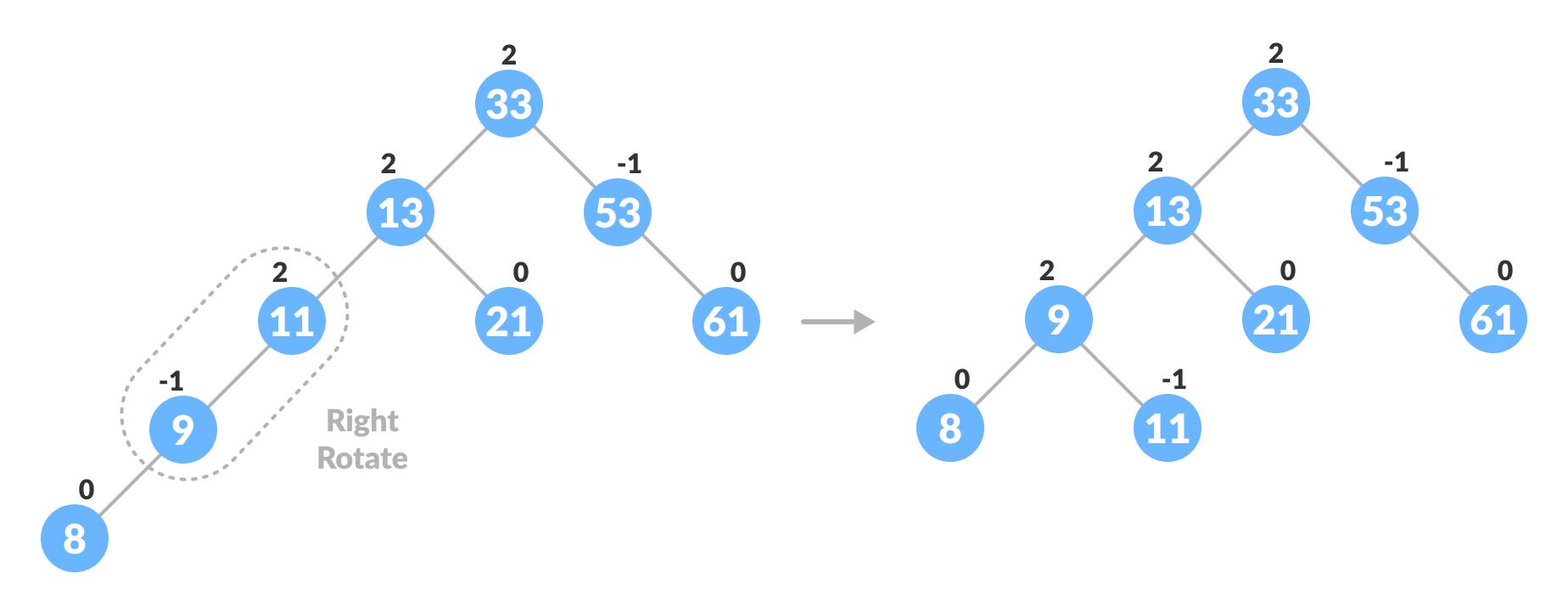
b. 如果平衡因子<-1，则表示右子树的高度大于左子树的高度。所以，做右旋转或左右旋转。
a. 如果newNodeKey>rightChildKey，执行左旋转。
b. 否则，执行右左旋转。
最终树为：

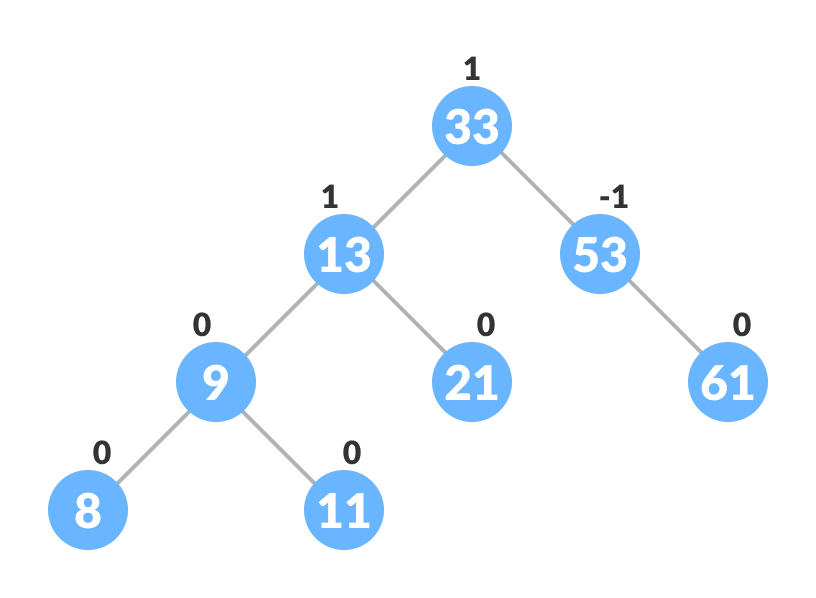
2.3 删除节点的算法

节点始终作为叶节点删除。删除节点后，节点的平衡因子会发生变化。为了重新平衡平衡因子，需要进行适当的旋转。

查找待删除的节点（递归用于在下面使用的代码中查找待删除的节点）。
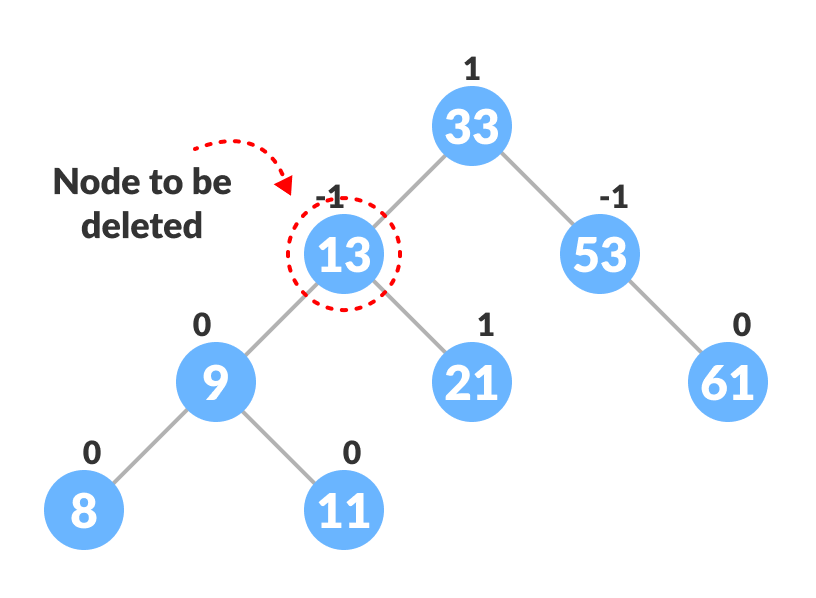
删除节点有以下三种情况：
a. 如果待删除节点是叶节点（即没有任何子节点），则直接删除。
b. 如果待删除节点有一个子级，则用子级的内容替换待删除节点的内容，然后移除子级。
c. 如果待删除节点有两个子节点，则查找待删除节点的顺序继承节点w（即右子树中key值最小的节点）。

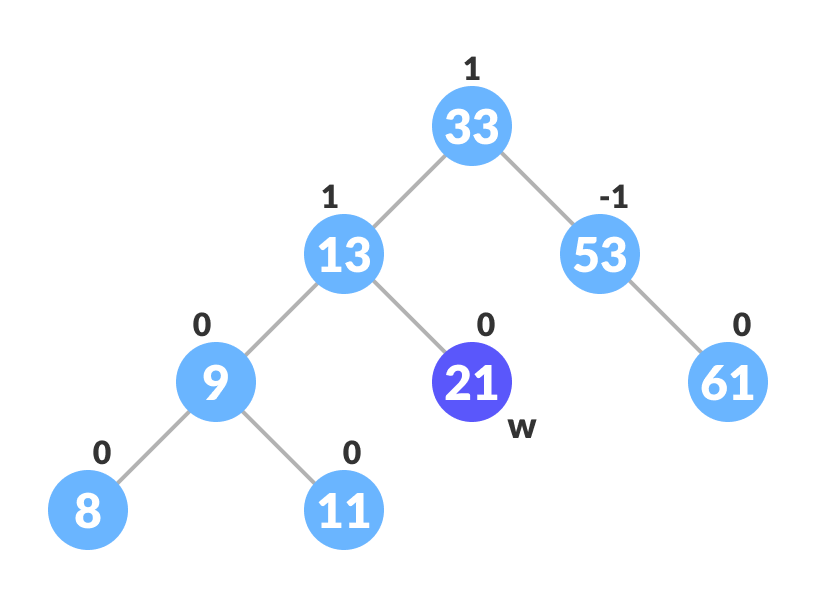
a. 将待删除节点的内容替换为w的内容

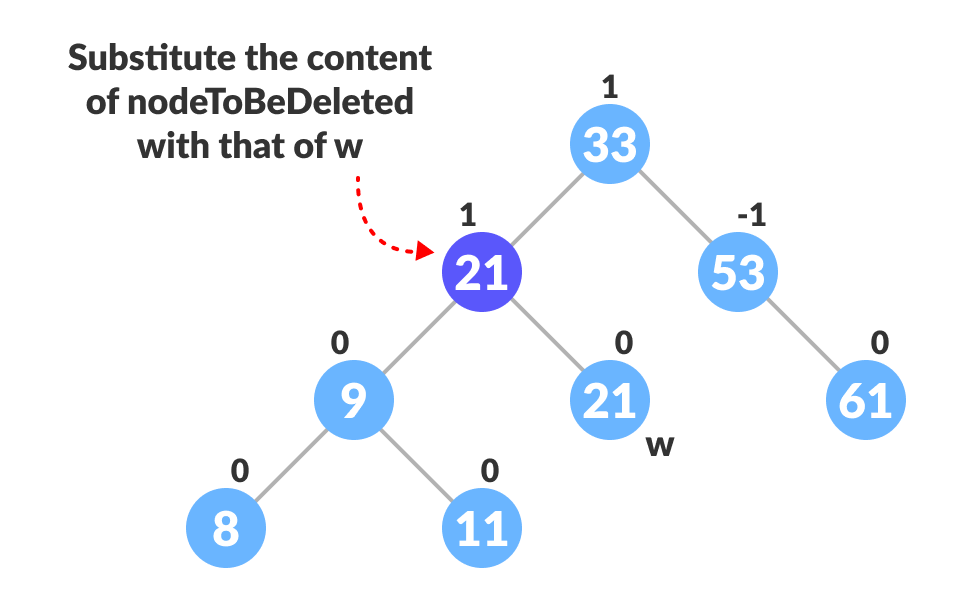
b. 移除叶节点w。
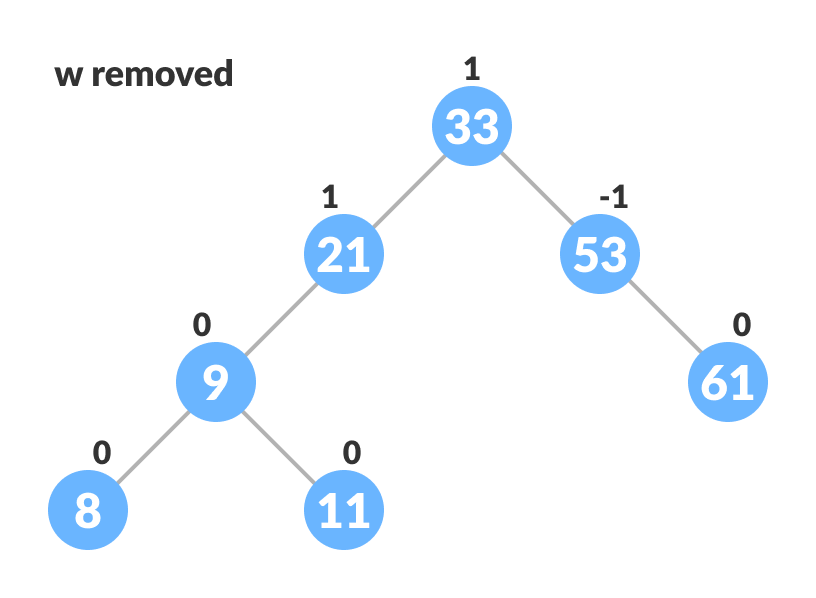
更新节点的平衡因子。
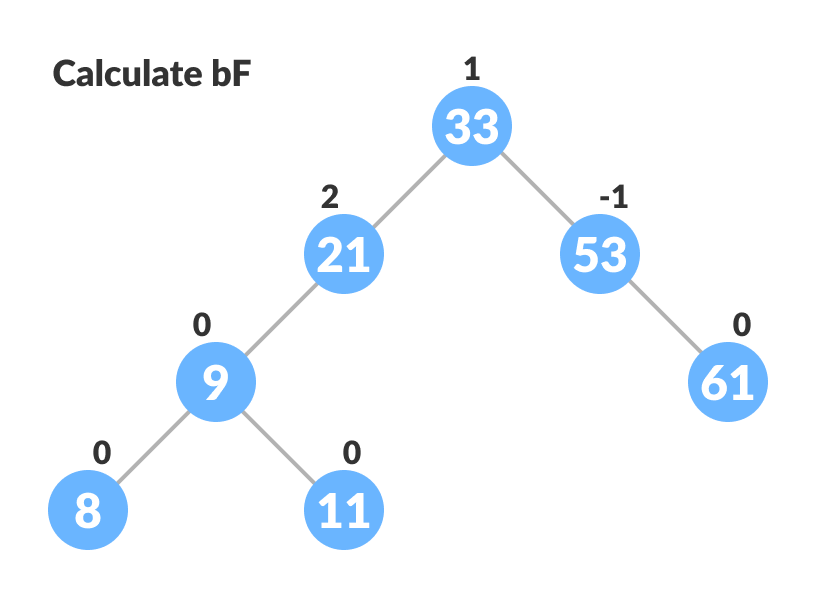
如果任何节点的平衡因子不等于-1、0或1，则重新平衡树。
a. 如果当前节点的平衡因子大于1，
a. 如果左孩子的平衡因子 >= 0，执行右旋转。

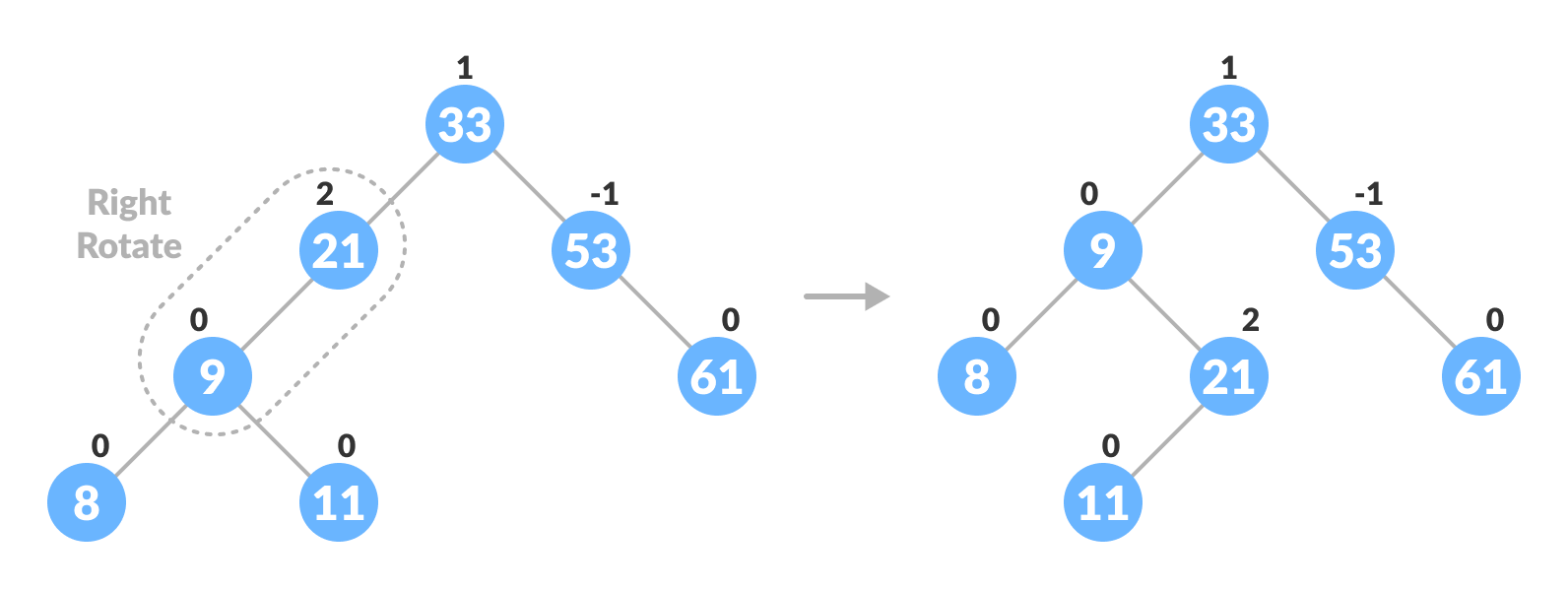
b. 否则执行左右旋转。
b. 如果当前节点的平衡因子小于 -1，
a. 如果右孩子的平衡因子 <= 0，执行左旋转。
b. 否则执行右左旋转。
最终树为：

3. C示例

// AVL tree implementation in C

#include <stdio.h>
#include <stdlib.h>

// Create Node
struct Node {
    
    
  int key;
  struct Node *left;
  struct Node *right;
  int height;
};

int max(int a, int b);

// Calculate height
int height(struct Node *N) {
    
    
  if (N == NULL)
    return 0;
  return N->height;
}

int max(int a, int b) {
    
    
  return (a > b) ? a : b;
}

// Create a node
struct Node *newNode(int key) {
    
    
  struct Node *node = (struct Node *)
    malloc(sizeof(struct Node));
  node->key = key;
  node->left = NULL;
  node->right = NULL;
  node->height = 1;
  return (node);
}

// Right rotate
struct Node *rightRotate(struct Node *y) {
    
    
  struct Node *x = y->left;
  struct Node *T2 = x->right;

  x->right = y;
  y->left = T2;

  y->height = max(height(y->left), height(y->right)) + 1;
  x->height = max(height(x->left), height(x->right)) + 1;

  return x;
}

// Left rotate
struct Node *leftRotate(struct Node *x) {
    
    
  struct Node *y = x->right;
  struct Node *T2 = y->left;

  y->left = x;
  x->right = T2;

  x->height = max(height(x->left), height(x->right)) + 1;
  y->height = max(height(y->left), height(y->right)) + 1;

  return y;
}

// Get the balance factor
int getBalance(struct Node *N) {
    
    
  if (N == NULL)
    return 0;
  return height(N->left) - height(N->right);
}

// Insert node
struct Node *insertNode(struct Node *node, int key) {
    
    
  // Find the correct position to insertNode the node and insertNode it
  if (node == NULL)
    return (newNode(key));

  if (key < node->key)
    node->left = insertNode(node->left, key);
  else if (key > node->key)
    node->right = insertNode(node->right, key);
  else
    return node;

  // Update the balance factor of each node and
  // Balance the tree
  node->height = 1 + max(height(node->left),
               height(node->right));

  int balance = getBalance(node);
  if (balance > 1 && key < node->left->key)
    return rightRotate(node);

  if (balance < -1 && key > node->right->key)
    return leftRotate(node);

  if (balance > 1 && key > node->left->key) {
    
    
    node->left = leftRotate(node->left);
    return rightRotate(node);
  }

  if (balance < -1 && key < node->right->key) {
    
    
    node->right = rightRotate(node->right);
    return leftRotate(node);
  }

  return node;
}

struct Node *minValueNode(struct Node *node) {
    
    
  struct Node *current = node;

  while (current->left != NULL)
    current = current->left;

  return current;
}

// Delete a nodes
struct Node *deleteNode(struct Node *root, int key) {
    
    
  // Find the node and delete it
  if (root == NULL)
    return root;

  if (key < root->key)
    root->left = deleteNode(root->left, key);

  else if (key > root->key)
    root->right = deleteNode(root->right, key);

  else {
    
    
    if ((root->left == NULL) || (root->right == NULL)) {
    
    
      struct Node *temp = root->left ? root->left : root->right;

      if (temp == NULL) {
    
    
        temp = root;
        root = NULL;
      } else
        *root = *temp;
      free(temp);
    } else {
    
    
      struct Node *temp = minValueNode(root->right);

      root->key = temp->key;

      root->right = deleteNode(root->right, temp->key);
    }
  }

  if (root == NULL)
    return root;

  // Update the balance factor of each node and
  // balance the tree
  root->height = 1 + max(height(root->left),
               height(root->right));

  int balance = getBalance(root);
  if (balance > 1 && getBalance(root->left) >= 0)
    return rightRotate(root);

  if (balance > 1 && getBalance(root->left) < 0) {
    
    
    root->left = leftRotate(root->left);
    return rightRotate(root);
  }

  if (balance < -1 && getBalance(root->right) <= 0)
    return leftRotate(root);

  if (balance < -1 && getBalance(root->right) > 0) {
    
    
    root->right = rightRotate(root->right);
    return leftRotate(root);
  }

  return root;
}

// Print the tree
void printPreOrder(struct Node *root) {
    
    
  if (root != NULL) {
    
    
    printf("%d ", root->key);
    printPreOrder(root->left);
    printPreOrder(root->right);
  }
}

int main() {
    
    
  struct Node *root = NULL;

  root = insertNode(root, 2);
  root = insertNode(root, 1);
  root = insertNode(root, 7);
  root = insertNode(root, 4);
  root = insertNode(root, 5);
  root = insertNode(root, 3);
  root = insertNode(root, 8);

  printPreOrder(root);

  root = deleteNode(root, 3);

  printf("\nAfter deletion: ");
  printPreOrder(root);

  return 0;
}

4. AVL树上不同操作的复杂性

插入	删除	查找
O(log n)	O(log n)	O(log n)

5. AVL树应用

在数据库中对大记录进行索引
用于在大型数据库中搜索

参考文档

[1]Parewa Labs Pvt. Ltd.Balanced Binary Tree[EB/OL].https://www.programiz.com/dsa/avl-tree,2020-01-01.