2-3查找树
为了保证查找树的平衡性,我们需要一些灵活性,因此在这里我们允许树中的一个结点保存多个键。
2-结点:含有一个键(及其对应的值)和两条链接,左链接指向的2-3树中的键都小于该结点,右链接指向的2-3树中的键都大于该结点。
3-结点:含有两个键(及值对应的值)和三条链接,左链接指向的2-3树中的键都小于该结点,中链接指向的2-3树中的键都位于该结点的两个键之间,右链接指向的2-3树中的键都大于该结点。
示意图:

一颗完美平衡的2-3查找树中的所有空链接到根结点的距离都是相同的。
查找
要判断一个键是否在树中,我们先将它和根结点中的键比较。如果它和其中的任何一个相等,查找命中。否则我们就根据比较的结果找到指向相应区间的链接,并在其指向的子树中递归地继续查找。如果这是个空链接,查找未命中。

插入
要在2-3树中插入一个新结点,我们可以和二叉查找树一样先进行一次未命中的查找,然后把新结点挂在树的底部。但这样的话树无法保持完美平衡性。我们使用2-3树的主要原因就在于它能够在插入之后继续保持平衡。如果未命中的查找结束于一个2-结点,我们只要把这个2-结点替换为一个3-结点,将要插入的键保存在其中即可。如果未命中的查找结束于一个3-结点,事情就要麻烦一些。
插入可以分为以下几种情况:
1.向一颗只含有一个3-节点的树中插入新键
这棵树唯一的结点中已经没有可插入的空间了。我们又不能把新键插在其空结点上(破坏了完美平衡)。为了将新键插入,我们先临时将新键存入该结点中,使之成为一个4-结点。创建一个4-结点很方便,因为很容易将它转换为一颗由3个2-结点组成的2-3树(将中建移到父节点中去),这棵树既是一颗含有3个结点的二叉查找树,同时也是一颗完美平衡的2-3树,其中所有空链接到根结点的距离都相等。

2.向一个父结点为2-结点的3-结点中插入新键
假设未命中的查找结束于一个3-结点,而它的父结点是一个2-结点。在这种情况下我们需要在维持树的完美平衡的前提下为新键腾出空间。
我们先像刚才一样构造一个临时的4-结点并将其分解,但此时我们不会为中键创建一个新结点,而是将其移动至原来的父结点中。(如图所示)
这次转换也并不影响(完美平衡的)2-3树的主要性质。树仍然是有序的,因为中键被移动到父结点中去了,树仍然是完美平衡的,插入后所有的空链接到根结点的距离仍然相同。

3.向一个父结点为3-结点的3-结点中插入新键
假设未命中的查找结束于一个3-结点,而它的父结点是一个3-结点。
我们再次和刚才一样构造一个临时的4-结点并分解它,然后将它的中键插入它的父结点中。但父结点也是一个3-结点,因此我们再用这个中键构造一个新的临时4-结点,然后在这个结点上进行相同的变换,即分解这个父结点并将它的中键插入到它的父结点中去。
我们就这样一直向上不断分解临时的4-结点并将中键插入更高的父结点,直至遇到一个2-结点并将它替换为一个不需要继续分解的3-结点,或者是到达3-结点的根。

总结:

先找插入结点,若结点为2-结点,则直接插入。如结点为3-结点,则构造一个临时的4-结点,然后将中键移到其父结点中。对父结点亦如此处理。(中键一直往上移,直到找到空位,若到了根结点还是没有空位,则分裂根节点,此时树的高度才会增加)
2-3树插入算法的根本在于这些变换都是局部的:除了相关的结点和链接之外不必修改或者检查树的其他部分。每次变换中,变更的链接数量不会超过一个很小的常数。所有局部变换都不会影响整棵树的有序性和平衡性。
和标准的二叉查找树由上向下生长不同,2-3树的生长是由下向上的。树的构造轨迹:

删除
1.所删除元素位于一个3-结点的叶子结点上
直接删除元素即可,不会影响到整颗树的其它结点结构。
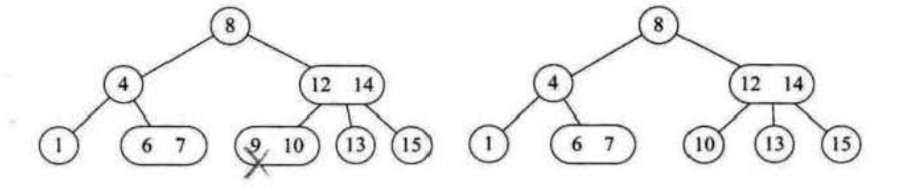
2.所删除的元素位于一个2-结点上
分四种情况:
- 此结点的双亲也是2-点, 拥有一个3-结点的右孩子。只需要左旋,即右孩子的左键成为父结点,父结点成为左结点。

- 此结点的父结点是2- 结点,它的右孩子也是2- 结点

- 此结点的父结点是3-结点

- 当前树是一个满二叉树

3.所删除的元素位于非叶子的分支结点
此时我们通常是将树按中序遍历后得到此元素的前驱或后继元素,考虑让它们来补位即可


特性
优点
2-3树在最坏情况下仍有较好的性能。每个操作中处理每个结点的时间都不会超过一个很小的常数,且这两个操作都只会访问一条路径上的结点,所以任何查找或者插入的成本都肯定不会超过对数级别。
完美平衡的2-3树要平展的多。例如,含有10亿个结点的一颗2-3树的高度仅在19到30之间。我们最多只需要访问30个结点就能在10亿个键中进行任意查找和插入操作。
缺点
我们需要维护两种不同类型的结点,查找和插入操作的实现需要大量的代码,而且它们所产生的额外开销可能会使算法比标准的二叉查找树更慢。
平衡一棵树的初衷是为了消除最坏情况,但我们希望这种保障所需的代码能够越少越好。
红黑树
红黑树(Red Black Tree),简称 R-B Tree。它是一种不严格的平衡二叉查找树,
顾名思义,红黑树中的节点,一类被标记为黑色,一类被标记为红色。除此之外,一棵红黑树还需要满足这样几个要求:
- 根节点是黑色;
- 所有的叶子节点都是黑色的空节点(NIL),也就是说,叶子节点不存储数据;
- 任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的;
- 每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;
如果插入和删除的过程中,违背了红黑树的定义,我们就需要进行调整,调整的过程包含两种基础的操作:左右旋转和改变颜色。
右旋:


左旋:

我们可以通过2-3查找树来理解红黑树,避免记忆红黑树复杂的插入和删除操作。
红黑树背后的思想是用标准的二叉查找树(完全由2-结点构成)和一些额外的信息(替换3-结点)来表示2-3树。
我们将树中的链接分为两种类型:红链接将两个2-结点连接起来构成一个3-结点,黑链接则是2-3树中的普通链接。确切地说,我们将3-结点表示为由一条左斜的红色链接相连的两个2-结点。
这种表示法的一个优点是,对于任意的2-3树,只要对结点进行转换,我们都可以立即派生出一颗对应的红黑树。
一种等价的定义
红黑树的另一种定义是满足下列条件的二叉查找树:
⑴红链接均为左链接。
⑵没有任何一个结点同时和两条红链接相连。
⑶该树是完美黑色平衡的,即任意空链接到根结点的路径上的黑链接数量相同。
一一对应
如果我们将一颗红黑树中的红链接画平,那么所有的空链接到根结点的距离都将是相同的。如果我们将由红链接相连的结点合并,得到的就是一颗2-3树。

相反,如果将一颗2-3树中的3-结点画作由红色左链接相连的两个2-结点,那么不会存在能够和两条红链接相连的结点,且树必然是完美平衡的。
无论我们用何种方式去定义它们,红黑树都既是二叉查找树,也是2-3查找树。
(2-3树的深度很小,平衡性好,效率高,但是其有两种不同的结点,实际代码实现比较复杂。而红黑树用红链接表示2-3树中另类的3-结点,统一了树中的结点类型,使代码实现简单化,又不破坏其高效性。)
颜色表示:
因为每个结点都只会有一条指向自己的链接(从它的父结点指向它),我们将链接的颜色保存在表示结点的Node数据类型的布尔变量color中(若指向它的链接是红色的,那么该变量为true,黑色则为false)。
当我们提到一个结点颜色时,我们指的是指向该结点的链接的颜色。
对于红黑树的插入操作,只需要先看成是插入2-3查找树,然后再转化为红黑树即可。

性质:一颗大小为 N 的红黑树的高度不会超过 2lgN。红黑树的最坏情况是它所对应的 2-3 树中最左边的路径全部是3-结点,而其余均为2-结点。最左边的路径是只包含2-结点的路径长度(~lgN)的两倍。
问:为什么不允许存在红色右链接。
答:红色右链接是可用的,只允许红色左链接存在能够减少可能出现的情况,理解起来更为容易。