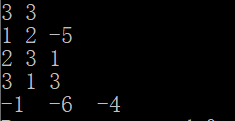说在开头的话：

其实这些最短路径的算法，包括常见的插点，边松弛(因为说他们的名字和他们的算法思想联系不起来，所以我都这样称呼，官方称呼是floyd dijstra)，他们就提出的时候的思想来定义他们的优缺点（比如是否能解决图中存在负权边、能否解决图中存在负权回路），但是编程又不是单纯的实现，如果想避免它的缺陷，完全可以加入自己需要的判定方法来避免它们的缺陷。并不是说，非黑即白，硬给他们划阵营。这样来总结更客观一些，因为我发现编程的时候可以既使用这个算法，又可以避免它本身的缺陷。下面代码纯属本人敲着玩的，一个小时之内连着敲出来的，如有错误的地方，或者值得优化的地方请留言。

几个概念：

负权回路：

在一个图里每条边都有一个值（有正有负)
如果存在一个环（从某个点出发又回到自己的路径），而权且这个环上所有权值之和是负数，那这就是一个负权环，也叫负权回路
存在负权回路的图是不能求两点间最短路的，因为只要在负权回路上不断兜圈子，所得的最短路长度可以任意小。

权值为负数的路径称为负权边，非负权回路可能有负权边。

负权边和负权回路这两个定义要搞清楚。

稠密图和稀疏图：

一个图中，顶点数 n 边数 m

扫描二维码关注公众号，回复： 12733996 查看本文章

当 $n^2$ >>m 时，我们称之为稀疏。

当m相对较大时，我们称之为稠密。

插点法（Floyd算法）

Floyd算法的核心思想就是插点，将所有的点依次插入任意两个点之间，以达到图中任意两个点之间的路径最短。

核心算法：

for(int p=1;p<=n;p++)
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=n; j++)
        {
                if(map[i][p]+map[p][j]<map[i][j])
                {
                    map[i][j]=map[i][p]+map[p][j];
                }
        }
    }

测试程序：

#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<iostream>
using namespace std;
int n,m;
int map[50][50];
int book[50];
int main()
{
    scanf("%d %d",&n,&m);
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=n; j++)
        {
            map[i][j]=99999999;
            if(i==j)
                map[i][j]=0;
        }
    }
    for(int i=1; i<=m; i++)
    {
        int a,b,c;
        scanf("%d %d %d",&a,&b,&c);
        map[a][b]=c;
    }
// 插点法在a+b<|-c|时不能解决负权回路  负权回路会导致路径越来越短，没有最短路径
//3 3
//1 2 2
//2 3 3
//3 1 -6
//for(int q=1;q<=n;q++)
    for(int p=1;p<=n;p++)
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=n; j++)
        {
                if(map[i][p]+map[p][j]<map[i][j])
                {
                    map[i][j]=map[i][p]+map[p][j];
                }
        }
    }


    for(int i=1;i<=n;i++)
    {
         for(int j=1;j<=n;j++)
         {
             printf("%12d ",map[i][j]);
         }
         cout<<"\n";
    }

}

测试结果：

时间复杂度： $O(N^2)$

空间复杂度： $O(N^3)$

适用情况：由于时间/空间复杂度和顶点数量直接相关，所以适用于稠密图，即边越多越划算。

解决问题：多源最短路

附：如果图中存在负权边，并且负权边构成了回路，但是该回路不是负权回路，那插点法就可以求得多源最短路径。如果存在负权回路，经过实验，不能求得最短路径。（如果需要求最短路径，需要自己想办法看看如果避免它的缺陷）

边松弛法（Dijkstra算法）

边松弛法是逐一将源点到各个端点的最短边(一轮只有一条边)插入到其它各个端点之间，用来松弛源点到其它端点的路径，达到源点到各个端点都是最短路径的目的。

核心算法：

    int N=n;
    while(N--)
    {
        minn=99999999;
        for(int i=1; i<=n; i++)
        {
            if(dis[i]<minn && book[i]==0)
            {
                minn=dis[i];
                flag=i;
            }
        }
        book[flag]=1;
        for(int i=1; i<=n; i++)
            if(book[i]==0)
            {
                dis[i]=min(dis[flag]+map[flag][i],map[1][i]);
            }
    }

测试程序：

#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<iostream>
using namespace std;
int n,m;
int map[50][50];
int book[50];
int dis[50];
int minn=99999999;
int main()
{
    scanf("%d %d",&n,&m);
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=n; j++)
        {
            map[i][j]=99999999;
            if(i==j)
                map[i][j]=0;
        }
    }
    for(int i=1; i<=m; i++)
    {
        int a,b,c;
        scanf("%d %d %d",&a,&b,&c);
        map[a][b]=c;
    }

    for(int i=1; i<=n; i++)
    {
        dis[i]=map[1][i];
    }


//3 3
//1 2 -10
//2 3 -3
//3 1 -5
    int flag=0;
    int N=n;
    while(N--)
    {
        minn=99999999;

        for(int i=1; i<=n; i++)
        {
            if(dis[i]<minn && book[i]==0)
            {
                minn=dis[i];
                flag=i;
            }
        }
        book[flag]=1;
        for(int i=1; i<=n; i++)
            if(book[i]==0)
            {
                dis[i]=min(dis[flag]+map[flag][i],map[1][i]);
            }
    }

    for(int i=1;i<=n;i++)
        cout<<dis[i]<<"   ";
    cout<<endl;
}

测试结果：

空间复杂度 O(M) 我的时间复杂度O（ $\large n^2$ ）

时间复杂度O((M+N)logN) 我的空间复杂度O（ $\large n^2$ ）

适用于稠密图（顶点一定的情况下，边越多越划算）

存在负权边的情况下，不能算出最短路径 我经过实验发现能算出来，不只是负权边，负权回路都没问题。

解决问题：单源最短路

附：

N：图中顶点个数

M：图中边的个数

在这样的时间复杂度下，边越多才越划算，如果像算法导论写的，将时间复杂度用堆优化到O((M+N)logN)，那边多了，M比N可能大的多，根据边与顶点的关系，边最多能达到 $\large 1/2(n(n-1))$ ，时间复杂度反而不如我的。

点松弛法（Bellman_Ford算法）

它的思想同样是边松弛（我认为点松弛法更符合它的特点），但不是逐一将源点到各个端点的最短路径（一轮只有一条边）用来松弛源点到其它各个顶点的路径。而是将源点的出边（一轮，可能有多条）作为最短路径，松弛到其它各个顶点的路径，而后，将这些邻点的出边为最短路径，松弛其它顶点，直到源点到所有顶点都达到了最短路径。

核心算法：

for(int r=1; r<=n-1; r++)
{
        for(int i=1; i<=m; i++)
        {
            dis[v[i]]=min(dis[v[i]],dis[u[i]]+w[i]);
        }
}

测试程序：

#include<stdio.h>
#include<string.h>
#include<iostream>
using namespace std;
int u[100],v[100],w[100];
int dis[100];
int book[100];
int flag;
int main()
{
    int n,m;
    scanf("%d %d",&n,&m);
    for(int i=1; i<=m; i++)
        scanf("%d %d %d",&u[i],&v[i],&w[i]);

    for(int i=1; i<=m; i++)
    {
        if(i==1)
            dis[i]=0;
        else
            dis[i]=99999999;
    }

    for(int r=1; r<=n-1; r++)
    {
        flag=0;
        for(int i=1; i<=m; i++)
        {
            dis[v[i]]=min(dis[v[i]],dis[u[i]]+w[i]);
        }
        for(int i=1; i<=n; i++)
        {
            if(book[i]!=dis[i])
            {
                flag=1;
                break;
            }
        }
        if(flag==0)
            break;
        for(int i=1; i<=n; i++)
        {
            book[i]=dis[i];
        }
    }
    for(int i=1; i<=m; i++)
    {
        if(dis[v[i]]>dis[u[i]]+w[i])
        {
            dis[v[i]]=dis[u[i]]+w[i];
            flag=1;
        }
    }
    if(flag==1)
        cout<<"存在负权回路"<<endl;
    else
        for(int i=1; i<=n; i++)
        {
            cout<<dis[i]<<"  ";
        }

}

空间复杂度 O(M)

时间复杂度O(NM)

和边有关，顶点一定，边越少，越划算。

负权边可以正常求得最短路径，负权回路甚至可以检测出来。

用来解决单源最短路问题。

队列加速下的点松弛法（SPFA（Shortest Path Faster Algorithm)）

spfa是队列优化下的bellman_ford算法,在bellman_ford算法中，每实施一次松弛操作，就会有得到一些源点到某些顶点之间的最短路，此后这些最短路就不会发生改变，不再受后续松弛操作的影响。为了去掉多余的操作，每次仅对最短路值（源点到该顶点）发生变化的顶点的出边进行松弛操作即可。

测试程序

#include<stdio.h>
#include<string.h>
#include<iostream>
using namespace std;
int u[100],v[100],w[100];
int dis[100];
int book[100];
int que[100];
int head,tail;
int first[100],next[100];
int flag;
int main()
{
    int n,m;
    scanf("%d %d",&n,&m);
    for(int i=1; i<=m; i++)
    {
        scanf("%d %d %d",&u[i],&v[i],&w[i]);
        first[i]=-1;
        next[i]=-1;
    }

    for(int i=1; i<=m; i++)
    {
        if(first[u[i]]==-1)
        {
            first[u[i]]=i;
        }
        else
        {
            next[i]=first[u[i]];
            first[u[i]]=i;
        }
    }
    for(int i=1; i<=m; i++)
    {
        if(i==1)
            dis[i]=0;
        else
            dis[i]=99999999;
    }


    int sum=0;
    int t;
    que[tail++]=first[1];
      while(head<tail)
    {
        t=que[head];
        while(t!=-1)
        {
            if(dis[v[t]]>dis[u[t]]+w[t])
            {

                if(book[v[t]]==0)
                {
                    que[tail++]=first[v[t]];
                }
                dis[v[t]]=dis[u[t]]+w[t];
            }
            t=next[t];
        }
        head++;
        int temp=head;
        for(temp; temp<tail; temp++)
        {
            book[que[temp]]=1;
            cout<<que[temp]<<endl;
        }

    }



    for(int i=1; i<=n; i++)
    {
        cout<<dis[i]<<"  ";
    }
}

测试结果：

空间复杂度：O(M)

时间复杂度：<O(NM)

和边关系密切，在顶点数量一定的情况下，边越少越划算，适用于稀疏图。

负权边可以正常求得最短路径，负权回路甚至可以检测出来（我目前还没想法可以检测出来负权回路）。

用来解决单源最短路问题。

附：上面我写的程序当存在负权边时可以求出最短路径，负权回路就不行了。所以算法和解决的问题其实没有什么关系，和以什么想法编程有关系。

存在负权边时：

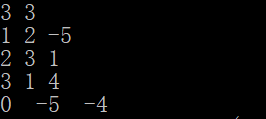
存在负权回路时：

几种简单的的最短路算法：插点法、边松弛法、点松弛法、队列加速下的点松弛法

插点法（Floyd算法）

边松弛法（Dijkstra算法）

点松弛法（Bellman_Ford算法）

队列加速下的点松弛法（SPFA（Shortest Path Faster Algorithm)）

猜你喜欢