在基于深度学习的图像分割领域,基于Encoder-Decoder框架是一种非常经典的模型设计。在这种框架下,模型可以看作由两部分组成:编码器模块Encoder和解码器模块Decoder. 编码器模块负责提取特征,采用卷积和池化操作逐步缩小特征图并捕获更高级的语义信息;解码器模块基于上采样操作逐步恢复空间信息。
下图是SegNet论文中体现Encoder-Decoder框架的示意图。
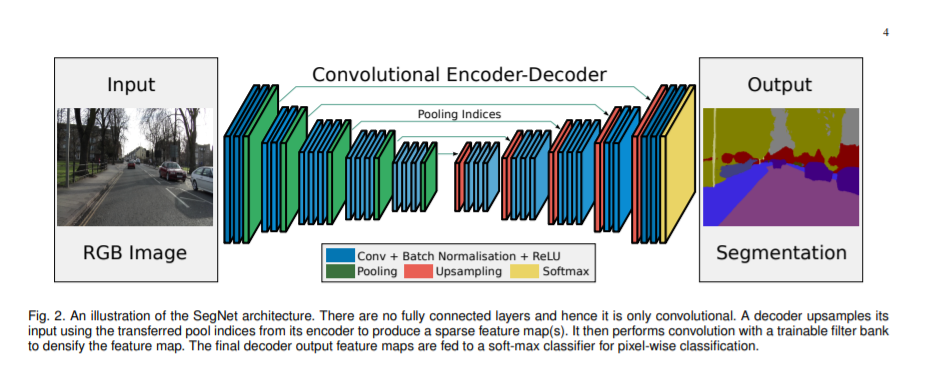
上文提到,解码器模块基于上采样来不断恢复空间信息。本节内容即关注上采样这一操作,介绍在不同的语义分割网络中常用的上采样方法。
一、Bilinear interpolation 双线性插值
1.1 线性插值
线性插值是一种较为简单的插值方法,其插值函数为一次多项式。线性插值,在各插值节点上插值的误差为0。

已知数据 ( x 1 , y 1 ) (x_1, y_1) (x1,y1)和 ( x 2 , y 2 ) (x_2, y_2) (x2,y2), 计算在 [ x 1 , x 2 ] [x_1, x_2] [x1,x2]区间内某一位置 x x x在直线上的 y y y值。
已知:
y − y 1 y 2 − y 1 = x − x 1 x 2 − x 1 \frac {y - y_1} {y_2 - y_1} = \frac {x - x_1} {x_2 - x_1} y2−y1y−y1=x2−x1x−x1
计算公式如下:
y = x 2 − x x 2 − x 1 ∗ y 1 + x − x 1 x 2 − x 1 ∗ y 2 y = \frac {x_2 - x} {x_2 - x_1} *y_1 + \frac {x - x_1} {x_2 - x_1} *y_2 y=x2−x1x2−x∗y1+x2−x1x−x1∗y2
1.2 双线性插值
双线性插值,又称为双线性内插。在数学上,双线性插值是有两个变量的插值函数的线性插值扩展,其核心思想是在两个方向分别进行一次线性插值。

设有一个表达式未知的函数 f ( x , y ) f(x,y) f(x,y),
已知四个点 ( x 1 , y 1 ) (x_1, y_1) (x1,y1)、 ( x 1 , y 2 ) (x_1, y_2) (x1,y2)、 ( x 2 , y 1 ) (x_2, y_1) (x2,y1)、 ( x 2 , y 2 ) (x_2, y_2) (x2,y2)在 f ( x , y ) f(x,y) f(x,y)的值,
求在点 ( x , y ) (x,y) (x,y)位置上 f ( x , y ) f(x,y) f(x,y)的值。

第一阶段,我们先在 x x x方向上进行两次线性插值,分别在点 ( x 1 , y 1 ) (x_1, y_1) (x1,y1)和 ( x 2 , y 1 ) (x_2, y_1) (x2,y1)之间插入点 ( x , y 1 ) (x, y_1) (x,y1),和在点 ( x 1 , y 2 ) (x_1, y_2) (x1,y2)和 ( x 2 , y 2 ) (x_2, y_2) (x2,y2)之间插入点 ( x , y 2 ) (x, y_2) (x,y2)。
f ( x , y 1 ) ≈ x 2 − x x 2 − x 1 ∗ f ( x 1 , y 1 ) + x − x 1 x 2 − x 1 ∗ f ( x 2 , y 1 ) f(x,y_1) \approx \frac {x_2 - x}{x_2 - x_1} * f(x_1, y_1) + \frac {x - x_1}{x_2 - x_1} * f(x_2, y_1) f(x,y1)≈x2−x1x2−x∗f(x1,y1)+x2−x1x−x1∗f(x2,y1)
f ( x , y 2 ) ≈ x 2 − x x 2 − x 1 ∗ f ( x 1 , y 2 ) + x − x 1 x 2 − x 1 ∗ f ( x 2 , y 2 ) f(x,y_2) \approx \frac {x_2 - x}{x_2 - x_1} * f(x_1, y_2) + \frac {x - x_1}{x_2 - x_1} * f(x_2, y_2) f(x,y2)≈x2−x1x2−x∗f(x1,y2)+x2−x1x−x1∗f(x2,y2)
第二阶段,我们在 y y y方向上进行一次线性插值,即在点 ( x , y 1 ) (x, y_1) (x,y1)和 ( x , y 2 ) (x, y_2) (x,y2)之间插入点 ( x , y ) (x, y) (x,y)。
f ( x , y ) ≈ y 2 − y y 2 − y 1 ∗ f ( x , y 1 ) + y − y 1 y 2 − y 1 ∗ f ( x , y 2 ) f(x,y) \approx \frac {y_2 - y}{y_2 - y_1} * f(x, y_1) + \frac {y - y_1}{y_2 - y_1} * f(x, y_2) f(x,y)≈y2−y1y2−y∗f(x,y1)+y2−y1y−y1∗f(x,y2)
以上就是双线性插值二个阶段的执行过程。值得注意的是:双线性插值的最终结果与执行线性插值的顺序无关,即先在 y y y方向插值,然后在 x x x方向插值也会得到相同的结果。
1.3 基于PyTorch 和 OpenCV的Bilinear实现
一、引入必要的库
import torch
import numpy as np
import cv2
from PIL import Image
import torch.nn.functional as F
二、设置输入图像
# 设置输入数据,形式为[N × C × H × W]
image = np.array(range(1, 5)).reshape(1, 1, 2, 2)
print(image)
[[[[1 2]
[3 4]]]]
三、基于PyTorch 实现Bilinear
pytorch_aligned_output = F.interpolate(torch.Tensor(image), scale_factor=2, mode='bilinear', align_corners=True)
print(pytorch_aligned_output)
tensor([[[[1.0000, 1.3333, 1.6667, 2.0000],
[1.6667, 2.0000, 2.3333, 2.6667],
[2.3333, 2.6667, 3.0000, 3.3333],
[3.0000, 3.3333, 3.6667, 4.0000]]]])
pytorch_aligned_output = F.interpolate(torch.Tensor(image), scale_factor=2, mode='bilinear', align_corners=False)
print(pytorch_aligned_output)
tensor([[[[1.0000, 1.2500, 1.7500, 2.0000],
[1.5000, 1.7500, 2.2500, 2.5000],
[2.5000, 2.7500, 3.2500, 3.5000],
[3.0000, 3.2500, 3.7500, 4.0000]]]])
注意: 关于实现方法中属性align_corners,
- 当align_corners=True时,像素被视为点的网格。角点对齐。
- 当align_corners=False时,像素被视为1x1区域。区域边界(而不是其中心)是对齐的。
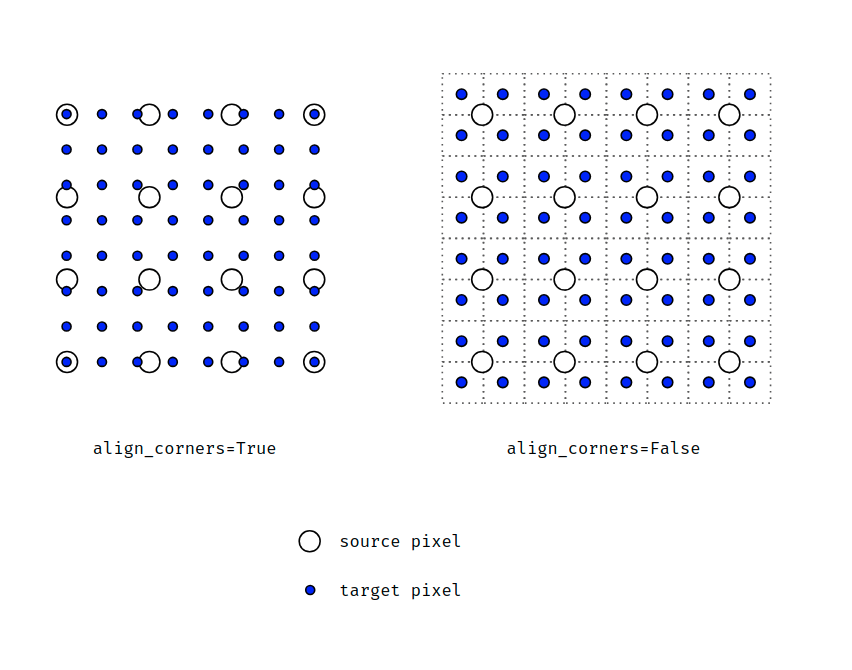
四、基于OpenCV 实现Bilinear
cv2_output = cv2.resize(image[0, 0].astype(np.float32), (4, 4), interpolation=cv2.INTER_LINEAR)
print(cv2_output)
[[1. 1.25 1.75 2. ]
[1.5 1.75 2.25 2.5 ]
[2.5 2.75 3.25 3.5 ]
[3. 3.25 3.75 4. ]]
我们看到这个结果和PyTorch实现中align_corners=False一致。可见OpenCV中实现Bilinear是直接按照align_corners=False处理的。
1.4 特点分析
不需要学习,运算速度快。
二、Un-pooling 反池化
2.1 原理描述
池化操作是通过在输入特征图上从上到下、从左到右地滑动窗口,并对每个窗口里的内容执行一个池化函数(最大值、均值)来完成整个池化过程。下图是对一个 5 ∗ 5 5*5 5∗5的输入特征图采用 3 ∗ 3 3*3 3∗3的池化核进行池化,得到 3 ∗ 3 3*3 3∗3的输出特征图的过程。
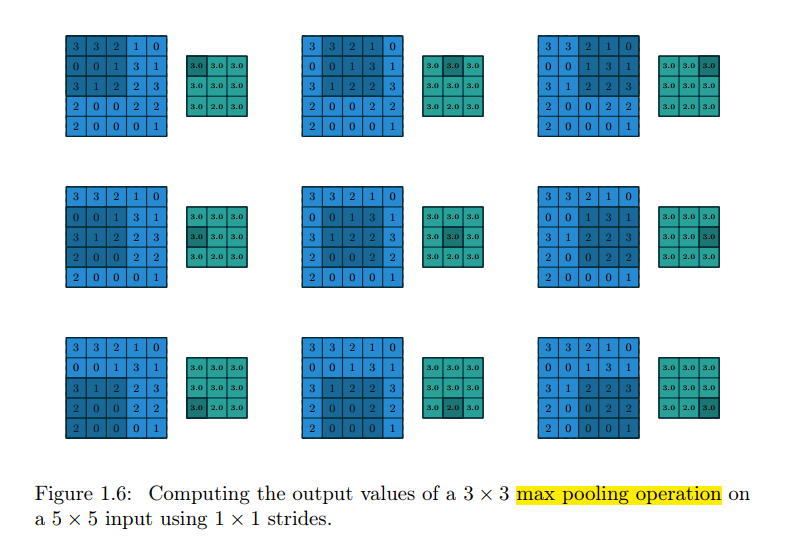
那么反池化的思路就是基于 3 ∗ 3 3*3 3∗3的输出特征图,直接按照池化操作的位置还原回去。这里需要注意的是,我们需要在池化过程中记录每个窗口里最大值的位置,以上图为例,即最大值的索引位置为 [ 0 , 1 , 8 , 10 , 8 , 8 , 10 , 12 , 14 ] [0,1,8,10,8,8,10,12,14] [0,1,8,10,8,8,10,12,14], 那么我们就可以基于输出特征图和索引位置,还原出输入特征图。

2.2 PyTorch 实现max_unpool2d
注:使用的库和本文第一节的引入库相同
一、设置输入图像
# 设置输入数据为二维数据,形式为[N × C × H × W]
image = np.array([
[3,3,2,1,0],
[0,0,1,3,1],
[3,1,2,2,3],
[2,0,0,2,2],
[2,0,0,0,1]
])
image = image.reshape((1,1,5,5))
print(image)
[[[[3 3 2 1 0]
[0 0 1 3 1]
[3 1 2 2 3]
[2 0 0 2 2]
[2 0 0 0 1]]]]
二、最大池化,同时记录索引
res,indices = F.max_pool2d(torch.Tensor(image), kernel_size=3, stride=1, return_indices=True)
print(res)
print(indices)
tensor([[[[3., 3., 3.],
[3., 3., 3.],
[3., 2., 3.]]]])
tensor([[[[ 0, 1, 8],
[10, 8, 8],
[10, 12, 14]]]])
三、反池化
unpool_res = F.max_unpool2d(res, indices, kernel_size=3, stride=1)
print(unpool_res)
tensor([[[[3., 3., 0., 0., 0.],
[0., 0., 0., 3., 0.],
[3., 0., 2., 0., 3.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]]]])
2.3 特点分析
- 同样不需要学习
- 目前应用的很少,据了解仅在SegNet网络上使用。可在文末参考文献查看SegNet源码实现
三、Transposed convolution 转置卷积
3.1 原理描述
理解转置卷积之前,我们先看看卷积的实现过程。
在框架进行卷积操作实现中,为了更快的执行速度,卷积运算可以转换为矩阵运算进行处理。
具体过程为:将 4 ∗ 4 4*4 4∗4的输入矩阵 A A A展平为一个16维度的向量,通过矩阵运算 C A = B CA = B CA=B,输出一个4维的向量 B B B,最后将 B B B再重塑为 2 ∗ 2 2*2 2∗2的矩阵。下图是卷积核 C C C的稀疏矩阵表示。
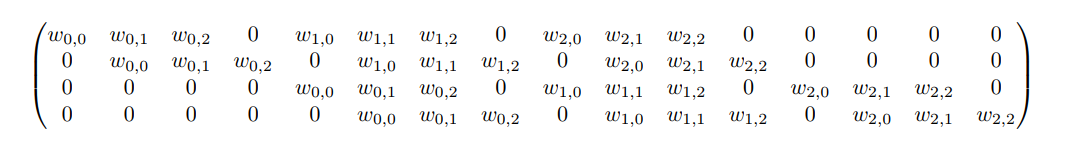
转置卷积正是相反的操作,将一个4维度的向量作为输入,卷积核的形式是大小为 16 ∗ 4 16*4 16∗4的 C T C^T CT,可以输出一个16维的向量。
除了上面介绍的方式,转置卷积操作也可以使用直接卷积来实现。
已知卷积过程:对于一个大小为 i = 4 ∗ 4 i=4*4 i=4∗4的输入,可以使用卷积核 k = 3 ∗ 3 , s t r i d e = 1 , p a d d i n g = 0 k=3*3,stride=1,padding=0 k=3∗3,stride=1,padding=0, 通过公式 o = ( i − k + 2 ∗ p ) / s + 1 o = (i-k+2*p)/s + 1 o=(i−k+2∗p)/s+1,可以得到输出大小为 2 ∗ 2 2*2 2∗2。
对于转置卷积过程:一个大小为 i ’ = 2 ∗ 2 i^{’}=2*2 i’=2∗2的输入,可以使用卷积核 k ′ = k = 3 ∗ 3 , p a d d i n g ′ = k − p a d d i n g − 1 = 2 , s t r i d e ′ = 1 k^{'}=k=3*3,padding^{'}=k-padding-1=2,stride^{'}=1 k′=k=3∗3,padding′=k−padding−1=2,stride′=1, 同样根据公式可以得到输出大小为 4 ∗ 4 4*4 4∗4。
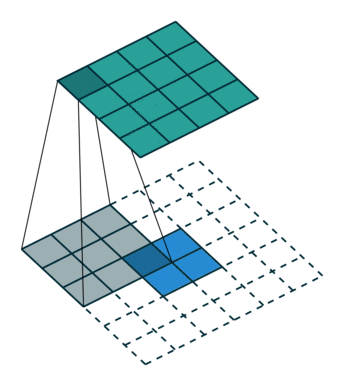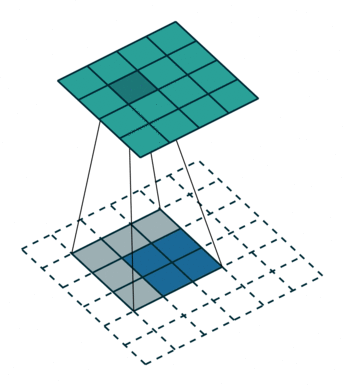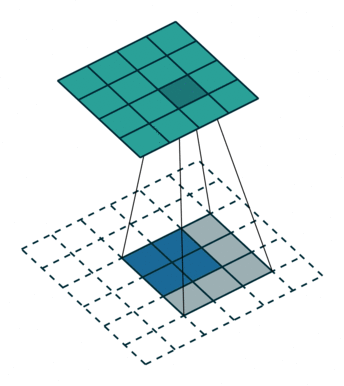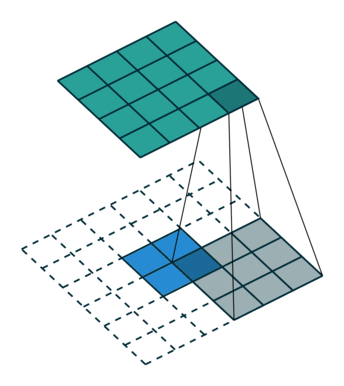
上述例子里 s t r i d e = 1 stride=1 stride=1, 对于 s t r i d e > 1 stride>1 stride>1的情况,举例如下:
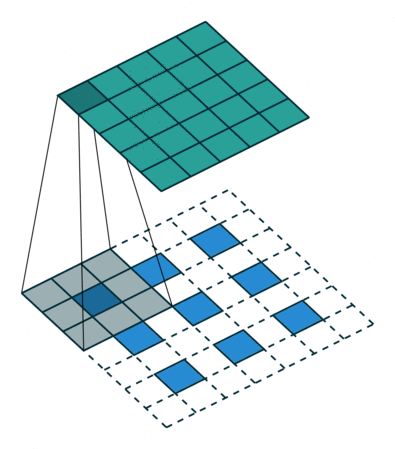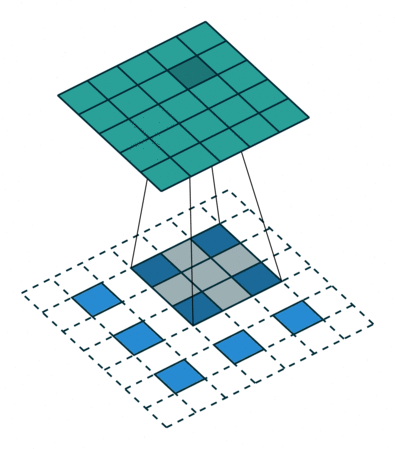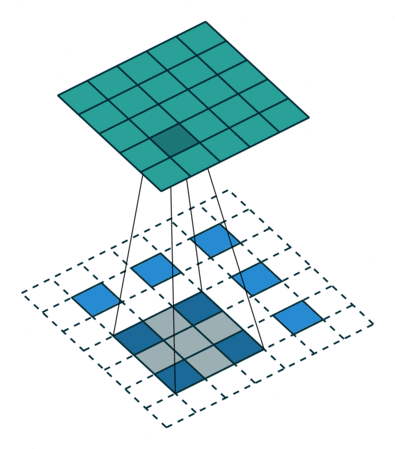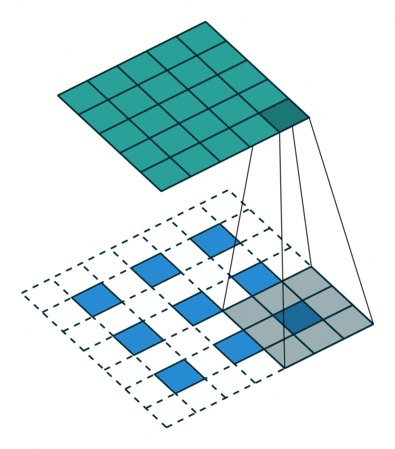
对于一个大小为 i = 5 ∗ 5 i=5*5 i=5∗5的输入,可以使用卷积核 k = 3 ∗ 3 , s t r i d e = 2 , p a d d i n g = 1 k=3*3,stride=2,padding=1 k=3∗3,stride=2,padding=1, 通过公式 o = ( i − k + 2 ∗ p ) / s + 1 o = (i-k+2*p)/s + 1 o=(i−k+2∗p)/s+1,可以得到输出大小为 3 ∗ 3 3*3 3∗3。
对于转置卷积过程:一个大小为 i ’ = 3 ∗ 3 i^{’}=3*3 i’=3∗3的输入,首先进行内部扩展得到 i " = i ’ + ( i ’ − 1 ) ∗ ( s t r i d e − 1 ) = s t r i d e ( i ’ − 1 ) + 1 = 5 i^{"}=i^{’}+(i^{’}-1)*(stride-1)=stride(i^{’}-1)+1=5 i"=i’+(i’−1)∗(stride−1)=stride(i’−1)+1=5。可以使用卷积核 k ′ = k = 3 ∗ 3 , p a d d i n g ′ = k − p a d d i n g − 1 = 1 , s t r i d e ′ = 1 k^{'}=k=3*3,padding^{'}=k-padding-1=1,stride^{'}=1 k′=k=3∗3,padding′=k−padding−1=1,stride′=1, 同样根据公式可以得到输出大小为 5 ∗ 5 5*5 5∗5。
3.2 特点分析
- 需要学习
- 在图像分割中应用很广泛
写在最后的话
欢迎关注我的个人公众号,定期原创技术分享。公众号后台回复“图像分割”,获取本文涉及到的经典论文。
愿与各位一起进步!

参考文献
- https://discuss.pytorch.org/t/what-we-should-use-align-corners-false/22663/9
- https://zhuanlan.zhihu.com/p/87572724
- https://github.com/delta-onera/segnet_pytorch/blob/master/segnet.py#L108
- https://blog.csdn.net/tsyccnh/article/details/87357447
- https://distill.pub/2016/deconv-checkerboard/
- https://www.cnblogs.com/yssongest/p/5303151.html
- https://zhuanlan.zhihu.com/p/81947612
- https://zhuanlan.zhihu.com/p/59044838