数论入门篇

欧几里得定理

$gcd(a,b)=gcd(a\%b,b)$(a>=b)
给出简单证明:
可以知道$gcd(a,b)<=b且为b的因子$
$a=mb+r$容易得到左边的mb部分一定可以被b的所有因子整除,所以不会对结果造成影响，所以得证对于a>=b,$gcd(a,b)=gcd(a\%b,b)$。
递归求解,当b=0时返回a即可。

拓展性质:对于a>=b,$gcd(a,b)=gcd(a-b,b)$=$gcd(a+b,b)$
即$gcd(a+k\ast b,b)=gcd(a,b)$,k为整数

裴蜀定理(贝祖定理)

$ax+by=gcd(a,b)$
对于$a$,$b$的$gcd(a,b)$,一定存在系数x和y，使得:
$ax+by=gcd(a,b)$

拓展欧几里得定理

对贝祖定理系数的求解过程称为拓展欧几里得定理

ll exgcd(ll a,ll b,ll &x,ll &y)
{
    
    
    if(b==0)
    {
    
    
        x=1;
        y=0;
        return a;
    }
    else {
    
    
        ll g=exgcd( b, a % b, y, x);
        y -= a / b * x;
        return g;
    }
}

证明:
$a{x}_1+b{y}_1=gcd(a,b)$
$b{x}_2+(a\%b)y_2=gcd(a,b)$
联立两个等式可得：
$a\cdot x_1+b\cdot y_1$
$=b\cdot x_2+(a\%b)y_2$
$=b\cdot x_2+(a-a/b\cdot b)y_2$
$=a\cdot y_2+b\cdot (x_2-a/b\cdot y_2)$
可以得到:
$x_1=y_2$
$y_1=x_2-a/b\cdot y_2$

定理的一些基本应用
1.求$x$模$p$的逆元
2.关于系数的变化
对于 $ax+by=gcd(a,b)$
两边同除以$gcd(a,b)$,
则a与b变成了素数p和q,
$px+qy=1$
系数x,y可以随意变动,
$x$每增大$q$,$y$就减少$p$,反之亦然。

算数基本定理：

一个数可被唯一地表示成若干个素数的乘积。
$x=p_1^{cn{t}_1}\ast p_2^{cn{t}_2}\ast p_3^{cn{t}_3}\ast \cdots \ast p_n^{cn{t}_n}$
$cn{t}_i$表示x分解后的乘积表达式中有$cn{t}_i$个$p_i$.
定理的一些基本应用
1.求出x的因子个数
$factorCnt=(cn{t}_1+1)\ast (cn{t}_2+1)\ast \cdots \ast (cn{t}_n+1)$
2.更好地理解$gcd(最大公因数)$
$gcd(a,b)=p_1^{min(cnt{a}_1,cnt{b}_1)}\ast p_2^{min(cnt{a}_2,cnt{b}_2)}\ast \cdots \ast p_n^{min(cnt{a}_n,cnt{b}_n)}$
3.更好地理解$lcm(最小公倍数)$
$lcm(a,b)=p_1^{max(cnt{a}_1,cnt{b}_1)}\ast p_2^{max(cnt{a}_2,cnt{b}_2)}\ast \cdots \ast p_n^{max(cnt{a}_n,cnt{b}_n)}$

费马小定理

如果p是一个质数，而整数a不是p的倍数，那么$1.$$a^{p}modp=$$amodp$.
$2.$$a^{p-1}modp$$=1modp$.
应用:
1.求一个数x模p的逆元y
$y=x^{p-2}$
证明:
$$\begin{gathered} x\ast y \\ =x\ast x^{p-2} \\ =x^{p-1}modp \\ =1(此处由费马小定理得出) \end{gathered}$$
因为取模运算后的结果已经不能简单地用除法，所以我们引入了乘法逆元的概念,即你如果在模p条件下想除以一个数,只能用乘以它的逆元代替。
证明可以看下文的完全剩余系

互质的判断

若$gcd(x,y)=1，表明x,y互质$
拓展性质:
若$x和y互质，$
1.$gcd(x+y,x\ast y)=1$
证明：x和y互质表明它们没有共同的质因子,另$z=x\ast y$，显然z具有x,y所有的质因子。
而$x+y$要存在至少一个x或y的因子的条件是:$x+y$能够整除这些质因子,但因为$x+y$合并时,x和y没有一个共同的质因数,所以相加后这些质数并未能保留，全部变成了别的质因数。所以,$gcd(x+y,x\ast y)=1$.

欧拉函数

定义：对于正整数n,欧拉函数φ(n)是小于n的正整数中与n互质的数的数目.
1.对于素数p,$\phi (p)=p-1$
2.对于素数p,$\phi (p^k)=p^k-p^{k-1}$
3.若$p_1$与$p_2$互质, 那么$\phi (p_1{p}_2)=\phi (p_1)\phi (p_2)$
证明：如果a与p1互质(a<p1)，b与p2互质(b<p2)，c与p1p2互质(c<p1p2)，则c与数对 (a,b) 是一一对应关系。由于a的值有φ(p1)种可能，b的值有φ(p2)种可能，则数对 (a,b) 有$\phi (p1)\phi (p2)$种可能，而c的值有$\phi (p1p2)$种可能，所以$\phi (p1p2)$就等于$\phi (p1)\phi (p2)$。
4.对于一个有多个质因子的数x,
$x(x=p_1^{k_1}{p}_2^{k_2}\cdots p_n^{k_n})$,
由第三个性质可得：
$\phi (x)=\phi (p_1^{k_1})\phi (p_2^{k_2})\cdots \phi (p_n^{k_n})$
由第四个性质可得(n为x不同质因数的个数)：
$\phi (p_1^{k_1})\phi (p_2^{k_2})\cdots \phi (p_n^{k_n})$$$\begin{gathered} =p_1^{k_1}(1-\frac{1}{p_1})p_2^{k_2}(1-\frac{1}{p_2})\cdots p_n^{k_n}(1-\frac{1}{p_n}) \\ =p_1^{k_1}{p}_2^{k2}\cdots p_n^{k_n}(1-\frac{1}{p_1})(1-\frac{1}{p_2})\cdots (1-\frac{1}{p_n}) \\ =x(1-\frac{1}{p_1})(1-\frac{1}{p_2})\cdots (1-\frac{1}{p_n}) \\ =x{\prod }_{i=1}^n(1-\frac{1}{p_i}) \end{gathered}$$

同余关系

$加法$
1.如果$a\equiv b且c\equiv d$，那么$a+c\equiv b+d(modm)$
$减法$
2.如果$a\equiv b且c\equiv d$，那么$a-c\equiv b-d(modm)$
$乘法$
3.如果$a\equiv b且c\equiv d$，那么$ac\equiv bd(modm)$
4…如果$a\equiv b且c\equiv d$，那么$a^n\equiv b^n(modm)$
$除法$
只有在满足d与m互质的情况下
$ad\equiv bd(modm)$等价于$a\equiv b(modm)$,$d\ne 0$
证明:
寻找系数$d^{\prime }和m^{\prime }$,使得$d{d}^{\prime }+m^{\prime }m=1(d和m互质,gcd(d,m)=1)$,
那么$ad\equiv bd⟺ad{d}^{\prime }\equiv bd{d}^{\prime }$
因为$d{d}^{\prime }=1-m{m}^{\prime }$
所以$a\equiv b$

模数变化

$ad\equiv bd(modmd)$等价于$a\equiv b(modm)$
$ad\equiv bd(modm)$等价于$a\equiv b(mod\frac{m}{gcd(d,m)})$
证明：$d{d}^{\prime }+m{m}^{\prime }=gcd(d,m)$,
这就给出同余式
$a\ast gcd(d,m)\equiv b\ast gcd(d,m)(modm)$
$\to a\equiv b(mod\frac{m}{gcd(d,m)})$

$a\equiv b(modmd)$等价于$a\equiv b(modm)$,$d为整数$

如果$m\perp n(互质)$,
$a\equiv b(modmn)$$⟺a\equiv b(modm)并且a\equiv b(modn)$

中国剩余定理

找到一个满足以下条件并最小的$X$
对于任意i都满足,$Xmod{m}_i$=$a_i$$(1<=i<=n)$
要求$m_i$之间互质
首先考虑一个周期性,即找到一个可行解,该如何处理使得解更小呢?不断减去周期T即可。
$T={\prod }_{i=1}^n{m}_i$
对于X，我们不妨考虑找到一个组合使得X=$\sum x_i$
$x_i$满足条件$xi\%m_i$=$a_i并且(T/m_i)|x_i$，则这个$x_i$不会对其他$x$造成影响。
怎么找到这个$x_i$呢？
1.求出$T/m_i$模$m_i$下的逆元$p$
2.令$x_i$=$T/m_i$*p,则乘积模$m_i$为1
3.再把$x_i$乘以$a_i$即可
思考：为什么要求$m_i$之间互质呢？
如果$m_i$之间不互质,那么周期T就不为这个。
思考：那么如果$m_i$之间不互质该怎么办呢？
把非互质的方程组消去,合并成一个。
用拓展欧几里得消去其他m非互质的方程,合并后的$mod$为$lcm(m_i,m_j)$

大佬博客

欧拉定理

若$gcd(a,m)=1,则a^{\phi (m)}\equiv 1(modm)$

拓展欧拉定理（欧拉降幂公式）

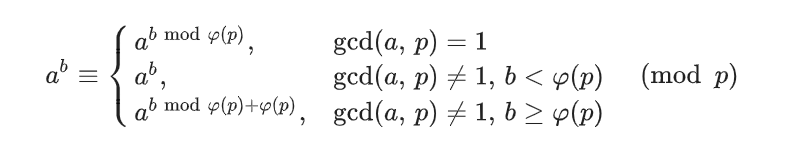
$若gcd(a,p)=1,那么a^b=a^{bmod\phi (p)}$
$否则,若b>=\phi (p),a^b=a^{bmod\phi (p)+\phi (p)}$
$若b<\phi (p),a^b=a^b$

乘法逆元的几种求法

限制条件
1.拓展欧几里得(要求a与m互质)
2.费马小定理(要求a与p互质,并且p为质数)

一些数学术语(摘自百度百科)

剩余类
设模为n，则根据余数可将所有的整数分为n类，把所有与整数a模n同余的整数构成的集合叫做模n的一个剩余类，记作[a]。并把a叫作剩余类[a]的一个代表元。

完全剩余系
在模n的剩余类中各取一个元素，则这n个数就构成了模n的一个完全剩余系。
简化剩余系
简化剩余系(reduced residue system)也称既约剩余系或缩系，是m的完全剩余系中与m互素的数构成的子集，如果模m的一个剩余类里所有数都与m互素，就把它叫做与模m互素的剩余类。
在与模m互素的全体剩余类中，从每一个类中各任取一个数作为代表组成的集合，叫做模m的一个简化剩余系。
例如:
模5的一个简化剩余系是1,2,3,4,模10的一个简化剩余系是1,3,7,9,模18的一个简化剩余系是1,5,7,11,13,17

一些引理
1.若a,b,c为任意三个整数,m为正整数,且$(m,c)=1$,则当$ac\equiv bc(modm)$时,有
$a\equiv b(modm)$
证明：
上式等价于:
$c(a-b)\equiv 0(modm)$
$\because (m,c)=1$
$\therefore a-b\equiv 0(modm)$
$\therefore a\equiv b(modm)$
2.设$m$是一个整数且$m>1$，$b$是一个整数且$(m,b)=1$。
如果$a[1],a[2],a[3],a[4],\dots a[m]$是模m的一个完全剩余系，
则$b\cdot a[1],b\cdot a[2],b\cdot a[3],b\cdot a[4],\dots b\cdot a[m]$也构成模m的一个完全剩余系。
证明采用反证法:
如若存在$b\cdot a[i]\equiv b\cdot a[j]$,那么$b(a[i]-a[j])\equiv 0(modm)$
$又因为(b,m)=1$,则$a[i]\equiv a[j](modm)$,与条件矛盾。
作用
证明费马小定理:如果$(a,p)=1$($p$为素数),则$a^{p-1}=1$
过程：构造素数p的完全剩余系
P = { 1 , 2 , 3 , … , p − 1 } P=\{1,2,3,\dots,p-1\} P={ 1,2,3,…,p−1}
又$(a,p)=1$,那么根据引理2,
Q = { a , 2 a , 3 a , … , ( p − 1 ) a } Q=\{a,2a,3a,\dots,(p-1)a\} Q={ a,2a,3a,…,(p−1)a}也为p的完全剩余系
根据完全剩余系的性质：
$1\ast 2\ast 3\ast \cdots \ast (p-1)\equiv a\cdot 2a\cdot 3a\cdot \dots \cdot (p-1)a(modp)$
$(p-1)!\equiv (p-1)!\cdot a^{p-1}(modp)$
消去$(p-1)!$,得到$a^{p-1}\equiv 1(modp)$

卢卡斯定理

Lucas定理是用来求 $c(n,m)modp$
C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p

ll lucas(ll n,ll m,ll mod)
{
    
    
    if(!m)return 1;
    return C(n%mod,m%mod,mod)*lucas(n/mod,m/mod,mod)%mod;
}