文章目录
尽量两天弄完
线性代数
内积就是两个向量的模×余弦
A ∗ B = ∣ A ∣ ∗ ∣ B ∣ ∗ cos ( α ) A * B=|A| *|B| * \cos (\alpha) A∗B=∣A∣∗∣B∣∗cos(α)
推荐系统评价
覆盖率是指模型能够在测试集上推荐的项目占训练数据的百分比。
metric 买
matrix 美
Evaluation Metrics for Recommender Systems
覆盖面广,有思维导图,但没有公式,讲的不详细:
系统离线评估指标

Precision Recall
P和R的分子都是true-positive,P的分母是y_pred的正类数目,R的分母是y_true的正类数目
- P precision 精确率 查准率
- R recall 召回率 查全率
P = T P T P + F P P=\frac{T P}{T P+F P} P=TP+FPTP
R = T P T P + F N R=\frac{T P}{T P+F N} R=TP+FNTP


- TP和FP 表示预测为正类
- TP和FN 表示标签为正类
应用场景
-
推荐系统中比较倾向于高P低R,为了尽可能的不影响用户体验实现更精准推荐。
-
而抓捕逃犯的系统中更需要高的R,误抓也不能漏抓。
MAP MAR
Mean Average Precision (MAP) For Recommender Systems
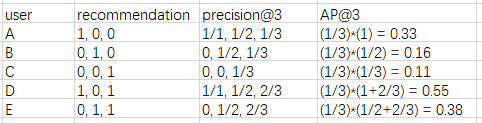
其中m表示用户数目,先计算每个用户的AP,然后再求平均值。
MAP = (0.33+0.16+0.11+0.55+0.38) / 5 = 0.306
覆盖率
覆盖率是指模型能够在测试集上推荐的项目占训练数据的百分比。
个性化
个性化是评估模型是否向不同用户推荐相同项目的方法。用户的推荐列表之间存在差异( 1 − c o n s i n e S i m i l a r i t y 1-consineSimilarity 1−consineSimilarity,余弦距离)。



最后,计算余弦矩阵的上三角的平均值。个性化是1-平均余弦相似度。
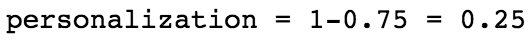
列表内相似性
推荐列表中所有项目的平均余弦相似度。

NDCG
UserCF, ItemFM
五种常见的相似度算法:余弦相似度(cosine_similarity)、jaccard(杰卡德)相似度、编辑距离(Levenshtein)、MinHash、SimHash + 海明距离
要实现协同过滤,需要以下3个步骤:
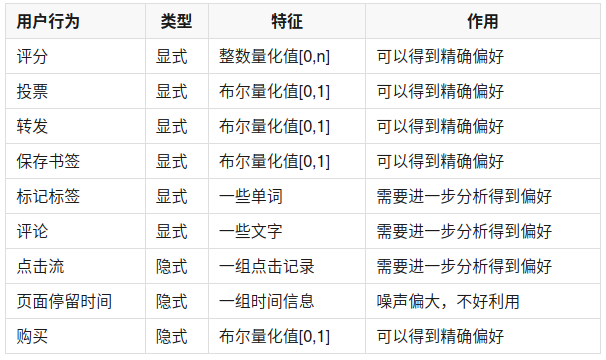
- 收集用户偏好
- 找到相似的用户或物品
- 计算推荐
协同过滤遇到的问题:
- 稀疏性问题——因用户做出评价过少,导致算出的相关系数不准确
- 冷启动问题——因物品获得评价过少,导致无“权”进入推荐列表中
新用户新物品的冷启动策略:
- 给新用户推荐更多平均得分超高的电影;
- 把新电影推荐给喜欢类似电影(如具有相同导演或演员)的人。
后面这种做法需要维护一个物品分类表,这个表既可以是基于物品元信息划分的,也可是通过聚类得到的。
相似度可通过计算欧式距离、皮尔逊相关系数、Cosine相似度、Tanimoto相关系数来衡量:
皮尔逊相关系数(Pearson Correlation Coefficient)
相当于归一化的余弦相似度
p ( x , y ) = ∑ x i y i − n x ˉ y ˉ ( n − 1 ) S x S y = n ∑ x i y i − ∑ x i ∑ y i n ∑ x i 2 − ( ∑ x i ) 2 n ∑ y i 2 − ( ∑ y i ) 2 p(x, y)=\frac{\sum x_{i} y_{i}-n \bar{x} \bar{y}}{(n-1) S_{x} S_{y}}=\frac{n \sum x_{i} y_{i}-\sum x_{i} \sum y_{i}}{\sqrt{n \sum x_{i}^{2}-\left(\sum x_{i}\right)^{2}} \sqrt{n \sum y_{i}^{2}-\left(\sum y_{i}\right)^{2}}} p(x,y)=(n−1)SxSy∑xiyi−nxˉyˉ=n∑xi2−(∑xi)2n∑yi2−(∑yi)2n∑xiyi−∑xi∑yi
Cosine相似度(Cosine Similarity)
T ( x , y ) = x ⋅ y ∥ x ∥ 2 × ∥ y ∥ 2 = ∑ x i y i ∑ x i 2 ∑ y i 2 T(x, y)=\frac{x \cdot y}{\|x\|^{2} \times\|y\|^{2}}=\frac{\sum x_{i} y_{i}}{\sqrt{\sum x_{i}^{2}} \sqrt{\sum y_{i}^{2}}} T(x,y)=∥x∥2×∥y∥2x⋅y=∑xi2∑yi2∑xiyi
Tanimoto系数(Tanimoto Coefficient)
Tanimoto系数由Jaccard系数扩展而来。
T ( x , y ) = x ⋅ y ∥ x ∥ 2 + ∥ y ∥ 2 − x ⋅ y = ∑ x i y i ∑ x i 2 + ∑ y i 2 − ∑ x i y i T(x, y)=\frac{x \cdot y}{\|x\|^{2}+\|y\|^{2}-x \cdot y}=\frac{\sum x_{i} y_{i}}{\sqrt{\sum x_{i}^{2}}+\sqrt{\sum y_{i}^{2}}-\sum x_{i} y_{i}} T(x,y)=∥x∥2+∥y∥2−x⋅yx⋅y=∑xi2+∑yi2−∑xiyi∑xiyi
区别
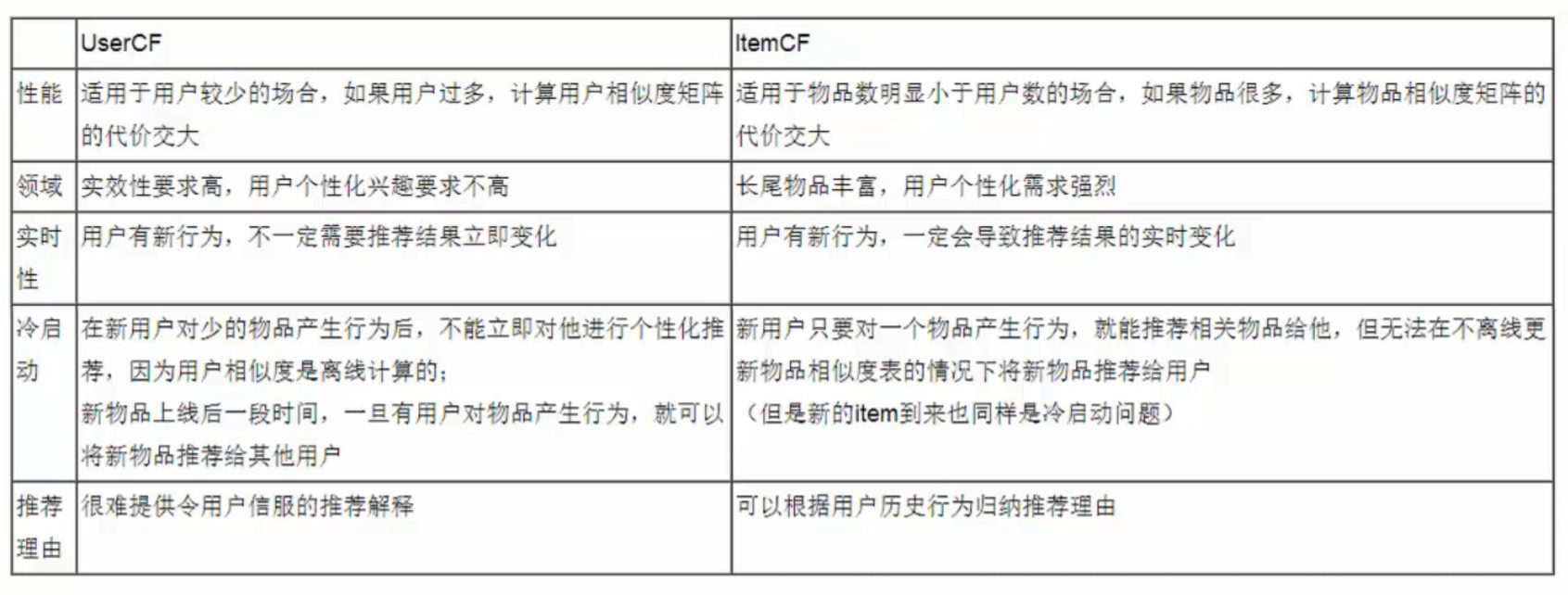
| 区别 | UserCF | ItemCF |
|---|---|---|
| 场景 | 新闻类,短视频类,快消素材网站,社交网站 | 购物网站,技术博客网站 |
| 关注点 | 所在小组中的热门商品,注重社会化 | 注重用户有过行为的历史物品,注重个性化 |
| 多样性 | 系统多样性(覆盖率)高,注重推荐热门物品 | 单用户多样性高,容易推荐长尾物品 |
基于物品(Item-Based,IB) = 基于近邻 = ItemCF
基于内容(Content-Based)与基于近邻:
- 相同点
- 都是在item的基础上做相似度计算
- 不同点
- CB用的是物品本身的特征
- ItemCF用用户对Item的行为来构造Item特征
计算方式
UserCF
- 建立物品到用户的倒排表T
- 根据倒排表计算用户相似度矩阵W
对于物品对应的用户 i j ij ij, W [ i ] [ j ] + = 1 W[i][j]+=1 W[i][j]+=1
惩罚热门物品:
W [ i ] [ j ] + = 1 1 + ∣ N ( i ) ∣ W[i][j]+=\frac{1}{1+|N(i)|} W[i][j]+=1+∣N(i)∣1
ItemCF
- 建立用户到物品倒排表T
- 构建物品相似度矩阵。 w i j w_{ij} wij若不为0,表示有共同的用户对这个物品进行了评分。
LFM
推荐系统SVD
基本公式推导:
rating的预测值
r ^ u i = μ + b u + b i + q j T p u \hat{r}_{u i}=\mu+b_{u}+b_{i}+q_{j}^{T} p_{u} r^ui=μ+bu+bi+qjTpu
带正则化的损失函数
∑ r u i ∈ R train ( r u i − r ^ u i ) 2 + λ ( b i 2 + b u 2 + ∥ q i ∥ 2 + ∥ p u ∥ 2 ) \sum_{r_{u i} \in R_{\text {train }}}\left(r_{u i}-\hat{r}_{u i}\right)^{2}+\lambda\left(b_{i}^{2}+b_{u}^{2}+\left\|q_{i}\right\|^{2}+\left\|p_{u}\right\|^{2}\right) ∑rui∈Rtrain (rui−r^ui)2+λ(bi2+bu2+∥qi∥2+∥pu∥2)
梯度下降
梯度下降的公式很好想明白,因为减去了 r ^ \hat{r} r^,再加上函数求导规则,MSE损失 e 2 e^2 e2的导数就是 2 e ⋅ d e d w 2e\cdot \frac{de}{dw} 2e⋅dwde 。 − b i -b_{i} −bi求导就剩下一个负号了,留下来的就是 − 2 e -2e −2e, p u ⋅ q i p_u\cdot q_i pu⋅qi求导还能留一个(对方)。
e u i = r u i − r ^ u i e_{u i}=r_{u i}-\hat{r}_{u i} eui=rui−r^ui
b u ← b u + γ ( e u i − λ b u ) b i ← b i + γ ( e u i − λ b i ) p u ← p u + γ ( e u i ⋅ q i − λ p u ) q i ← q i + γ ( e u i ⋅ p u − λ q i ) \begin{aligned} b_{u} & \leftarrow b_{u}+\gamma\left(e_{u i}-\lambda b_{u}\right) \\ b_{i} & \leftarrow b_{i}+\gamma\left(e_{u i}-\lambda b_{i}\right) \\ p_{u} & \leftarrow p_{u}+\gamma\left(e_{u i} \cdot q_{i}-\lambda p_{u}\right) \\ q_{i} & \leftarrow q_{i}+\gamma\left(e_{u i} \cdot p_{u}-\lambda q_{i}\right) \end{aligned} bubipuqi←bu+γ(eui−λbu)←bi+γ(eui−λbi)←pu+γ(eui⋅qi−λpu)←qi+γ(eui⋅pu−λqi)
- SVD++
I ( u ) I(u) I(u)为该用户所评价过的所有电影的集合, y j y_j yj为隐藏的“评价了电影 j j j”反映出的个人喜好偏置。
收缩因子取集合大小的根号是一个经验公式,并没有理论依据。
r ^ u i = μ + b u + b i + q i T ( p u + ∣ I u ∣ − 1 2 ∑ j ∈ I u y j ) \hat{r}_{u i}=\mu+b_{u}+b_{i}+q_{i}^{T}\left(p_{u}+\left|I_{u}\right|^{-\frac{1}{2}} \sum_{j \in I_{u}} y_{j}\right) r^ui=μ+bu+bi+qiT(pu+∣Iu∣−21∑j∈Iuyj)
SVD
- 应用
- 数据压缩
- 去除噪声
- A = U Σ V T A=U\Sigma V^T A=UΣVT
- U U T = I U U^{\mathrm{T}}=I UUT=I
- V V T = I V V^{\mathrm{T}}=I VVT=I
- Σ = diag ( σ 1 , σ 2 , ⋯ , σ p ) \Sigma=\operatorname{diag}\left(\sigma_{1}, \sigma_{2}, \cdots, \sigma_{p}\right) Σ=diag(σ1,σ2,⋯,σp)
- σ 1 ⩾ σ 2 ⩾ ⋯ ⩾ σ p ⩾ 0 \sigma_{1} \geqslant \sigma_{2} \geqslant \cdots \geqslant \sigma_{p} \geqslant 0 σ1⩾σ2⩾⋯⩾σp⩾0
- p = min ( m , n ) p=\min (m, n) p=min(m,n)
- 求解步骤
- 确定 V V V 和 Σ \Sigma Σ
- V T ( A T A ) V = Λ V^{\mathrm{T}}\left(A^{\mathrm{T}} A\right) V=\Lambda VT(ATA)V=Λ
- 计算 Λ \Lambda Λ特征值的平方根
- σ j = λ j , j = 1 , 2 , ⋯ , n \sigma_{j}=\sqrt{\lambda_{j}}, \quad j=1,2, \cdots, n σj=λj,j=1,2,⋯,n
- Σ ₁ = d i a g ( σ ₁ , σ ₂ , ⋯ , σ r ) \Sigma₁=diag(\sigma₁, \sigma₂, \cdots,\sigma_r) Σ₁=diag(σ₁,σ₂,⋯,σr)
- Σ = [ Σ 1 0 0 0 ] \Sigma=\left[\begin{array}{ll}\Sigma_{1} & 0 \\ 0 & 0\end{array}\right] Σ=[Σ1000]
- V = [ V ₁ V ₂ ] V=[V₁ V₂] V=[V₁V₂], 其中 V ₁ V₁ V₁为 r r r列
- 确定 U U U
- u j = 1 σ j A v j , j = 1 , 2 , ⋯ , r u_{j}=\frac{1}{\sigma_{j}} A v_{j}, \quad j=1,2, \cdots, r uj=σj1Avj,j=1,2,⋯,r
- U 1 = [ u 1 u 2 ⋯ u r ] U_{1}=\left[\begin{array}{llll}u_{1} & u_{2} & \cdots & u_{r}\end{array}\right] U1=[u1u2⋯ur]
- A V 1 = U 1 Σ 1 A V_{1}=U_{1} \Sigma_{1} AV1=U1Σ1
- 确定 V V V 和 Σ \Sigma Σ
- 紧凑奇异值分解
- 无损压缩
- 截断奇异值分解
- 有损压缩
PCA
没时间看统计学习方法了,看了这个野博客:
机器学习数学基础:从奇异值分解 SVD 看 PCA 的主成分
X X X减去每列均值做零中心化,得到协方差矩阵(对称矩阵,半正定矩阵(所有特征值>=0)),然后做特征分解,得到特征向量矩阵 Q Q Q
C = X ⊤ X m − 1 = Q Λ Q − 1 \begin{aligned} \mathbf{C} &=\frac{\mathbf{X}^{\top} \mathbf{X}}{m-1} \\ &=\mathbf{Q} \mathbf{\Lambda} \mathbf{Q}^{-1} \end{aligned} C=m−1X⊤X=QΛQ−1
式中 m m m 表示 m m m 个样本,上面除以 m − 1 m-1 m−1 是为了无偏估计。
Q Q Q的前K个向量就是我们要找的主成分PC。将数据投影到PC上去,即 Y = X Q Y=XQ Y=XQ,投影后的数据的协方差:
C Y = Y ⊤ Y m − 1 = Q ⊤ X ⊤ X Q m − 1 = Q ⊤ Q Λ Q − 1 Q = Λ \begin{aligned} \mathbf{C}_{\mathbf{Y}} &=\frac{\mathbf{Y}^{\top} \mathbf{Y}}{m-1} \\ &=\frac{\mathbf{Q}^{\top} \mathbf{X}^{\top} \mathbf{X} \mathbf{Q}}{m-1} \\ &=\mathbf{Q}^{\top} \mathbf{Q} \mathbf{\Lambda} \mathbf{Q}^{-1} \mathbf{Q} \\ &=\mathbf{\Lambda} \end{aligned} CY=m−1Y⊤Y=m−1Q⊤X⊤XQ=Q⊤QΛQ−1Q=Λ
以上做法就是常见的对协方差矩阵做特征分解的操作。工业上(详见sklearn代码)的操作是更一般的对数据矩阵做SVD。
众所周知,SVD张这样:
X = U Σ V T X=U\Sigma V^T X=UΣVT
C = X ⊤ X m − 1 = ( V Σ U ⊤ ) ( U Σ V ⊤ ) m − 1 = V Σ 2 V ⊤ m − 1 = V Σ 2 V − 1 m − 1 \begin{aligned} \mathbf{C} &=\frac{\mathbf{X}^{\top} \mathbf{X}}{m-1} \\ &=\frac{\left(\mathbf{V} \mathbf{\Sigma} \mathbf{U}^{\top}\right)\left(\mathbf{U} \mathbf{\Sigma} \mathbf{V}^{\top}\right)}{m-1} \\ &=\frac{\mathbf{V} \mathbf{\Sigma}^{2} \mathbf{V}^{\top}}{m-1} \\ &=\frac{\mathbf{V} \mathbf{\Sigma}^{2} \mathbf{V}^{-1}}{m-1} \end{aligned} C=m−1X⊤X=m−1(VΣU⊤)(UΣV⊤)=m−1VΣ2V⊤=m−1VΣ2V−1
然后和比一下:
C = X ⊤ X m − 1 = Q Λ Q − 1 \begin{aligned} \mathbf{C} &=\frac{\mathbf{X}^{\top} \mathbf{X}}{m-1} \\ &=\mathbf{Q} \mathbf{\Lambda} \mathbf{Q}^{-1} \end{aligned} C=m−1X⊤X=QΛQ−1
就会发现,我们想要的主成分就是
Q = V m − 1 Q=\frac{V}{\sqrt{m-1}} Q=m−1V
同理:
Λ = Σ 2 m − 1 \mathbf{\Lambda}=\frac{\boldsymbol{\Sigma}^{2}}{m-1} Λ=m−1Σ2
笔记:
- 协方差矩阵求解公式
- Σ = cov ( x , x ) = E [ ( x − μ ) ( x − μ ) T ] \Sigma=\operatorname{cov}(\boldsymbol{x}, \boldsymbol{x})=E\left[(\boldsymbol{x}-\boldsymbol{\mu})(\boldsymbol{x}-\boldsymbol{\mu})^{\mathrm{T}}\right] Σ=cov(x,x)=E[(x−μ)(x−μ)T]
- 总体PCA
- m m m维向量 x x x到 m m m维向量 y y y的线性变换
- y i = α i T x = α 1 i x 1 + α 2 i x 2 + ⋯ + α m i x m y_{i}=\alpha_{i}^{\mathrm{T}} \boldsymbol{x}=\alpha_{1 i} x_{1}+\alpha_{2 i} x_{2}+\cdots+\alpha_{m i} x_{m} yi=αiTx=α1ix1+α2ix2+⋯+αmixm
- 满足
- A A A是标准正交基
- c o v ( y i , y j ) = 0 ( i ≠ j ) cov(y_i,y_j)=0(i\neq j) cov(yi,yj)=0(i=j)
- y ₁ y₁ y₁方差最大,为第一主成分,以此类推
- 求解
- 第一主成分最大 var ( α 1 T x ) = α 1 T Σ α 1 \operatorname{var}\left(\alpha_{1}^{\mathrm{T}} \boldsymbol{x}\right)=\alpha_{1}^{\mathrm{T}} \Sigma \alpha_{1} var(α1Tx)=α1TΣα1
- 问题定义
- max α 1 α 1 T Σ α 1 s.t. α 1 T α 1 = 1 \begin{array}{ll}\max _{\alpha_{1}} & \alpha_{1}^{\mathrm{T}} \Sigma \alpha_{1} \\ \text { s.t. } & \alpha_{1}^{\mathrm{T}} \alpha_{1}=1\end{array} maxα1 s.t. α1TΣα1α1Tα1=1
- 定义拉格函数
- α 1 T Σ α 1 − λ ( α 1 T α 1 − 1 ) \alpha_{1}^{\mathrm{T}} \Sigma \alpha_{1}-\lambda\left(\alpha_{1}^{\mathrm{T}} \alpha_{1}-1\right) α1TΣα1−λ(α1Tα1−1)
- 对 a ₁ a₁ a₁求导令其为0, 得到
- Σ α 1 − λ α 1 = 0 \Sigma \alpha_{1}-\lambda \alpha_{1}=0 Σα1−λα1=0
- 其实就是特征值和特征向量
- 结论
- x x x的第 k k k主成分是协方差矩阵 Σ \Sigma Σ第 k k k特征值
- m m m维向量 x x x到 m m m维向量 y y y的线性变换
- 样本PCA
- 对样本数据规范化
- x i j ∗ = x i j − x ˉ i s i i , i = 1 , 2 , ⋯ , m ; j = 1 , 2 , ⋯ , n x_{i j}^{*}=\frac{x_{i j}-\bar{x}_{i}}{\sqrt{s_{i i}}}, \quad i=1,2, \cdots, m ; \quad j=1,2, \cdots, n xij∗=siixij−xˉi,i=1,2,⋯,m;j=1,2,⋯,n
- x ˉ i = 1 n ∑ j = 1 n x i j , i = 1 , 2 , ⋯ , m \bar{x}_{i}=\frac{1}{n} \sum_{j=1}^{n} x_{i j}, \quad i=1,2, \cdots, m xˉi=n1∑j=1nxij,i=1,2,⋯,m
- s i i = 1 n − 1 ∑ j = 1 n ( x i j − x ˉ i ) 2 , i = 1 , 2 , ⋯ , m s_{i i}=\frac{1}{n-1} \sum_{j=1}^{n}\left(x_{i j}-\bar{x}_{i}\right)^{2}, \quad i=1,2, \cdots, m sii=n−11∑j=1n(xij−xˉi)2,i=1,2,⋯,m
- 样本协方差矩阵 S S S就是样本相关矩阵 R R R
- R = 1 n − 1 X X T R=\frac{1}{n-1} X X^{\mathrm{T}} R=n−11XXT
- 传统方法: 对协方差矩阵做特征值分解
- 求解 R R R的 k k k个特征值
- ∣ R − λ I ∣ = 0 |R-\lambda I|=0 ∣R−λI∣=0
- 第k主成分的方差贡献率
- η k = λ k ∑ i = 1 m λ i \eta_{k}=\frac{\lambda_{k}}{\sum_{i=1}^{m} \lambda_{i}} ηk=∑i=1mλiλk
- 求方差贡献率达到预订值的主成分个数 k k k
- 求前 k k k个特征值对应的单位特征向量
- a i = ( a 1 i , a 2 i , ⋯ , a m i ) T , i = 1 , 2 , ⋯ , k a_{i}=\left(a_{1 i}, a_{2 i}, \cdots, a_{m i}\right)^{\mathrm{T}}, \quad i=1,2, \cdots, k ai=(a1i,a2i,⋯,ami)T,i=1,2,⋯,k
- 求 k k k个样本主成分
- y i = a i T x , i = 1 , 2 , ⋯ , k y_{i}=a_{i}^{\mathrm{T}} \boldsymbol{x}, \quad i=1,2, \cdots, k yi=aiTx,i=1,2,⋯,k
- 常用方法: 数据矩阵的奇异值分解
- 野博客
- https://mp.weixin.qq.com/s/kUlulnusW8zXfq-cXdGMWg
- 奇异值分解的本质是求协方差矩阵 S S S的特征值和特征向量
- X ′ = 1 n − 1 X T X^{\prime}=\frac{1}{\sqrt{n-1}} X^{\mathrm{T}} X′=n−11XT
- X ′ T X ′ = ( 1 n − 1 X T ) T ( 1 n − 1 X T ) = 1 n − 1 X X T \begin{aligned} X^{\prime \mathrm{T}} X^{\prime} &=\left(\frac{1}{\sqrt{n-1}} X^{\mathrm{T}}\right)^{\mathrm{T}}\left(\frac{1}{\sqrt{n-1}} X^{\mathrm{T}}\right) \\ &=\frac{1}{n-1} X X^{\mathrm{T}} \end{aligned} X′TX′=(n−11XT)T(n−11XT)=n−11XXT
- S X = X ′ T X ′ S_{X}=X^{\prime \mathrm{T}} X^{\prime} SX=X′TX′
- 对 X ′ X^\prime X′做奇异值分解, V V V的列向量就是 X ′ T X ′ X^{\prime \mathrm{T}} X^{\prime} X′TX′( S S S)的单位特征向量
- 野博客
- 对样本数据规范化
- PCA的先导知识是[[SVD]]
白化
常用来进行白化的操作有两种方式,一种是PCA whiten,另外一种是ZCA whiten。
More importantly, understanding PCA will enable us to later implement whitening, which is an important pre-processing step for many algorithms.
There is a closely related preprocessing step called whitening (or, in some other literatures, sphering) which is needed for some algorithms.
- (i) the features are less correlated with each other, and
- (ii) the features all have the same variance.
其实就是让协方差矩阵变成单位矩阵
有PCA Whitening和ZCA Whitening
有空看下这个,没时间看了