排序（2）交换排序和选择排序

1. 交换排序

基本思路：两个记录反序时进行交换。
常见的交换排序方法：（1）冒泡排序（2）快速排序。

冒泡排序

基本思想：从后往前（或从前往后）两两比较相邻元素的值，若为逆序，则交换它们，直到序列比较完。在下一趟冒泡时，上一趟确定的最小（或最大）元素不再参与比较，每次冒泡都将无序区中的最小（或最大）元素放在其最终位置。
一旦某趟冒泡过程不进行记录交换，说明已经排好序了，就可以结束本算法。最多进行n-1趟冒泡。
算法分析：最好的情况（关键字在记录中正序），只需要一趟冒泡，比较n-1次，移动0次；最坏的情况（反序），需进行n-1趟冒泡，比较$1+...+n-1=n(n-1)/2$次，移动$3(1+...+n-1)=3n(n-1)/2$。所以冒泡排序最好的时间复杂度为$O(n)$，最坏和平均都是$O(n^2)$。
空间效率：仅使用了常数个辅助单元，空间复杂度为$O(1)$。
稳定性：关键字相等是不进行交换，是一种稳定的排序算法。

void BubbleSort(RecType A[], int n){
    
    //冒泡排序
    int i, j;
    RecType tmp;
    for (i=1; i<n; i++){
    
    //进行n-1趟排序
        int flag = 0;//判断本趟是否出现记录交换
        for (j=0; j<n-i; j++){
    
    
            if (A[j].key > A[j+1].key){
    
    //交换
                tmp = A[j];
                A[j] = A[j+1];
                A[j+1] = tmp;
                flag = 1;
            }
        }
        if (flag == 0)//本趟不出现记录交换，已经排好序了
            break;
    }
}

快速排序

基本思想：每次将表的第一个元素放在适当位置（归位），将表一分为二，对子表按递归方式继续这种划分，直至划分的子表的长度为0或1（递归出口）。
空间效率：快速排序是递归的，需要借助一个递归工作栈来保存每层递归调用的必要信息，其容量应与递归调用的最大深度一致。最好情况为$O(lo{g}_{2}n)$，最坏情况为$O(n)$。
时间效率：快速排序的运行时间与划分是否对称有关。最好情况，每次划分都对称，为$O(nlo{g}_{2}n)$，最坏情况，每次划分都是一个区间包含0个元素而另一个区间包含n-1个元素，为$O(n^2)$。快速排序平均情况下的运行时间接近于最好的情况，是所有内部排序算法中平均性能最优的排序算法。
稳定性：是不稳定的排序算法。若右端区间有两个关键字相同的记录，且均小于基准值的记录，则交换到左区间后，相对位置发生变化。

void QuickSort(RecType A[], int low, int high){
    
    //快速排序
    int i = low, j = high;
    RecType tmp;
    if (low<high){
    
    //至少两个元素
        tmp = A[low];//基准
        while (i!=j){
    
    
            while (i<j && A[j].key>=tmp.key) j--;//找小于基准的元素
            A[i] = A[j];
            while (i<j && A[i].key<=tmp.key) i++;//找大于基准的元素
            A[j] = A[i];
        }
        A[i] = tmp;
        QuickSort(A,low,i-1);//对左区间进行递归排序
        QuickSort(A,i+1,high);//右区间递归排序
    }
    //少于一个元素，为递归出口
}

int Partition(vector<int>& arr, int start, int end){
    
    
    int i = start, j = end;
    int tmp = arr[i];
    while (i < j){
    
    
        while (i < j && arr[j] >= tmp) j--;
        arr[i] = arr[j];
        while (i < j && arr[i] <= tmp) i++;
        arr[j] = arr[i];
    }
    arr[i] = tmp;
    return i;
}
void QuickSort(vector<int>& arr, int left, int right){
    
    
    if (left < right){
    
    
        int idx = Partition(arr,left,right);
        QuickSort(arr,left,idx-1);
        QuickSort(arr,idx+1,right);
    }
}

2.选择排序

第i趟从L[i,…,n]选择关键字最小的元素，放在L(i)处。

简单选择排序

基本思想：假设排序表为L[1,2,…,n]，第i趟排序即从L[i,…,n]中选择关键字最小的元素与L(i)交换，每一趟排序可以确定一个元素的最终位置，这样经过n-1趟排序就可以使整个表有序。
空间效率：仅使用常量个辅助单元，故空间效率为$O(n)$.
时间效率：移动记录的次数，最好情况（正序）为0，最坏情况（反序）为$3(n-1)$。关键字的比较次数与序列的初始状态无关，始终为$1+...+(n-1)=n(n-1)/2$次，时间复杂度始终为$O(n^2)$。
稳定性：是不稳定的方法。在第i趟找到最小元素后，和第i个元素交换，可能导致第i个元素与其含有相同关键字元素的相对位置发生改变。

void SelectSort(RecType A[], int n){
    
    //简单选择排序
    int i, j, min; RecType tmp;
    for (i=0; i<n-1; i++){
    
    //共进行n-1趟排序
        min = i;
        for (j=i+1; j<n; j++){
    
    
            if (A[j].key<A[min].key)
                min = j;//更新最小值的位置
        }
        if (min != i){
    
    
            tmp = A[i]; A[i] = A[min]; A[min] = tmp;//交换
        }
    }
}

堆排序

堆的定义：n个关键字序列$L[1...n]$称为堆，当且仅当该序列满足：
（1）$L(i)>=L(2i)且L(i)>=L(2i+1)$或者
（2）$L(i)<=L(2i)且L(i)<=L(2i+1) $, $(1<=i<=\lfloor n/2\rfloor )$
满足（1）的称为大根堆，满足（2）的称为小根堆。
可以将该关键字序列视为一棵完全二叉树，大根堆的最大元素存放在根节点，且任一非根节点的值小于等于其双亲节点值。小根堆正好相反。
堆排序的思路：由关键字序列创建初始堆。由堆自身的特点，堆顶元素就是最大值。输出堆顶元素后，通常将堆底元素送入堆顶，此时根节点不满足大根堆的性质，堆被破坏，将堆顶元素向下调整使其继续保持大根堆的性质，再输出堆顶元素。如此充分，直到堆中仅剩一个元素为止。
关键问题：（1）如何将无序序列构建成初始堆；（2）输出堆顶元素后，如何将剩余元素调整成新的堆？
算法设计：构建初始堆：对以第$\lfloor n/2\rfloor$个节点为根的子树进行筛选（对于大根堆，若根节点的关键字小于左右孩子中关键字的较大者，则交换之），使该子树成堆。之后向前依次对各分支节点（$\lfloor n/2\rfloor -11$）为根的子树进行筛选，直到根节点。

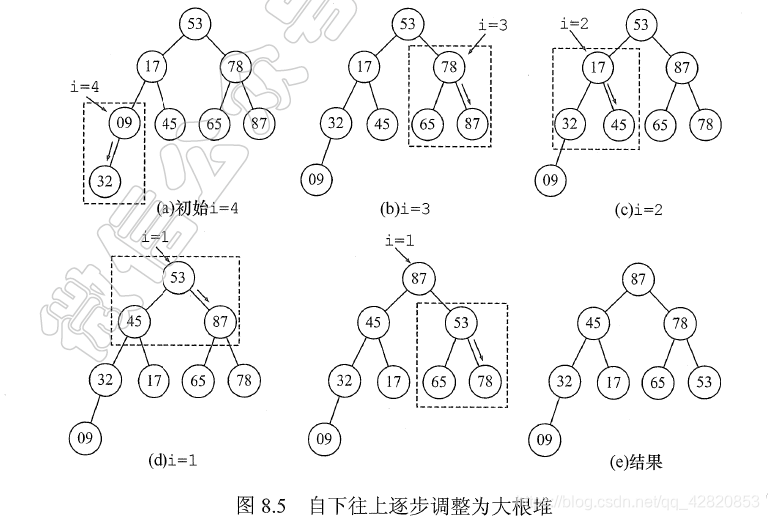
输出堆顶元素后，将堆的最后一个元素与堆顶元素交换，此时堆的性质被破坏，需要向下进行筛选。

空间效率：仅使用了常数个辅助单元，空间复杂度为$O(1)$。
时间效率：建堆时间为$O(n)$，在最好、最坏和平均情况下，堆排序的时间复杂度为$O(nlo{g}_{2}n)$.
稳定性：是不稳定的算法。

void Sift(RecType A[], int low, int high){
    
    //对以low为根节点子树筛选
    int i=low, j=2*i;
    RecType tmp = A[i];
    while (j<=high){
    
    
        if (j<high && A[j].key<A[j+1].key) j++;//j指向大孩子
        if (tmp.key<A[j].key){
    
    
            A[i] = A[j];//将A[j]调整到双亲节点的位置上
            i = j;//修改i和j的值，以便继续向下筛选
            j = 2*i;
        }
        else break;//双亲大，不用调整
    }
    A[i] = tmp;
}
void HeapSort(RecType A[], int n){
    
    //堆排序
    int i;
    RecType tmp;
    for (i=n/2; i>=1; i--)//循环建立初始堆
        Sift(A,i,n);
    for (i=n; i>=2; i--){
    
    //进行n-1次循环，完成堆排序
        tmp = A[1];
        A[1] = A[i];
        A[i] = tmp;
        Sift(A,1,i-1);
    }
}

void adjust(vector<int> &nums, int i, int n){
    
    
    int j = 2 * i + 1;
    while (j < n){
    
    
        if (j < n - 1 && nums[j] < nums[j+1])
            j++;//j指向两个子节点中较大的
        if (nums[i] < nums[j]){
    
    
            int tmp = nums[i];
            nums[i] = nums[j];
            nums[j] = tmp;
            i = j;//继续向下调整
            j = 2*i + 1;
        }
        else
            break;
    }
}
void HeapSort(vector<int> &nums){
    
    
    int n = nums.size();
    for (int i = n/2 - 1; i >= 0; i--)//创建初始堆
        adjust(nums,i,n);
    for (int j = n-1; j >= 1; j--){
    
    //进行n-1次循环，完成堆排序
        int tmp = nums[0];
        nums[0] = nums[j];
        nums[j] = tmp;
        adjust(nums,0,j);
    }
}

int main(){
    
    
    vector<int> nums{
    
    10,3,2,6,5,4,9,7,8};
    HeapSort(nums);
    for (int i =0; i < nums.size(); i++)
        cout << nums[i] << endl;
    return 0;
}