期望题 hdu 6747 Rotate 2020百度之星初赛一 T5 题解

补题传送门：hdu 6747
前6题题解
感谢[csdn tomjobs的]这篇博客与[csdn dongdongdong122]的这篇博客
本博客对上述博客中的思路重新进行了解释并融合了一些自己的想法

Problem Description
我们有一个圈，从内到外一共被分成了 n 个环，中间是空的。

我们把从外到内第 i 层环平分成 a[i] 份，其中 a[i] 是偶数，我们把这 a[i] 份黑白染色，第奇数个染成黑色，第偶数个染成白色。

现在我们旋转每一层，每一层都会等概率随机到一个中止位置。

问黑色的联通块数目的期望。两块黑色的区域有交点即算联通。层之间的旋转是相互独立的。
Input
第一行一个正整数
test(1≤test≤10) 表示数据组数。

对于每组数据，第一行一个正整数 n(1≤n≤10)。

接下来一行 n 个正整数 ai，a[i] 为偶数，另外保证 a 序列不降。

Output
对于每组数据，一行一个数表示答案，由于答案 A/B 中的 AB 可能很大，请输出 A/Bmod109+7，假设 A/B
为最简分数，A/Bmod109+7=A∗B−1mod109+7，B−1 为满足 B−1∗Bmod109+7=1 的整数。

1. 基础概念

1.1 联通块

首先我们需要知道什么叫一个联通块？这里的联通块与图论中的是一样的。
比如这样的一个图求@构成的联通块，一眼就能看出来是三个。

@........@..
.@@@.....@@@
....@@...@@.
.........@@.
.........@..
..@......@..
.@.@.....@@.
@.@.@.....@.
.@.@......@.
..@.......@.

下面这个两层的环的联通块数就是两块
在这里插入图片描述

1.2 临界情况

本题中的“每一层都会等概率随机到一个中止位置”，在概率论中属于几何概型，
因为临界区间的长度是0，所以到临界位置的概率也是0，所以算期望时可以不用考虑。

2. 寻找相邻层块的连接或包裹关系

我们得固定一个环来分析，固定哪个都行。接下来我们分别进行介绍。

2.1固定内环旋转外环

2.1.1 被外层黑块连接的黑块数

现在我们把内层分成12块外层分成4块。
那么外层一块的大小相当于内层3块
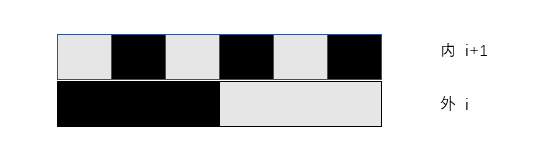
在这里插入图片描述
我们关注下面的那个黑块，可以发现一个外层的块能连接到的块是4=3+1
上图显示的是临界情况：完整的三块和边界的一块
再往右一点呢？就是完整的两块和两边两个半块
连接只要能碰到就行，所以两个半块可以当作两块

推广到一般的情况呢？
外层（i）一块能连接的内层（i+1）块数就是： $\frac{a[i+1]}{a[i]}+1$
而内层块中黑白是均匀分布的所以外层一个块能连接到的黑块是 $\frac{\frac{a[i+1]} {a[i]}+1}{2}$

可以移动一下上图中的块，会发现外环一个块总能连接内环（（3+1）/2 = 2）个黑块。

2.1.2 被外层白块包裹的黑块数

2.1.2.1 取补集法

对于内层任意一个黑块只有可能有两个状态：被外层黑块连接，被外层白块包裹
所以内层总黑块数 $\frac{a[i+1]}{2}$ 减去被外层黑块连接的： $\frac{a[i]}{2}*\frac{\frac{a[i+1]}{a[i]}+1}{2}=\frac{a[i+1]+a[i]}{4}$ 便得到了第i+1层被外层白块包裹的黑块数： $\frac{a[i+1]-a[i]}{4}$

2.1.2.2 正面分析法

前面的例子中一个外层块能“连接”4个内层块，那能“包裹”几个呢？

包裹要求内层的块要完整，所以临界状态是3个但是第三个会算到与黑块连接，所以是2个，其他情况（如上图）也是2个。
推广到一般：
外层（i）一块能连接的内层（i+1）块数就是： $\frac{a[i+1]}{a[i]}-1$
黑白还是均匀分布所以平均分配。
第i+1层被外层白块包裹的黑块数： $\frac{\frac{a[i]}{2}*(\frac{a[i+1]}{a[i]}-1)}{2}=\frac{a[i+1]-a[i]}{4}$

2.2 固定外环旋转内环

2.2.1 被外层白块包裹的黑块数

内层总共可移动的范围是左侧橙线到右侧蓝线
只有在左侧橙线到右侧橙线之间移动，内层一个块才被外层完全包裹，
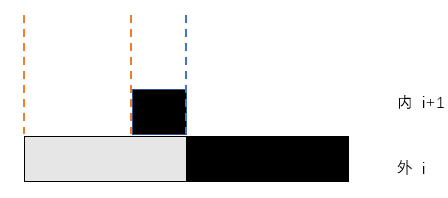
在这里插入图片描述

所以被包裹的概率是2/3，也就是说2/3的黑块被外层块包裹。
外层块的黑白块也平均分配所以有2/（3*2）的黑块被白块包裹。
乘上内层黑块数便得到了被包裹的黑块数
推广到一般：
被包裹的概率是: $1-\frac{a[i]}{a[i+1]}$
第i+1层被外层白块包裹的黑块数： $\frac{\frac{a[i+1]}{2}*(1-\frac{a[i]}{a[i+1]})}{2}=\frac{a[i+1]-a[i]}{4}$

3. 求联通块数

3.1 看作森林，点数减边数

3.1.1 为何强调 $a_i$ 单调？

在这里插入图片描述
我们来分析一波这个官方题解。
这里的 $a_i$ 递减改成 $a_i$ 递增更合适，但知道单调就行了。
强调 $a_i$ 单调，并因此联通块可以构成森林。
不妨考虑一下如果 $a_i$ 不单调会是什么样子
将黑块看作节点，如果与相邻层有连接则连接两个节点。
现给出一个 $a_i$ 的序列：6 2 6
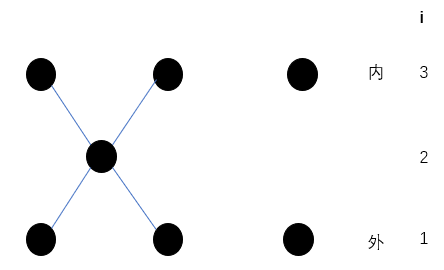
在这里插入图片描述

这里出现了内层黑块连接两个外层黑块的情况，也就出现了一个儿子有多个父亲的情况，不符合树的定义。

3.1.2 为何是点数减边数？

树的性质：点数-边数=1
一个结点也可以看作一颗树，所以对于森林而言，点数减边数便能得到森林中树的数量。
而一棵树便对应着一个联通块。

3.1.3 具体如何算？

在第二节中我们已经知道相邻层的连接情况了，第i+1层有： $\frac{a[i+1]+a[i]}{4}$ 个黑块被第i层黑块连接，这就是这两层间的边数，i+1层点数减边数，得i+1层对结果的贡献： $\frac{a[i+1]-a[i]}{4}$ ，最外层只有点没有边所以为 $\frac{a[1]}{2}$ .
累加：
$\frac{a[n]-a[n-1]}{4}+\frac{a[n-1]-a[n-2]}{4}+...+\frac{a[2]-a[1]}{4}+\frac{a[1]}{2}=\frac{a[n]+a[1]}{4}$

3.2 分析被白块包裹的黑块

如果一个黑块被连接，那么它是联通块的中间节点，向外还有其余的部分。那么如何表示一个联通图的结束呢？
没错，被白块包裹的黑块，这个白块中止了这个图再向外延伸，同时这个黑块也是这棵树的顶点，也就是数的根。（这里我们还是得承认这个联通块是一个树形结构）
也就是说除了点数减边数等于一能标识一棵树，树根也可以标识一棵树。
而第i+1层被外层白块包裹的黑块数： $\frac{a[i+1]-a[i]}{4}$
与我们上一种方法分析的i+1层的贡献一致。
我们不妨再想一下两个什么一致？
我们发现除了最外层，被连接的黑块对结果是没有贡献的！因为这个黑块都是树的中间节点与叶子节点，而他们的多少跟我们有几棵树是没有关系的。
那最外层为何特殊？
最外层外相当于有一个整个一个环那么大的白块，把最外层的黑块包裹。
或者我们也不必强行拉到我们的黑白块理论，这些黑块外啥也没有了，自然这棵树就中止不再延伸了。

4. 求逆元

逆元属于基础知识了。
其他博客的代码大多是用的快速幂求逆元，所用的理论是：费马小定理，但要求模为素数。本题中的1e9+7正好为素数。一般这种题也只能给个素数，不然如果不互质就没法算了。
为什么不互质就没法算了？
主要和逆元的性质有关，理论我也不是很懂，这里就不解释了。
但求逆元还有一个更加普世的方法：扩展欧几里得算法。它不要求模数是素数，只要互质就行。
这里推荐几个关于扩展欧几里得求逆元文章。

前述解释较好：简书 ffffffffffffly
公式推理易懂：csdn zy010101

扩展阅读

变量比较习惯用a，b所以代码我看的这篇: csdn _Warning_
取模运算规则博客园 qmyc1999

值得注意的是，分数也可以取模
比如（5/2 ）mod 3 。2在模3意义下的逆元是2，5*2=10 模上3就是1.所以5/2在模3意义下的就是1.
我们可以验证一下这个结果的合理性：
2*（5/2 ）mod 3=5 mod 3=2
2*1 mod 3 = 2
代码

#include<iostream>
using namespace std;
typedef long long ll;
const int n_max=10;
int exgcd(int a,int b,int &x,int &y)
{
    
    
    if(b==0)
    {
    
    
        x=1;
        y=0;
        return a;
    }
    int r=exgcd(b,a%b,x,y);
    int temp=y;
    y=x-(a/b)*y;
    x=temp;
    return r;
}
int inverse(int a,int p)
{
    
    
    int x,y;
    int gcd=exgcd(a,p,x,y);
    return (x+p)%p; //保证结果为正数
}
int test;
int a[n_max+1];
int n;
int mod= 1e9+7;
int main()
{
    
    
    cin>>test;
    for(int k=0; k<test; k++)
    {
    
    
        cin>>n;
        for(int i=1;i<=n;i++)
        {
    
    
            scanf("%d",&a[i]);   
        }
        cout<<(ll)(a[n]+a[1])*inverse(4,mod)%mod<<endl;
    }
}

5. 反思为什么之前不会这道题

不了解联通块的概念，且不知道分数取模可能得到奇怪的数，看到示例给个大数就怀疑是不是把联通子图也得算上，然后就搞不清楚示例了，很久之后才知道原来和图论里的联通图是一样的。之后问题的本质也没有很快地搞清楚。继续加油吧