树状数组的另一种讲解

树状数组的讲解

最近为了给女票讲好树状数组，就再次接触了这个让人比较头疼的数据结构，之前看了网上其它的树状数组的教程，感觉看完能够会用，但并不是能够比较好的理解。因为先接触的线段树，而且线段树从操作还是意义来说都会更加直观易懂一些，所以我个人从线段树的角度出发，找到了一个自己比较容易理解的方向来描述了树状数组。

1.树状数组的元素

首先，我们先考虑这么一棵满二叉树形式的表示区间和的线段树，每个节点表示的范围我已经标了出来：
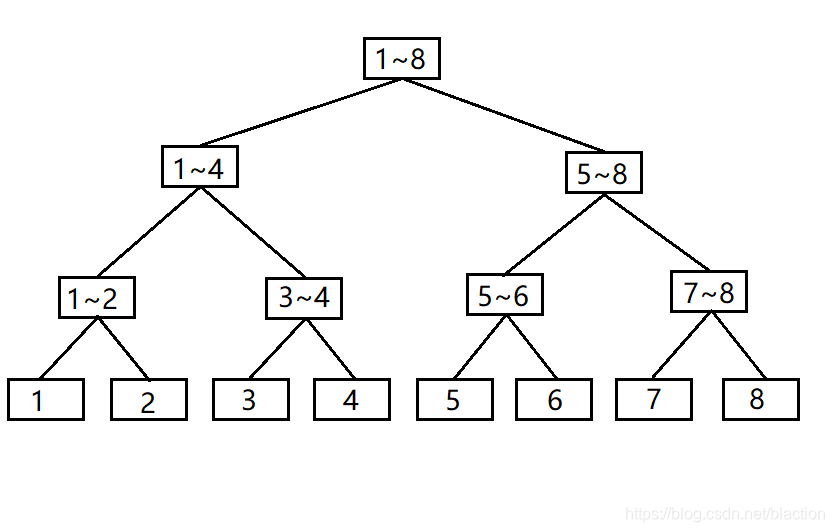
在这里插入图片描述
相信对于上面这棵满二叉树，我们在了解线段树之后并不陌生，而且线段树对应的相关操作更直观易懂，但是花费的空间相对更多，下面我们先为了有效的节约空间，我们将这棵二叉树做如下调整。

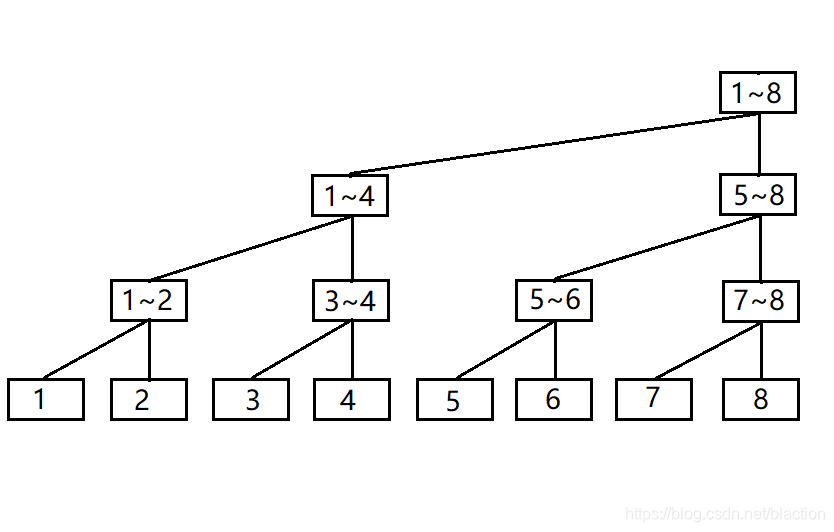
简言之就是把每个父节点放置于每个右儿子的正上方，这样如果我们有 n 个数（此样例中是8个数），那么我们从左往右就一共会有 n 个竖列（此样例中是8个），那么好，我们为了有效的节省空间，不存储多余的信息，把冗余清除掉，每一竖列只留最上面的一个节点，那么就是如下图所示。
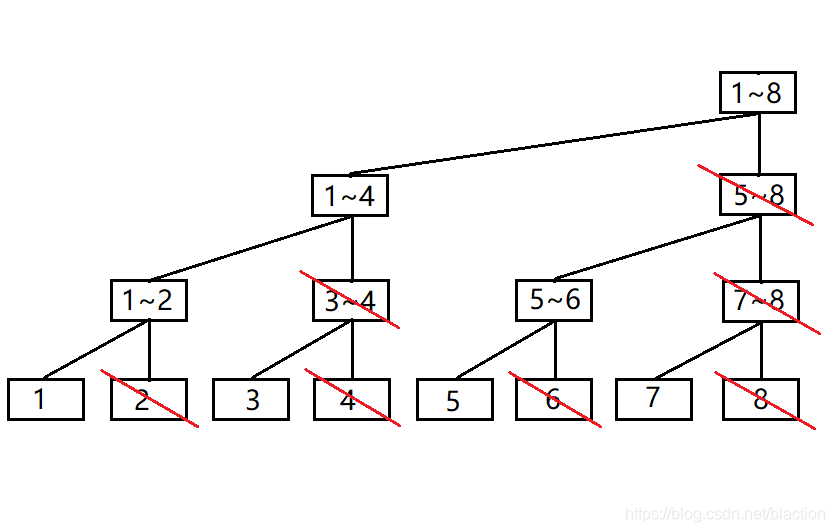
在这里插入图片描述
那么这个时候，我们就可以用一个长度为 n （此样例为8）的数组来记录我们需要记录的信息，这就是我们的树状数组，每一个元素表示的区间和的区间我在下图这张新图中用红框表示了出来。（紫色是数组下标）
在这里插入图片描述
那么对于这么一个长度为 n（此样例为8）的数组，我们怎么求出来它所在的位置 $i$ 的元素（即下标为 $i$ 的元素）代表的区间和的区间是多少呢？可能有的小伙伴会抢答，设这个数组元素下标是 $i$ ， $i$ 对应的二进制最后一个 $1$ 右面有 $x$ 个0，那么范围就是 $i-2^{x}+1,i]$ ，那么你有没有考虑过为什么是这个样子呢？

因为我们的区间和是向上传递的，所以对于每个位置 $i$ ，我们一定会存在一个以 $i$ 为最底层最右面的叶子节点的满二叉树，而这个满二叉树的叶子节点的个数，就是我们位置 $i$ 所对应区间和的区间大小。比如下图中：
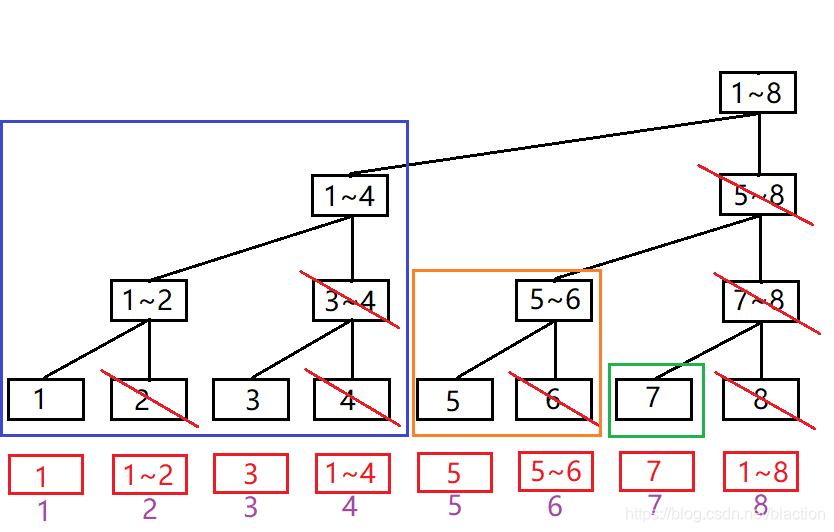
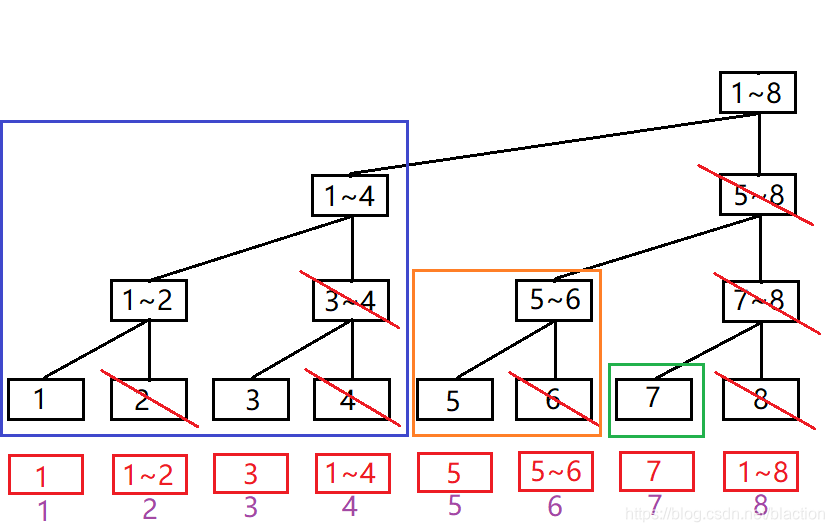
在这里插入图片描述

$i = 4$ 对应的满二叉树我用蓝框圈了出来，对应的满二叉树有4个叶子节点，所以该位置表示的区间和对应区间就是 $[1, 4]$ ；
$i = 6$ 对应的满二叉树我用橙框圈了出来，对应的满二叉树有2个叶子节点，所以该位置表示的区间和对应区间就是 $[5, 6]$ ；
$i = 7$ 对应的满二叉树我用绿框圈了出来，对应的满二叉树有1个叶子节点，所以该位置表示的区间和对应区间就是 $[7, 7]$ ；
$i = 8$ 对应的满二叉树就是我们这整棵树，对应的满二叉树有8个叶子节点，所以该位置表示的区间和对应区间就是 $[1, 8]$ ；

那么我们怎么根据这个位置数字 $i$ （即元素下标）找到它为最底层最右边的叶子节点的满二叉树的大小呢？首先我们需要清楚，每一个满二叉树的叶子节点个数，都是2的整数次幂，也就是说每一个满二叉树的叶子节点个数用二进制表示都是最高位一个1，其余位都为0，比如满二叉树叶子节点为4个， $4)_{10}=(100)_{2}$ ，满二叉树叶子节点为8个， $8)_{10}=(1000)_{2}$ 。也就是说我们对于任何一个下标数字 $i$ ，这个数的二进制表示中有多少个1，它就由多少个满二叉树组成。例如 $6=4+2=(100)_{2}+(10)_{2}$ 由上图蓝色和橙色满二叉树组成。所以接下来，我们都知道，对于任何数比如这个下标 $i$ ，我们都可以把它写成 $2$ 的幂之和。有 $i=2^{j_{1}}+...+2^{j_{n}}，且2^{j_{1}}>2^{j_{2}}>...>2^{j_{n}}$ ，那么 $i$ 对应的它为最底层最右边的叶子节点的满二叉树的大小就是最小的那个 $2^{j_{n}}$ ，所以范围就是 $i-2^{j_{n}}+1,i]$ ，而 $j_{n}$ 就是 $i$ 对应的最右边的1右面有几个0也就是著名的 $l o w b i t (i)$ 。对应范围也就是 $[i - l o w b i t (i) + 1, i]$ 。
写成代码就是：

int lowbit(int x){
    
    
	return x&(-x);
}

lowbit具体操作含义之后补全。

2.求和操作

下面，我们来说一说求和操作，我们用树状数组求和，我们先只考虑最基本的前缀和，就是原数组第 $1$ 个元素到第 $i$ 个元素的和是多少，而这个和，我们就可以用我们的树状数组每个元素表示的区间和相加而得到。比如 $[1, 7]$ 的区间和就可以用之前样例树状数组的第4个元素( $[1, 4]$ )+第6个元素( $[5, 6]$ )+第7个元素( $[7, 7]$ )表示。因为这个元素 $i$ 我们可以表示成2的幂之和，而每个2的幂可以对应一个满二叉树的叶子节点个数，所以这些区间，就是一个个满二叉树叶子节点对应的区间。并且根据上文所讲，我们这个数 $i$ 对应二进制有多少个1，我们就可以把它拆成多少个满二叉树：

比如， $6)_{10}=(110)_{2}$ ，我们就可以把 $6$ 划分为两个二叉树，一个是100，一个是10，即下图的蓝框+橙框；
比如， $7)_{10}=(111)_{2}$ ，我们就可以把 $7$ 划分为三个二叉树，一个是100，一个是10，一个是1，即下图的蓝框+橙框+绿框；

所以设原数组为 $a$ ，设树状数组为 $t r e e$ ，对于任意的 $X=2^{i_{1}}+2^{i_{2}}+...+2^{i_{n}}，且2^{i_{1}}>2^{i_{2}}>...>2^{i_{n}}$ ，就可以把 $[1, X]$ 分为 $1,2^{i_{1}}]$ ， $2^{i_{1}}+1,2^{i_{1}}+2^{i_{2}}]$ ,…, $2^{i_{1}}+...+2^{i_{n-1}}+1,X]$ 这n个区间，也就有：

$a [1] + a [2] + . . . + a [X]$
$tree[2^{i_{1}}]+tree[2^{i_{1}}+2^{i_{2}}]+...+tree[2^{i_{1}}+...+2^{i_{n}}]$ 这一行将顺序颠倒并用X表示就成了下一行
$tree[X]+tree[X-2^{i_{n}}]+tree[X-2^{i_{n}}-2^{i_{n-1}}]+...+tree[X-2^{i_{n}}-2^{i_{n-1}}-...-2^{i_{2}}]$ 这行用作代码。

写成代码就是：

int getsum(int x){
    
    
	int ans=0;
	for(int i=x;i>0;i-=lowbit(i)){
    
    
		ans+=tree[i];
	}
	return ans;
}

3.更新操作

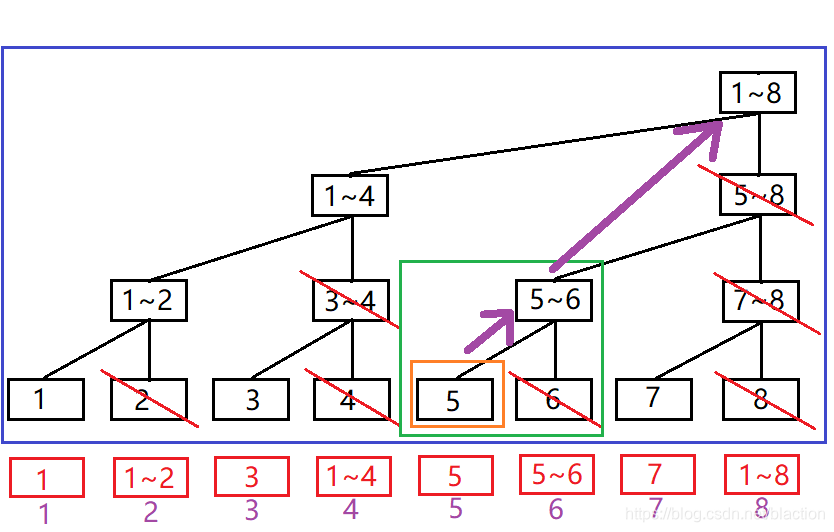
这里我就说一下单点更新，对于我们要修改的原数组的下标为X，那么我们就要将包含这个点的所有的满二叉树进行信息更新。比如我们对6进行更新，给原数组下标为5的元素加上一个值val，那么我们就需要依次对下图中的橙框对应满二叉树，绿框对应满二叉树，蓝框对应满二叉树进行信息更新，也就是需要tree[5]+val，tree[6]+val，tree[8]+val。那么对于X我们怎么找到包含它的更大一层二叉树的最右子节点的下标呢，我们只需要将X最低位的1向左挪动一位即可，也就是用当前下标加上lowbit(当前下标)。
在这里插入图片描述
写成代码就是：

void update(int loc,int val){
    
    
	for(int i=loc;i<=n;i+=lowbit(i)){
    
     //n是数组总长度
		tree[i]+=val;
	}
}

初稿可能有些乱，大佬们如果发现我哪里有错误欢迎指正，或者有什么更好的描述建议我都会悉心听取。