数学建模-几个微分方程建模并用python求解的栗子

#数学建模-几个微分方程建模并用python求解的栗子

建立微分方程模型一般分为以下三步

1. 根据实际要求确定研究的量（自变量、未知函数、必要的函数等），并确定坐标系

2. 找出这些量所满足的基本规律

3. 运用这些规律列出方程和定解条件

   下面直接上三种情况的例题叭：

栗子1：按规律直接建立方程

将某物体放置于空气中，在时刻t=0测量得它得温度为u0=150°C,10min后测量得它的温度为u1=100°C.要求建立此物体的温度u和时间t的关系，并计算20min后物体的温度.其中假设空气的温度保持为$$\frac{}{u}$$=24°C.

解决这道题首先需要我们知道牛顿冷却定律

假设物体在时刻t的温度为u=u(t),则由牛顿冷却定律，得到

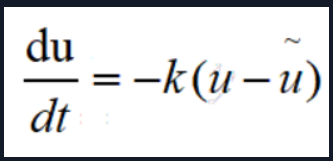
其中k>0，在这个条件下$$\frac{}{u}$$=24°c

当然大家用传统的微分方程也可以得到答案，但是这里我们强调如何用python作为工具来帮我解出这道题，不知道代码怎么写出来的可以看看我前面的帖子.

import sympy as sp
t=sp.symbols('t'); k=sp.symbols('k') #定义符号变量t,k
u=sp.var('u',cls=sp.Function) #定义符号函数
eq=sp.diff(u(t),t)+k*(u(t)-24) #定义方程
uu=sp.dsolve(eq,ics={
    
    u(0):150}) #求微分方程的符号解
print(uu)
kk=sp.solve(uu,k) #kk返回值是列表，可能由多个解
k0=kk[0].subs({
    
    t: 10.0, u(t):100.0})
print(kk,'\t',k0)
u1=uu.args[1] #提出符号表达式
u0=u1.subs({
    
    t:20, k:k0}) #代入具体值
print("20分钟后的温度: ",u0)

有两个注意点：

1. 符号变量和函数变量是一定要声明的，因为这是sympy解题的基本

2. 使用dsolve函数解出的结果或者最后的结果都是有C1、C2(任意常数)的，所以想要得到我们想要的结果我们还需要自己将t=0时的初始值代回得到常数的值

   所以

   uu=sp.dsolve(eq,ics={u(0):150})
   

   dsolve函数的参数ics其实是不会有实际性作用的(当然还可能有其他作用，所以还是要写着）

最后解出的结果是69.8413°.

栗子2：微元分析法

基本思想是通过分析研究对象的有关变量在一个很短时间内的变化规律，寻找一些微元之间的关系式

例题：有高为1m的半球形容器，水从它的底部小孔流出.小孔横截面积为1$$c{m}^2$$.开始时容器内盛满了水，求水从小孔流出过程中容器里水面的高度h(水面与孔口中心的距离)随时间t变化的规律.

由题意得R=$$1m$$

S=$$1c{m}^2$$

首先我们还是需要知道水力学知识

水从孔口流出的流量Q

$$Q=\frac{dV}{dt}=0.62S\sqrt{2gh}$$ 其中参数0.62被称为流量系数，g被称为重力加速度，S为孔口横截面积(单位：$$m^2$$), h为t时刻水面高度(单位:cm)

所以我们解出：

$$dV=0.000062\sqrt{2gh}dt$$

利用微元思想，我们知道在微小时间间隔[t,t+dt]内，水面高度由h降到h+dh(dh<0),容器中水的体积改变量近似为

$$dv=-\pi r^{2}dh$$

r为t时刻的水面半径

由上图的几何关系我们可以得到 $$R^2=r^2+(1-h{)}^2$$

R=1, so $$r^2=2h-h^2$$

所以

$$0.000062\sqrt{2gh}dt=\pi (h^2-2h)dh.$$
加上初始条件， 一个模型方程组就成功被建立了

接下里用python求解这个方程组即可

import sympy as sp
h=sp.symbols('h') #定义符号变量
t=sp.symbols('t',cls=sp.Function) #定义符号函数
g=9.8
eq=t(h).diff(h)-10000*sp.pi/0.62/sp.sqrt(2*g)*(h**(3/2)-2*h**(1/2)) #定义方程
t=sp.dsolve(eq,ics={
    
    t(1):0}) #求微分方程的符号解
t=sp.simplify(t)
print(t.args[1].n(9))  #这里args[1]是取出符号表达式 n(9)代表把等式pi的值代入得到新的等式

所以我们得到运行结果

$$t(h)=-1.5260.5042h^{\frac{3}{2}}+4578.1513h^{\frac{5}{2}}+10682.3530$$

栗子3：模拟近似法

该方法的基本思想是在不同的假设下模拟实际的现象，即建立模拟近似的微分方程，从数学上求解或分析解的性质，再去和实际情况作对比，观察这个模型能否模拟、近似某些实际的现象.

例题：(交通管理问题) 在交通十字路口，都会设置红绿灯.为了让那些正行驶在交叉路口或离交叉路口太近而无法停下的车辆通过路口，红绿灯转换中间还有亮起一段时间的黄灯.那么，黄灯应亮多长时间才最为合理呢？

题目分析：黄灯状态持续的时间包括驾驶员的反应时间、车通过交叉路口的时间以及通过刹车距离所需的时间.

1. 首先考虑刹车距离 设W为汽车的重量，u为摩擦系数.

由牛顿第二定律

$$\frac{w}{g}\cdot \frac{d^{2}x}{d{t}^2}=-uW$$

其中，g为重力加速度

化简可得： $$\frac{d^{2}x}{d{t}^2}=-ug$$

加入初始条件我们就得到了如下的二阶微分方程模型

用python代码

import sympy as sp
from sympy import  diff,dsolve,simplify
x=sp.symbols('x',cls=sp.Function)
t=sp.symbols('t')
g=sp.symbols('g')
u=sp.symbols('u')
eq=diff(x(t),t,2)+(u*g)
con={
    
    x(0):0}
x=dsolve(eq,ics=con)
print(simplify(x))

我们可以解出

$$x(t)=-\frac{1}{2}ug{t}^2+vot$$

刹车时 v=0 所以刹车所用时间 $$t0=\frac{v0}{ug}$$

代入我们解出的式子得

$$x(t0)=\frac{v{0}^2}{2ug}$$

2. 对于黄灯状态的时间T

   $$T=\frac{x(t0)+I+L}{v0}+T0$$

   T0是驾驶员的反应时间

   代入x(t0)得

   $$T=\frac{u0}{2ug}+\frac{I+L}{v0}+T0$$

   设参数值 T0=1s L=4.5m I=9m u=0.7

   我们对V0设置一个取值序列，来看黄灯时间T的值

from numpy import array
v0=array([45,65,80])
T0=1; L=4.5; I=9; mu=0.7; g=9.8
T=v0/(2*mu*g)+(I+L)/v0+T0
print(T)

[4.57988338 5.94530164 6.99965379]

最终就得到了不同法定速度下黄灯应该被设置的时间