动态规划图解(译)
前言
我曾经要帮一个朋友理解dynamic programming(动态规划,简称DP),所以会留心一些好的资源。我发现网上到处都是,但很多集中在对代码的讨论上,不能生动地阐明DP的工作原理。
斐波那契数(Fibonacci Number)
学习动态规划最经典的例子就是Fibonacci Number了。回忆下,Fibonacci Numbers是一个从1开始的序列,从第三项开始的每项都是前两项的和:
1,1,2,3,5,8,13,21,…
第n项递推公式的一种简单写法:
F 0 = 1 F 1 = 1 F n = F n − 1 + F n − 2
amp;F0=1amp;F1=1amp;Fn=Fn−1+Fn−2amp;F0=1amp;F1=1amp;Fn=Fn−1+Fn−2
F0=1F1=1Fn=Fn−1+Fn−2
用python整一个:
def fib(n):
# 最好检查下n是不是正数
if n == 0: return 1
if n == 1: return 1
return fib(n-1) + fib(n-2)
问题是,如果传入的n特别大,这个的函数执行时间会特别长。对10、20和30三个参数分别执行100次看下时间:
>>> import timeit
>>> timeit.timeit('fib(10)', number=100, globals=globals())
0.01230633503291756
>>> timeit.timeit('fib(20)', number=100, globals=globals())
0.3506886550458148
>>> timeit.timeit('fib(30)', number=100, globals=globals())
34.2489672530209
啊呀!从10到20运行时间翻了30倍,从20到30翻了100倍。为了找出原因,我们看下调用树。假设我们要计算F(5)。下图展示了主要问题是怎样依赖子问题来处理计算过程1。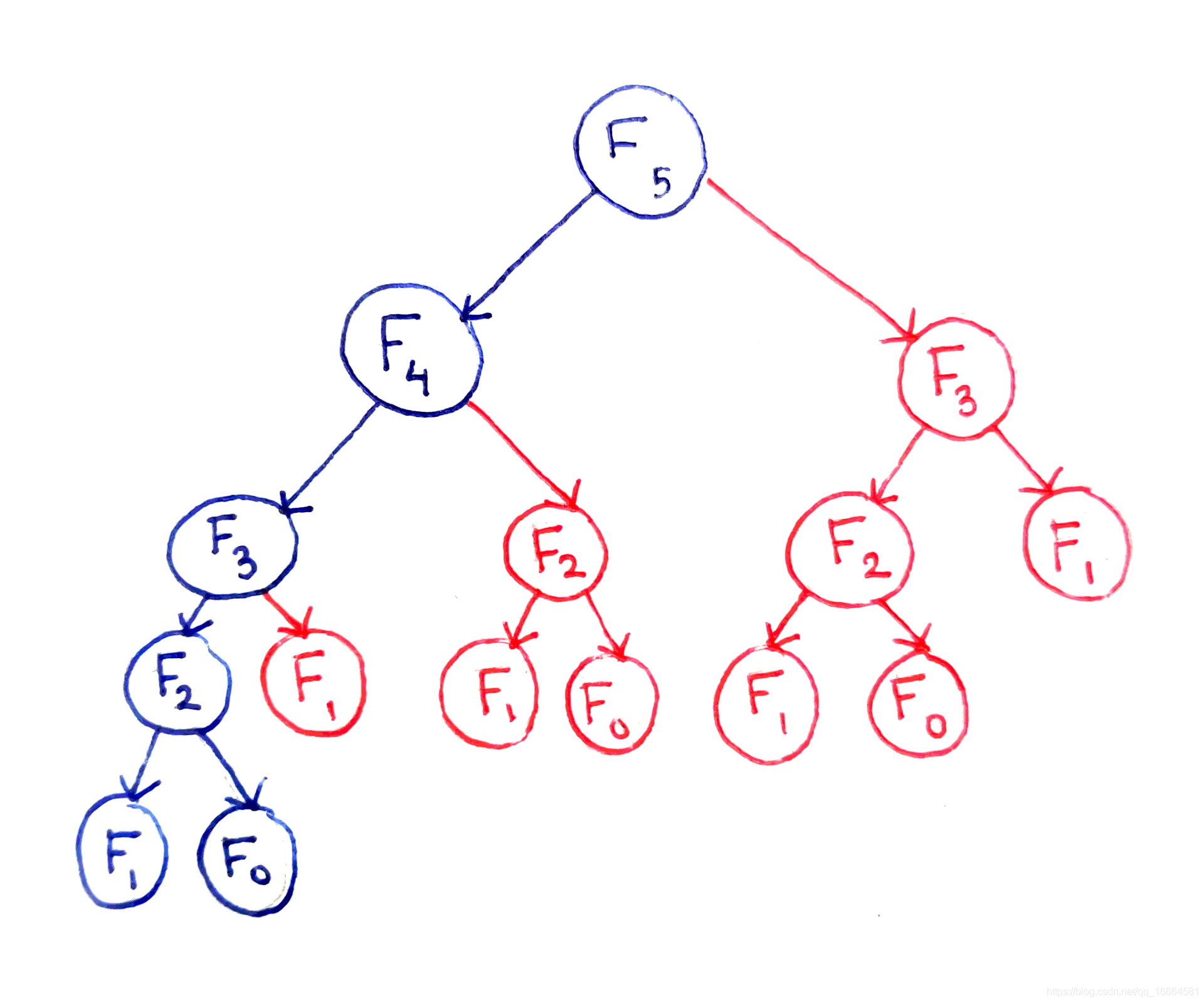
在斐波那契求解的过程中,每个子问题都依赖两个更小的子问题。这种天真的递归方法会导致许多子问题被重复计算两次以上。
这里最根本的问题是,某些子问题会被计算多次。比如,F(3)计算了两次,F(2)计算了3次,但是每次计算的结果是一样的。我不会对整个计算时间2做详尽的分析,但是这个算法执行完所消耗的时间是n的指数函数3。
如果一个问题具有这种特质4,DP就能派上用场。动态规划帮助我们解决一类递归问题,这些问题可以分解成一个个高度重叠的子问题。“高度重叠”指的是子问题一遍遍地重复出现。相反地,像归并排序这种递归算法,会先独立地排好列表的一 半,再把结果合并。这种把问题分解成子问题,并且产生的子问题不会重叠的算法,就是分治法。
使用记忆来避免重复计算子问题
避免一遍遍地重复计算子问题的方法就是缓存这些子问题的结果。工艺如下:
- 如果缓存包含了某次输入对应的计算结果,直接从缓存里返回那个值。
- 否则,计算结果并把它放入缓存中,把结果和输入相关联。下次需要求解相同自问题时,对应的结果已经在缓存中了。

通过缓存子问题的结果,许多递归调用就被清除了。
很容易把之前的递归算法转化成带记忆的版本:
def fib(n, cache=None):
if n == 0: return 1
if n == 1: return 1
if cache is None: cache = {}
if n in cache: return cache[n]
result = fib(n - 1, cache) + fib(n - 2, cache)
cache[n] = result
return result
看下执行时间:
>>> timeit.timeit('fib(10)', number=100, globals=globals())
0.0023695769486948848
>>> timeit.timeit('fib(20)', number=100, globals=globals())
0.0049970539985224605
>>> timeit.timeit('fib(30)', number=100, globals=globals())
0.013770257937721908
好,看起来是线性关系5了。但是空间复杂度呢?好的,为了计算F(n),我们需要计算F(n-1),F(n-2),一路下来到F(0)。有O(n)的子问题被缓存了。这意味着我们使用了O(n)的空间。
我们可以做的更好嘛?这次,我们可以。
自底向上法
让我们再看看调用树的图示,但是这次,每个子问题仅仅展示一次。这意味着如果两个不同的问题具有相同的子问题,会有两个箭头指向它。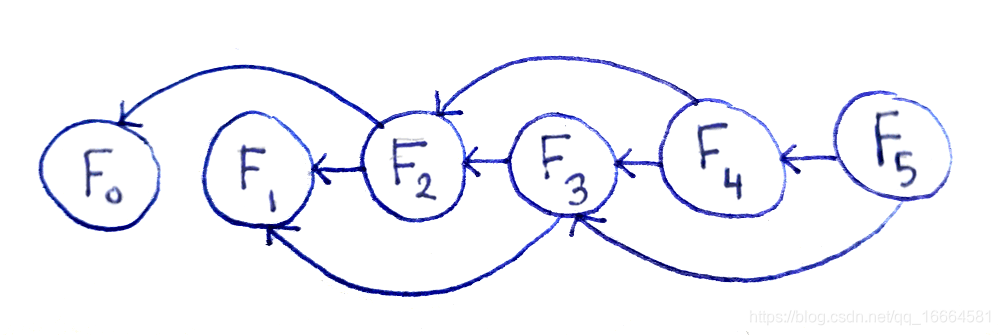
每个子问题仅出现一次使它们之间的关系更加清晰。
这种表示方法有很多好处。首先,我们看到有O(n)个子问题。然后,我们看到示意图是一个有向循环图6(简称DAG),意味着:
- 有顶点(子问题)和连接子问题的边(依赖)。
- 边有方向,它决定了边连接的一对子问题中谁依赖谁。
- 图没有循环,因此着只要顺着箭头走,从一个子问题不可能走回到原点。
DAG是线性化的,意味着你可你给顶点排序,排成只要顺着箭头的指向就可以按序遍历顶点的顺序。实际上,我们可以对子问题做排序,这样我们就能解决大的子问题之前获得它们依赖的子问题的结果。对于Fibonacci来说,子问题的顺序就是输入的顺序,意味着我们计算F(0),然后F(1),然后F(2),就这样直到F(n)。正如上面的示意图一样。
上面的DAG图也告诉我们,每个子问题都仅依赖之前刚刚算出的两个子问题。如果你正在计算F(m),你只需要F(m-1)和F(m-2)的结果。并且,如果你按照上面描述的顺序来计算子问题,你就能扔掉不再需要的值。
现在,我们可以实现一个算法:
- 在本地变量保存F(0)和F(1)(都是1)。在每个顶点这两个变量都会表示上两个Fibonacci数,正好我们需要它们来计算下一个Fibonacci数。
- 从2遍历到n,计算F(i)。每次的计算仅依赖于F(i-1)和F(i-2),所以在你做完之后,你可以把F(i-2)扔掉,因为你永远不会再用到它。为了下次迭代,更新本地变量,只保存F(i-1)和刚刚计算得出的F(i)。
用Python整一个:
def fib(n):
a = 1 # f(i - 2)
b = 1 # f(i - 1)
for i in range(2, n + 1): # n+1不被包括在循环里
# 老的“a”在此之后不会再用到
a, b = b, a + b
return b
java实现:
public int fib(int n) {
int num1 =1, num2 =1;
int res = 0;
if(n == 0 || n == 1)
return num1;
for (int i =2; i<=n;i++){
res = num1+ num2;
num1 = num2;
num2 = res;
}
return res;
}如果你试试这个版本的运行时间,你会发现它也是线性的。还有,由于在每次迭代中我们仅仅保存了两个之前计算的结果,这个版本只耗费了常数空间,比我们之间的版本减少了很多。由于这种方法通过解决“更小的”子问题来构建更大的,我们把它称作自底向上法。
房屋盗窃问题(House Robber Problem)
现在我们有了一套方法来解决那些具有高度重叠子问题的递归问题,不妨试试一个更复杂的问题。在房屋盗窃问题中,你是一个偷儿,找到一片别墅区打算开工。每间编号为i的别墅都有价值v(i)7的东西可偷。然而,别墅都部署了安全系统,如果你偷了两间相邻的别墅就会被逮到。你从这片别墅区最多能偷到多少钱?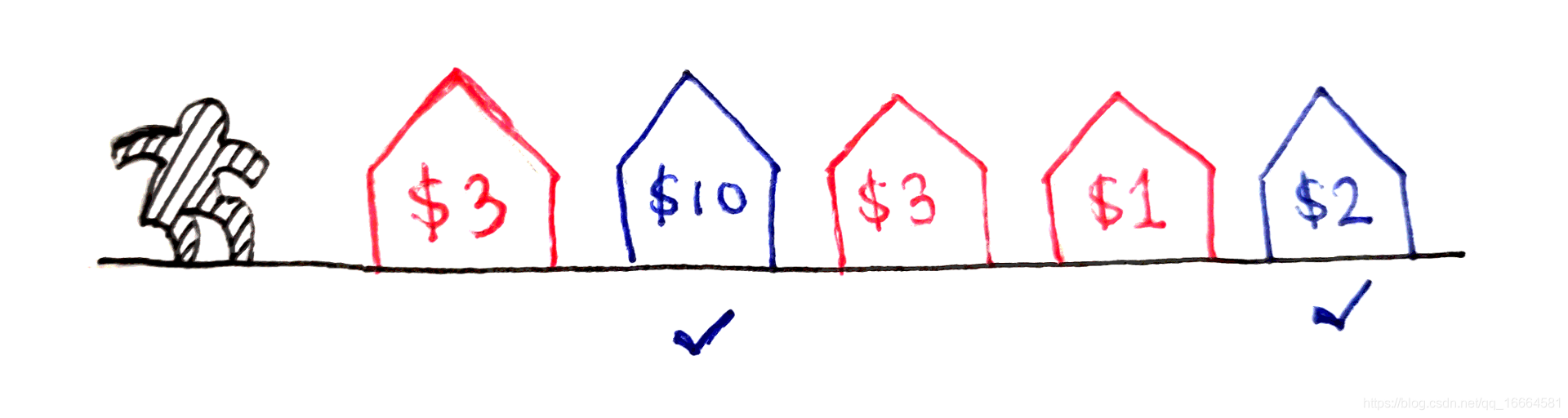
在这个例子中,偷儿应该偷第二和第五个别墅,这样搞到的钱最多。
举个例子,如果别墅的价值分别是3、10、3、1、2,你最多能从第二间和第五间偷到总共12。注意在这个例子中你能偷任何房间,但是最好别偷相邻的。
分解成子问题
求解动态规划问题时,第一个步骤就是确认子问题,这也是至关重要的一步。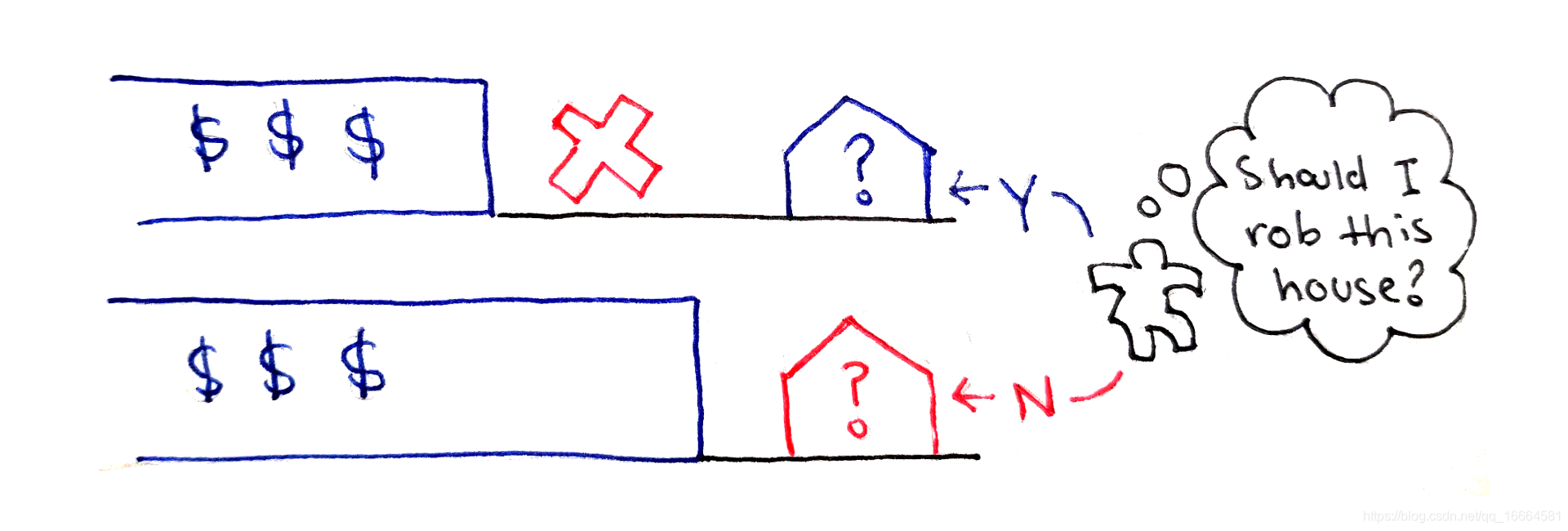
在每个子问题求解中,偷儿都必须决定抢哪间,不抢哪间。
当你进入房间i时,你有两个选择:
- 偷i,然后计算从前面i-2间里偷出的最大值,因为i-1不能再偷了。偷完把v(i)加到总赃款中。
- 不偷i,这样你可以自由地选择前面的i-1间来使得赃款最大化。因为没偷,就不能往总赃款里加值。
你的选择决定了你的钱途。
定义递推关系
为了更准确地描述上述直觉,我们显然可以定义出具有如下属性的函数:
- 函数应当有一些整数输入。这允许我们把输入值和已经得到的计算结果关联起来,此外,提升这个函数的定义顺序。
- 你寻找的解法应当从这个函数中得到。否则,这个函数实际上不能帮我们找到想要的解。
- 函数可以调用自己
这个函数被称为递归函数因为它可以调用自己。
对于房屋偷盗问题,上述直觉可以转换成下面的递推关系。定义f(i)为从0到i个别墅中偷到的最大值。
f ( i ) = m a x { f ( i − 2 ) + v i f ( i − 1 ) f(i) = max
{f(i−2)+vif(i−1){f(i−2)+vif(i−1)
f(i)=max{f(i−2)+vif(i−1)
我们最终想要的解仅仅是f(n-1),n是别墅的总数量(假设房间编号从0开始)
自底向上实现
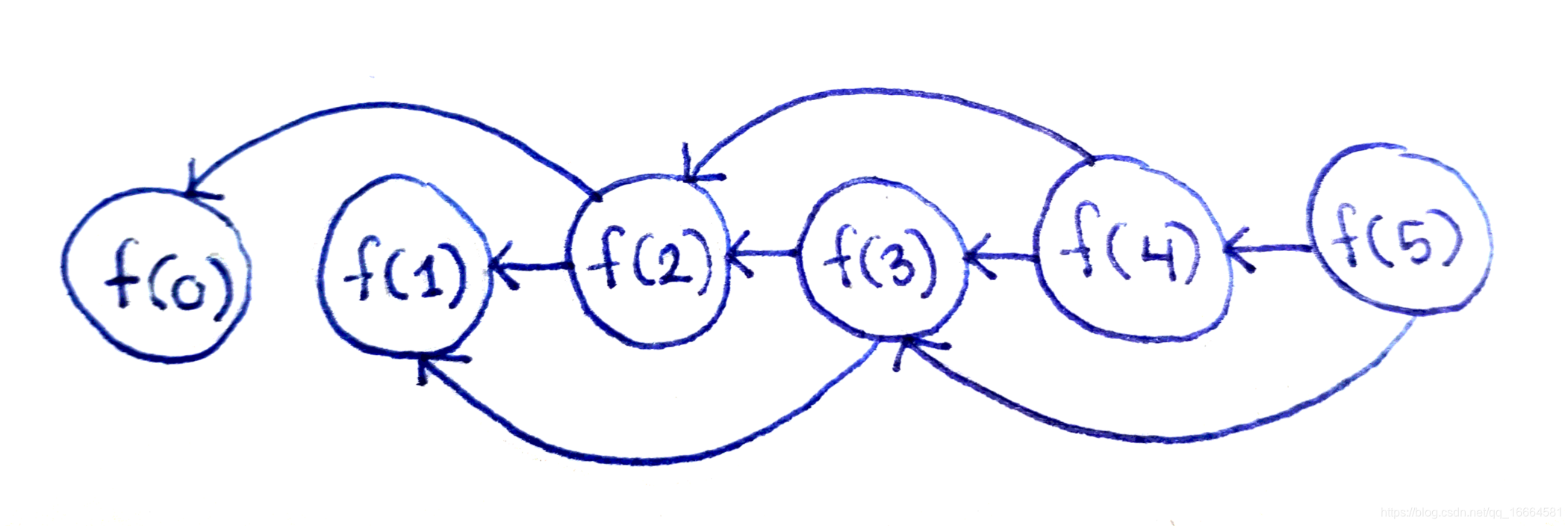
房屋偷盗问题的DAG和Fibonacci的DAG是一样的!
我们用递推关系画出了DAG。它看起来和Fibonacci的DAG是一样的。每个子问题f(i)取决于前两个子问题f(i-1)和f(i-2)。而且,有n个子问题:f(0)、f(1),…,f(n-1)。这意味着我们可以在O(n)时间内解决这个问题,并且在O(1)的空间内,按照索引递增的顺序计算子问题,每次只保存最后两个值。
def house_robber(house_values):
a = 0 # f(i - 2)
b = 0 # f(i - 1)
for val in house_values:
a, b = b, max(b, a + val)
return b
java实现:
public class HouseRobberProblem {
public static void main (String[] args) {
HouseRobberProblem hr = new HouseRobberProblem();
int[] houses = new int[]{3,10,3,1,2};
System.out.println(hr.houseRobber(houses,4));
System.out.println(hr.houseRobber(houses,0));
System.out.println(hr.houseRobber(houses,1));
System.out.println(hr.houseRobber(houses,2));
System.out.println(hr.houseRobber(houses,3));
int[] houses1 = new int[]{3,10,3,1,2,100};
int[] houses2 = new int[]{3,10,3,1,2,1};
System.out.println(hr.houseRobber(houses1,5));
System.out.println(hr.houseRobber(houses2,5));
}
public int houseRobber(int[] houseVals, int n) {
int res0 = houseVals[0];
int res1 = Math.max(houseVals[0], houseVals[1]);
int res = 0;
if (n == 0) {
return res0;
}
if (n == 1) {
return res1;
}
for (int i = 2; i<= n; i++) {
res = Math.max(res0 + houseVals[i], res1);
res0 = res1;
res1 = res;
}
return res;
}
}正如DAG预示的那样,它的实现方式几乎和Fibonacci一样,只有计算过程中前两个值的组合方式不一样。
零钱构成问题(The Change Making Problem)
前两个问题都是“一维”问题,可以通过递归线性的子问题序列来解决。下面的问题具有“二维”结构。
**零钱构成问题8**问的是假如你有一堆硬币(只有给定的几种面值),你可以用最小数量的硬币来组合成一个特定的金额吗?这个最小数量是多少?假设每种面值的硬币都有无数个。把这些面值计做d(i),待组合的金额计为c。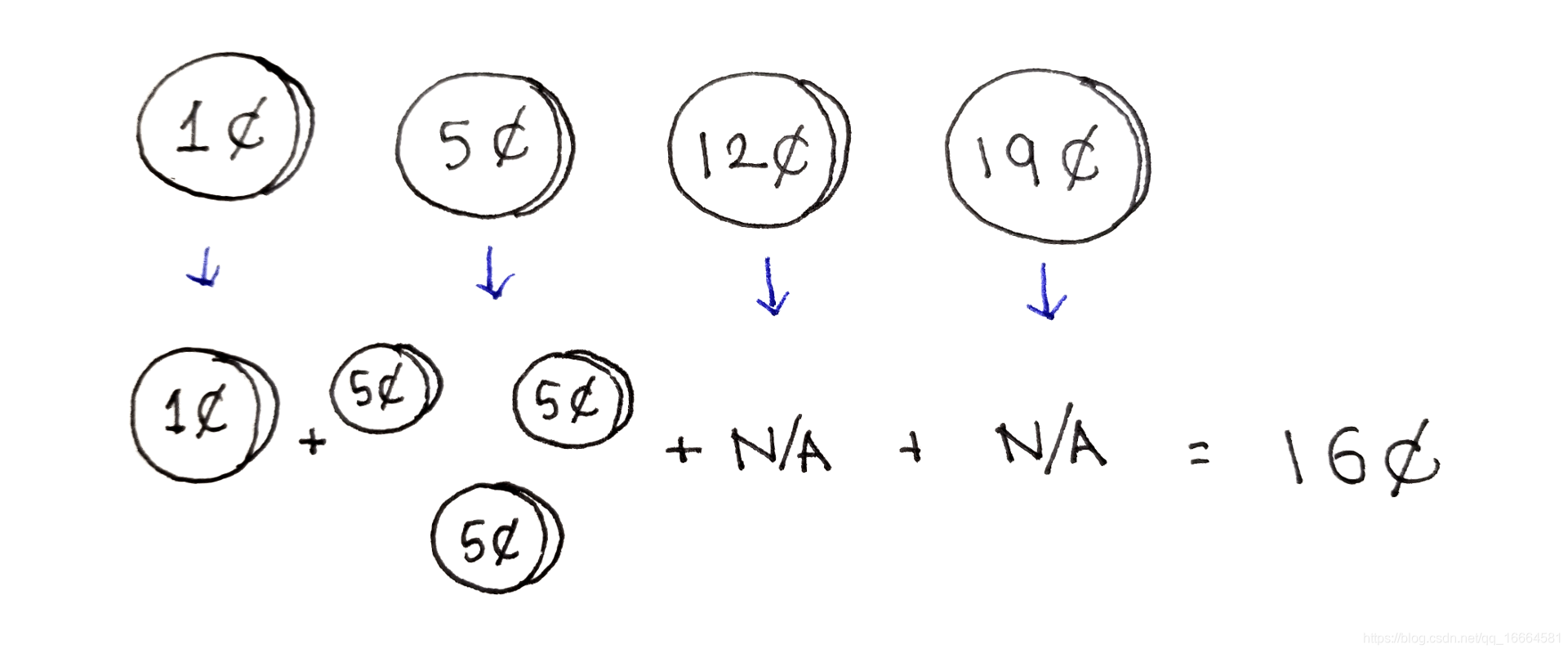
在这个例子中,最优的选择是使用1个1¢和3个5¢。
举个例子,假设我们有1¢9、5¢、12¢和19¢几种面值,我们想构成16¢。使用硬币的最小数量是4:3个5¢和1个1¢。要注意的是,使用最大面值的硬币未必是总最好的,比如这里用1个12¢的,还需要4个1¢的,总共是5个。
我们马上可以得到几个结论:
- 我们假设所有给定面额下面只有一个硬币。从技术的角度来讲,没必要做出这种限制,但是限制条件有利于理性分析问题。
- 我们假设给定的面值按照从小到大排序。从乱序开始?可以,但没必要,我们现在不用关心排序问题了。
- 第一个面值必须是1。只有这样才能组合出所有的正数。
分解成子问题
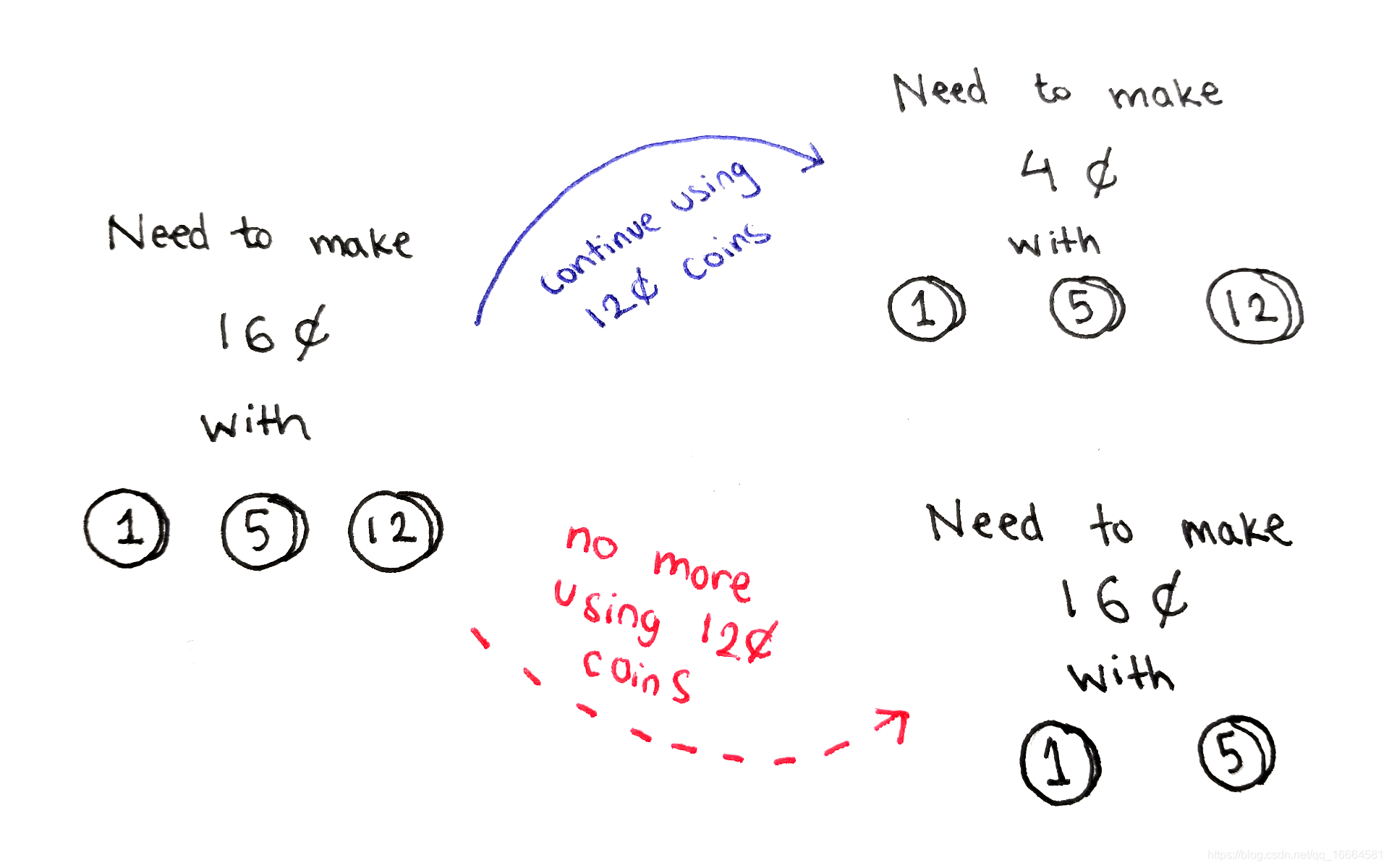
在每个迭代中,我们可以继续使用最高面值,也可以转移到次高面值。
在算法的每次迭代中,我们都会考虑到给定面值的子集和我们要构成的金额。这给我们两个选择:
- 使用一个最高面值的硬币。目标金额减少,然后我们使用相同的面值和新的目标金额。这样我们还有机会再次使用最高面值。由于使用了硬币,硬币使用数量+1。
- 不使用最高面值的硬币。目标金额不变,但是可选面值少了一种。通常在搞定最高面值后,要使用次高面值时选择这个选项。由于没使用硬币,硬币使用数量不变。
产生使用硬币数最少的那个选项是最优的。
注意两个选项只能二选一。比如当只剩一种额度可选时,我们只能用它。同样的,如果当前额度大于目标金额,我们就要停止该额度。
定义递推关系
我们想定义的函数需要两个输入:给定面值的子集,待构成的目标金额。考虑到面值是递增给出的,我们只需要用一个整数来表示当前考虑的面值。比如,整数i代表我们仅仅考虑d(0)、d(1),…,d(i),i之后的不考虑。
有了这两个输入,我们可以定义函数f(i, t)来表示用面值i构成目标金额t所使用的硬币的最小数量。
f ( i , t ) = m i n { f ( i , t − d i ) + 1 f ( i − 1 , t ) f(i,t) = min
{f(i,t−di)+1f(i−1,t){f(i,t−di)+1f(i−1,t)
f(i,t)=min{f(i,t−di)+1f(i−1,t)
我们要求就是f(n-1,c),n是题设给定的面值种类数,c是初始目标金额。
检查DAG
因为递推关系中有两个整数输入,我们可以把子问题表示成二维表,第一个输入(即考虑的面值种类数)作为x轴的索引,第二个输入(目标金额)作为y轴的索引。
正确的连接取决于面值的可用。比如下面的例子,有三种面值:d(2)=3,d(1)=2,d(0)=1,从左到右依次按照面值降序。最终的目标金额是5,但是所有的中间金额是从底向上递减。这样,我们的答案就在这张自底向上的表中。
这个问题的DAG有点复杂,所以我们一步步考虑。首先我们画一个二维结构示意图并展示出目标解。每个单元格由两个数字索引:(i,t),i代表当前考虑的最大面值,t代表当前目标金额。
由于递推关系有两个输入,DAG可以表示成二维表。目标解在左下角。
在这个单元格里,两个选项都是可用的。一则可以使用一个最高面值的硬币,然后单元格向上移动,再则可以忽略该面值,把单元格向右移动: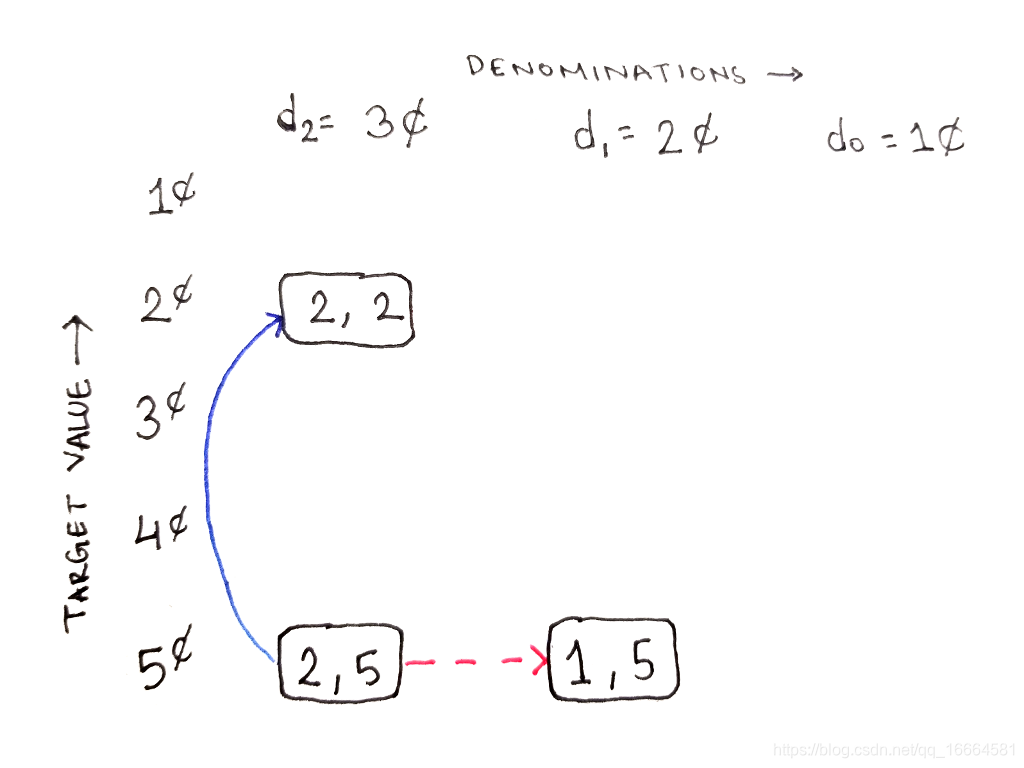
初始情况下两个选择都是可用的,所以我们必须考虑两个子问题。实线箭头代表使用当前最高面值,虚线箭头代表忽略它。
考虑子问题(1,5),表示仅使用2¢和1¢来构造5¢,我们依然有两个选择。子问题中的1关联着d(1),意味着只有d(1)和d(0)可用。这要求我们考虑子问题的两个子问题: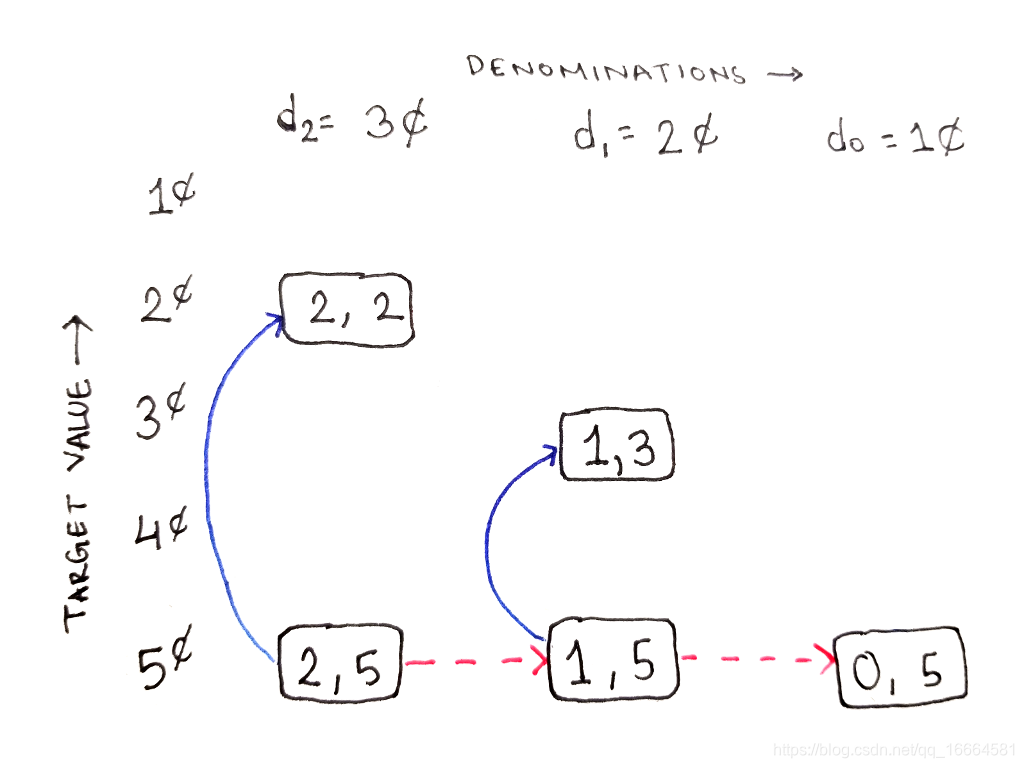
子问题(1,5)依旧有两个选择
然而,考虑子问题(2,2),表示用所有三种面值构造2¢,这里用不到最高面值3¢。所以我们只有一个选择就是忽略该面值,单元格向右移动: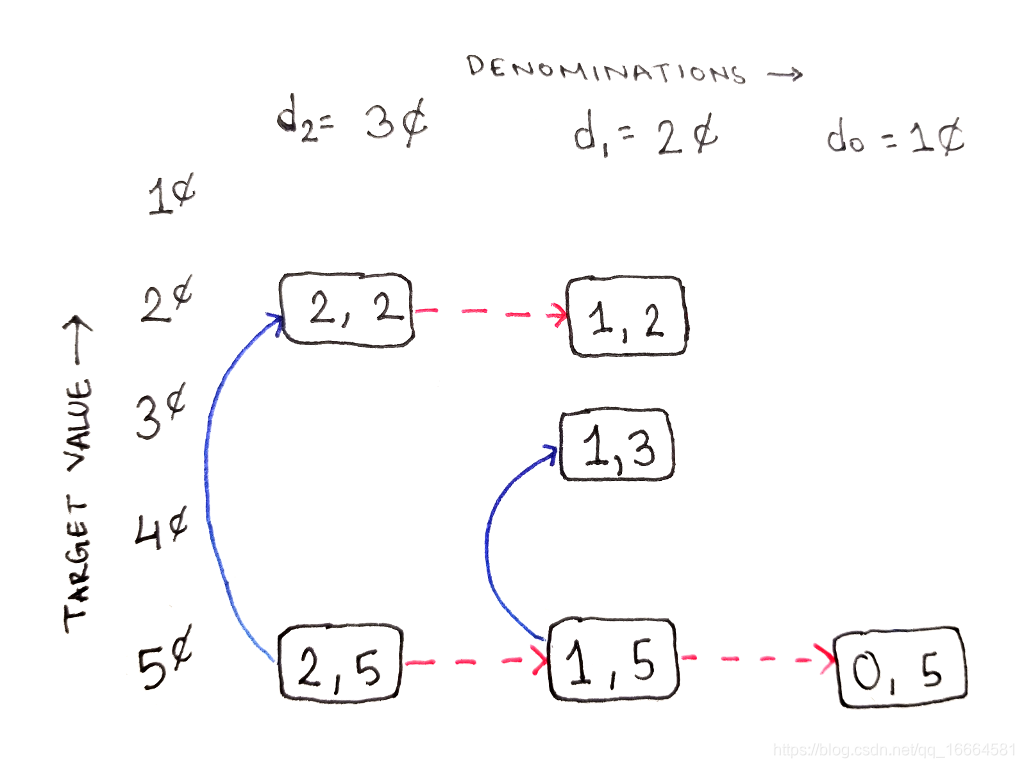
子问题(2,2)只有一种选择
相似地,考虑子问题(0,5),只使用1¢来构造5¢,我们不得不使用当前最大面值,因为没有其他面值可选了。实际上,考虑最右侧的依赖链,我们能做的只有向上移动单元格,因为没法向右移了: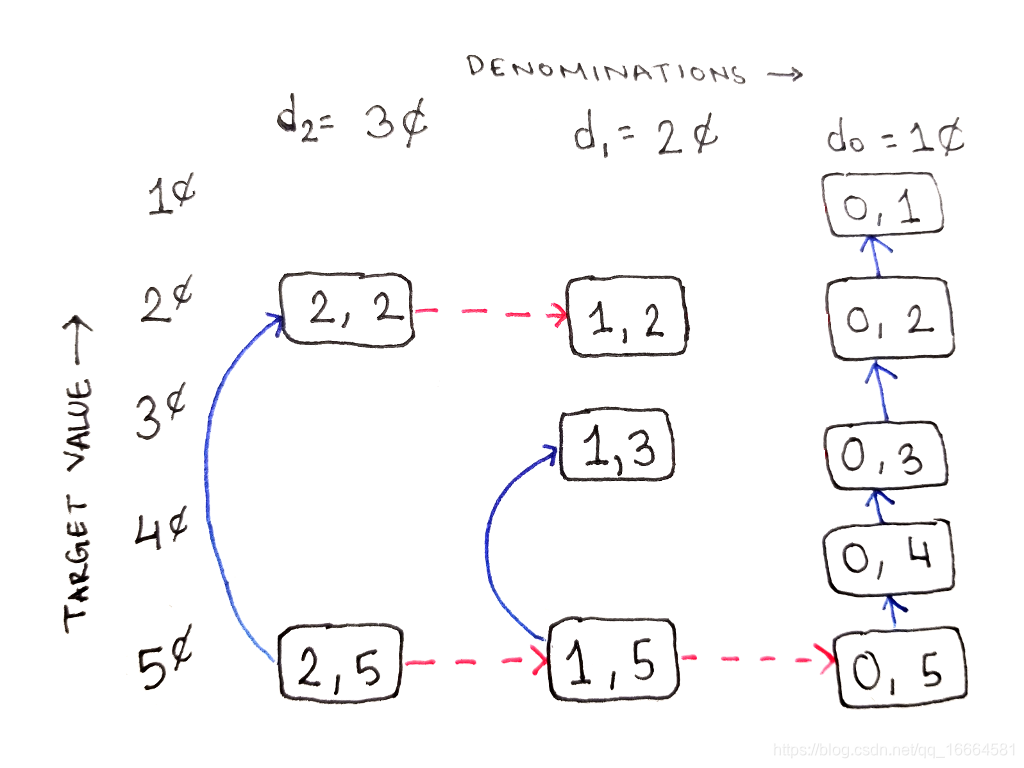
最右侧的单元格只有一种选择。每次移动单元格,我们使用1个1¢硬币的同时,目标金额也会减少1。
用这种方法表示剩下的结构。浅色的单元格表示没有用到的子问题,它们的依赖关系也没有展示。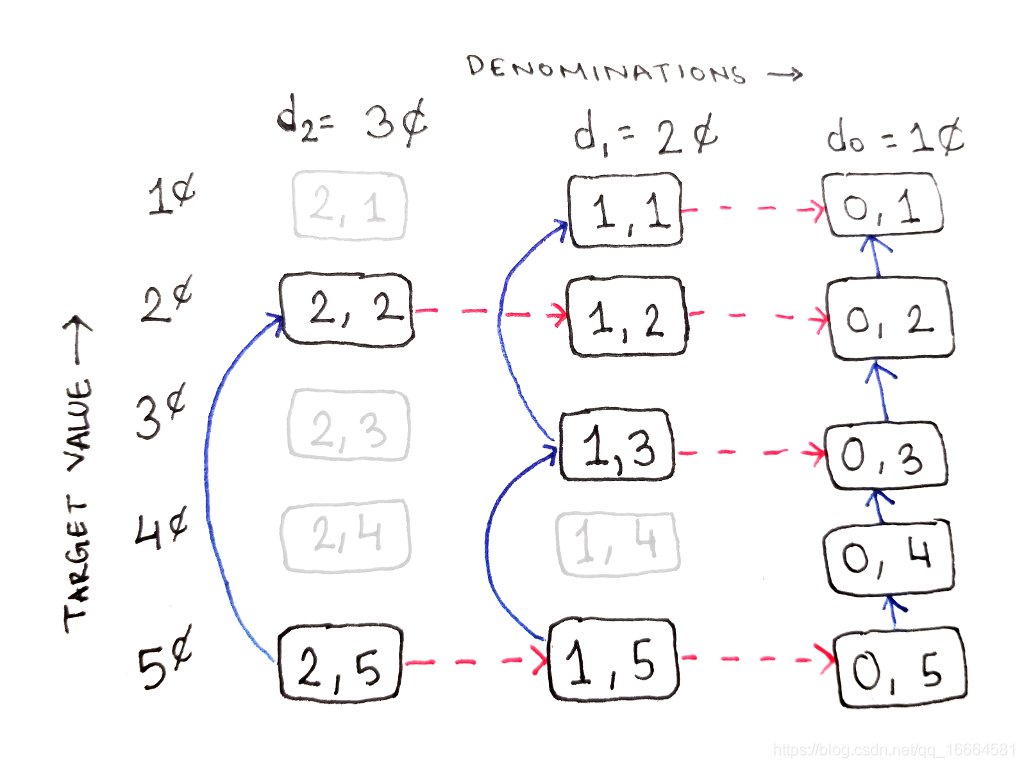
依赖图的最终表结构,浅色单元格表示没有用到的子问题。
作为练习,也请画出未用到子问题的依赖箭头。比如,(2,4)子问题怎样用3种面值表示4¢,它的子问题又是什么呢?
自底向上实现
在这个DAG中,我们看到有的单元格仅仅依赖同列的其他单元格和右侧单元格。这意味着我们可以按照以下顺序计算子问题:
- 从最右侧的列开始,一次计算一列。
- 对于每一列,自底向上计算。
- 只保存上次计算的列,用于计算下一列。
然而,并不是每一列的所有值都要计算。这意味着,我们不需要完整计算每一列。不幸的是,确定一列中哪些值需要计算并不容易。
所以,虽然我们可以实现一个自底向上的算法,为了避免不必要的计算,我们用记忆化来代替。当出现很大的面值时,记忆化可以避免很多计算。
记忆化实现
记忆化实现可以从上面的递推关系中直接得到。技巧性的部分是我们何时不用做特定的选择。如果一个分支没有验证,我们使用math.inf作为该分支的值。这会导致min()选择其他分支的值。
import math
def coins(denominations, target):
cache = {}
def subproblem(i, t):
if (i, t) in cache: return cache[(i, t)] # memoization
# Compute the lowest number of coins we need if choosing to take a coin
# of the current denomination.
val = denominations[i]
if val > t: choice_take = math.inf # current denomination is too large
elif val == t: choice_take = 1 # target reached
else: choice_take = 1 + subproblem(i, t - val) # take and recurse
# Compute the lowest number of coins we need if not taking any more
# coins of the current denomination.
choice_leave = (
math.inf if i == 0 # not an option if no more denominations
else subproblem(i - 1, t)) # recurse with remaining denominations
optimal = min(choice_take, choice_leave)
cache[(i, t)] = optimal
return optimal
return subproblem(len(denominations) - 1, target)
java实现:
public class TheChangeMakingProblem {
public static void main(String[] args) {
int[] deno1 = new int[]{1, 2, 3};
TheChangeMakingProblem change = new TheChangeMakingProblem();
System.out.println(change.coins(deno1,2,5));
int[] deno2 = new int[]{1,5,12,19};
System.out.println(change.coins(deno2, 3, 16));
}
public int coins(int[] denominations, int idx, int target) {
Map<String, Integer> cacheMap = new HashMap<>();
String cacheKey = String.valueOf(idx) + "," + String.valueOf(target);
if (cacheMap.containsKey(cacheKey)) {
return cacheMap.get(cacheKey);
}
int val = denominations[idx];
int choiceTake = Integer.MAX_VALUE;
int choiceLeave = Integer.MAX_VALUE;
int optimal = Integer.MAX_VALUE;
if (val > target) {
choiceTake = Integer.MAX_VALUE;
} else if (val == target) {
choiceTake = 1;
} else {
choiceTake = 1 + coins(denominations, idx, target - val);
}
if (idx == 0) {
choiceLeave = Integer.MAX_VALUE;
} else {
choiceLeave = coins(denominations, idx - 1, target);
}
optimal = Math.min(choiceTake, choiceLeave);
cacheMap.put(cacheKey, optimal);
return optimal;
}
}尽管我们用记忆化减少了计算量,它还是取决于图中子问题的总数。这个算法的时间和空间复杂度都是O(nc),n是面值的种类数,c是目标金额。
总结
总结一下,动态规划是一种能高效解决具有某种特殊结构(有高度重叠的子问题)的递归问题的技术。运用动态规划时,遵循以下步骤:
- 定义子问题。通常情况下,每个步骤都只有一个选择,每个选择依赖一个更小的子问题。
- 写出递推关系。
- 决定子问题的顺序。画出依赖图总是有用的,依赖图可能是一行,也可能是个表格。
- 通过按顺序解决子问题来实现递推关系,在每个步骤里只保存你需要的结构。记忆化是一种可选手段。
我们看到这个方法解决了三个问题:Fibonacci数,房屋偷盗问题和零钱构成问题,我鼓励你在更多问题上去实践。如果你想让我实践更多问题和解决方案,请告诉我!
参考:https://blog.csdn.net/qq_16664581/article/details/89598243