hello,你好呀,我是灰小猿,一个超会写bug的程序猿,
今天和大家分享一个递归经典算法案例---“汉诺塔”。

汉诺塔问题回顾
汉诺塔(Tower of Hanoi)源于印度传说中,大梵天创造世界时造了三根金钢石柱子,其中一根柱子自底向上叠着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
这是一个著名的问题,几乎所有的教材上都有对这个问题的介绍。由于条件是:
借助一个中转柱,使起始柱中按照规则排放的盘子移动到终点柱,且一次只能移动一个盘,且不允许大盘放在小盘上面,所以64个盘的移动次数是:18,446,744,073,709,551,615
这是一个天文数字,若每一微秒可能计算(并不输出)一次移动,那么也需要几乎一百万年。我们仅能找出问题的解决方法并解决较小N值时的汉诺塔,但很难用计算机解决64层的汉诺塔。
在平常的编程练习过程中,汉诺塔问题也是一个十分常见的算法案例。今天我就和小伙伴们具体分析一下汉诺塔问题的解决方案。
首先我们来看一个三层汉诺塔的图解,来对汉诺塔问题的解决有一个简单的了解:
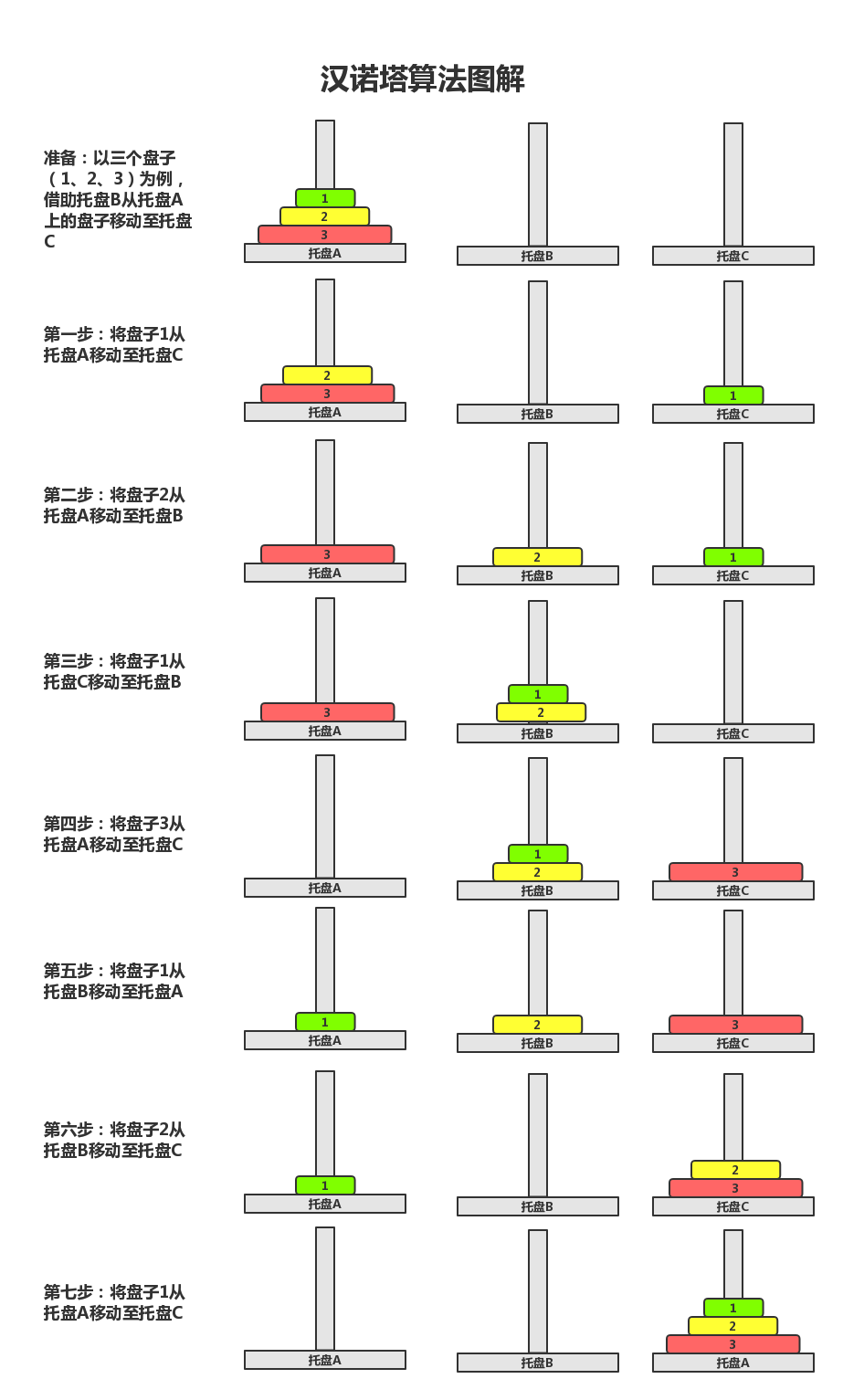
如上图所示,我们可以看出,当盘子的数量只有一个的时候,我们可以直接将盘子移动到目标盘,在进行三层汉诺塔问题的解决时。我们先将最上方的两个盘子借助目标盘移动至中转盘,再将最大的盘子移动至目标盘,之后再将中转盘上的第一个盘子移动至起始盘,这个时候我们就可以将二号盘移动至目标盘,最后将起始盘上的一号盘移动至目标盘。
由此我们可以总结出n层汉诺塔的解决方案:
将前n-1个盘子借助当前的中转盘(不一定是B托盘)移动至相邻的空托盘上,再将第n个盘子移动至目标盘,之后重复上述步骤直至将所有的盘子都移动至目标盘。在这个也用到了函数方法的递归思想。
接下来分别使用java和Python向大家演示一下n阶汉诺塔的求解方法:
Java求解汉诺塔
package 汉诺塔算法;
public class Hanoi {
public static void main(String[] args) {
// TODO Auto-generated method stub
Hanoi h = new Hanoi();
char a = 'A';
char b = 'B';
char c = 'C';
int count = h.hanoi(3, a, b, c);
System.out.println(count);
}
/**
* 汉诺塔问题
* @param n 阶数
* @param a 起始柱
* @param b 中转柱
* @param c 目标柱
* @return 移动次数
* */
public int hanoi(int n,char a,char b,char c) {
if (n == 1) {
move(a, c);
} else {
hanoi(n-1, a, c, b);
move(a, c);
hanoi(n-1, b, a, c);
}
//汉诺塔的移动次数为(2**n)-1
return (int) Math.pow(2, n)-1;
}
public void move(char a,char b) {
System.out.println(a + "--->" + "b");
}
}
Python求解汉诺塔
i = 1 # 定义全局变量记录次数
def move(n, a, c):
global i
print("第{}步:将编号为{}的盘子从{}--->{}".format(i, n, a, c))
i += 1
def hanoi(n,a,b,c):
#a,b,c分别是三根柱子,n为套在a柱上的圆圈个数
if n == 1:
move(n, a, c)
else:
hanoi(n-1, a, c, b)
move(n, a, c)
hanoi(n-1, b, a, c)
if __name__ == '__main__':
n = int(input("请输入盘子数量:"))
hanoi(n, "A", "B", "C")
好了,关于汉诺塔问题的讲解就和小伙伴们分享到这里,有不足的地方还希望大家提出指正,大灰狼陪你一起进步!
