Spark计算工具类

Vector

vectors.txt

1 2.3 4.5
3 3.1 5.6
4 3.2 7.8

处理vectors.txt文件RDD[String]->RDD[Vector]

package com.yasuofenglei

import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.SparkConf
import org.apache.spark.SparkContext

object Driver01 {
  def main(args: Array[String]): Unit = {
    //创建向量类型，传入的类型是Double类型，如果是Int类型，会自动转换
    val v1=Vectors.dense(1,2,3.1,4,5)
    //
    val v2=Vectors.dense(Array[Double](1,2,3,4))
    
    
    
    val conf=new SparkConf()
    conf.setMaster("local").setAppName("wordcount")
    val sc=new SparkContext(conf)
    val data=sc.textFile("d://data/ml/vectors.txt",2)
    //RDD[String]->RDD[Array[String]]->RDD[Array[Double]]
    val r1=data.map{_.split(" ").map{num => num.toDouble}}
    .map{arr =>Vectors.dense(arr)}
    r1.foreach { println}
    
  }
}

向量标签

package com.yasuofenglei

import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.SparkConf
import org.apache.spark.SparkContext

object Driver02 {
  def main(args: Array[String]): Unit = {
    val v1=Vectors.dense(2.2,3.1,4.5)
    //创建一个向量标签，1标签值
    val lb1 = LabeledPoint(1, v1)
    println(lb1)
    println(lb1.features)//获取向量标签中的向量
    println(lb1.label)//获取标签值
    
    
    val conf=new SparkConf()
    conf.setMaster("local").setAppName("wordcount")
    val sc=new SparkContext(conf)
    val data=sc.textFile("d://data/ml/vectors.txt",2)
    
    
    val r1=data.map{line=>
      val info=line.split(" ")
      val label=info.head.toDouble
      val features=info.drop(1).map{
        num => num.toDouble
      }
      LabeledPoint(label,Vectors.dense(features))
    }
    
    r1.foreach{println}
  }
}

Spark计算工具类

package com.yasuofenglei

import org.apache.spark._
import org.apache.spark.mllib.linalg._
import org.apache.spark.mllib.stat.Statistics

/**
 * Spark计算工具类
 */
object Driver03 {
  def main(args: Array[String]): Unit = {
    var conf=new SparkConf().setMaster("local").setAppName("statistic")
    var sc=new SparkContext(conf)
    val r1=sc.makeRDD(List(1,2,3,4,5))
    //RDD[Int]->RDD[Vector]
    val r2=r1.map{ num => Vectors.dense(num)}
    val result=Statistics.colStats(r2)
    
    println(result.max)
    println(result.min)
    println(result.mean)//均值
    println(result.variance)//方差
    println(result.count)
    println(result.numNonzeros)//不为0的元素个数
    println(result.normL1)//计算曼哈顿距离
    println(result.normL2)//计算欧式距离
    
  }
}

欧氏距离

欧氏距离（Euclidean Distance）
在二维和三维空间中的欧氏距离的就是两点之间的距离。
二维空间的欧氏距离：
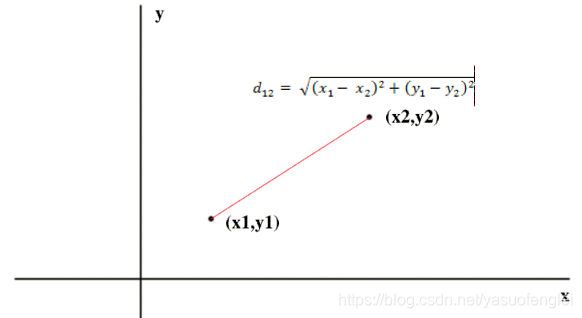二维平面上两点a(x1,y1)与b(x2,y2)间的欧氏距离：

三维空间两点a(x1,y1,z1)与b(x2,y2,z2)间的欧氏距离：

两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧氏距离：

也可以用表示成向量运算的形式：

R计算欧氏距离
在R中计算距离的函数为dist()，比较直接的用法是dist(x,method=“euclidean”)即为计算欧式距离，其余可选的参数还有"maximum", “manhattan”, “canberra”, “binary” ,“minkowski”，lz调整这个参数就能得到lz要的距离
案例1：R计算欧氏距离

a = c(1,1,3)
b = c(4,5,1)
distance=sqrt(sum((a-b)^2));distance
[1] 5.385165

或者：

dist(rbind(a,b), method= “euclidian”)
a
b 5.385165

即样本a和样本b之间的距离为：5.385165

案例2：R计算多样本间的欧式距离

a=matrix(rnorm(15,0,1),c(3,5))
a
[,1] [,2] [,3] [,4] [,5]
[1,] 1.8094360 -0.7377281 -2.2285413 0.6091852 -0.1709287
[2,] -0.7308505 -0.3415692 -0.7755661 1.4363829 -0.5686896
[3,] 1.2290613 1.7541220 -0.8617373 0.3623487 -1.1996104
dist(a,method=“euclidian”)

结果：

-	1	2
2	3.092508
3	3.087624	3.129251

第一行样本和第二行样本的距离：3.092508
第一行样本和第三行样本的距离：3.087624
第二行样本和第三行样本的距离：3.129251

曼哈顿距离(Manhattan Distance)

出租车距离或曼哈顿距离(Manhattan Distance)是由十九世纪的赫尔曼·闵可夫斯基所创词汇 ，是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。

下图中：

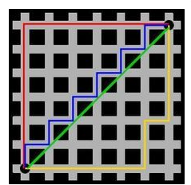
红线代表曼哈顿距离，
绿色代表欧氏距离，也就是直线距离，
而蓝色和黄色代表等价的曼哈顿距离。曼哈顿距离–两点在南北方向上的距离加上在东西方向上的距离，
即d(i，j)=|xi-xj|+|yi-yj|。

对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离因此曼哈顿距离又称为出租车距离，曼哈顿距离不是距离不变量，当坐标轴变动时，点间的距离就会不同。

曼哈顿距离示意图在早期的计算机图形学中，屏幕是由像素构成，是整数，点的坐标也一般是整数，原因是浮点运算很昂贵，很慢而且有误差，如果直接使用AB的欧氏距离(欧几里德距离:在二维和三维空间中的欧氏距离的就是两点之间的距离距离)，则必须要进行浮点运算，如果使用AC和CB，则只要计算加减法即可，这就大大提高了运算速度，而且不管累计运算多少次，都不会有误差。

例如在平面上，坐标(x1, y1)的i点与坐标(x2, y2)的j点的曼哈顿距离为:
d(i,j)=|X1-X2|+|Y1-Y2|.

案例：R计算两点间的曼哈顿距离

a<-c(1,2)
b<-c(5,8)
dist(rbind(a,b),method=“manhattan”)
a
b 10

结果：a样本和b样本的曼哈顿距离=10

切比雪夫距离

切比雪夫距离(Chebyshev Distance)，在数学中，切比雪夫距离或是L∞度量是向量空间中的一种度量，二个点之间的距离定义是其各坐标数值差的最大值。

国际象棋中，国王走一步能够移动到相邻的8个方格中的任意一个。那么国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？自己走走试试。
你会发现最少步数总是max( | x2-x1 | , | y2-y1 | ) 步 。这种距离度量方法叫切比雪夫距离。

案例：R模拟 f6（王）到c4的切比雪夫距离
a<-c(3,4)
b<-c(6,6)
dist(rbind(a,b),method=“maximum”)
a
b 3

即王到c4至少走3步。
综合案例

package com.yasuofenglei

object Driver04 {
  def main(args: Array[String]): Unit = {
    val a1=Array(1,2)
    val a2=Array(4,7)
    //计算出a1和a2之间的欧式距离
    //拉链方法：zip
    //开方方法Math.sqrt()
    val r1=a1.zip(a2).map(x => (x._1-x._2)*(x._1-x._2)).sum
    println(Math.sqrt(r1))
    
    //计算两点间的夹角余弦
    val a1a2Fenzi=a1.zip(a2).map{x => x._1*x._2}.sum
    val a1Fenmu =Math.sqrt(a1.map{x => x*x}.sum)
    val a2Fenmu =Math.sqrt(a2.map{x => x*x}.sum)
    
    val a1a2Cos=a1a2Fenzi/(a1Fenmu*a2Fenmu)
    println(a1a2Cos)
    
  }
}

最小二乘法

介绍
最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

背景故事
最小二乘法(Least Squares Method,简记为LSE)是一个比较古老的方法，源于天文学和测地学上的应用需要。在早期数理统计方法的发展中，这两门科学起了很大的作用。丹麦统计学家霍尔把它们称为“数理统计学的母亲”。此后近三百年来，它广泛应用于科学实验与工程技术中。美国统计史学家斯蒂格勒( S. M. Stigler)指出, 最小二乘方法是19世纪数理统计学的压倒一切的主题。1815年时,这方法已成为法国、意大利和普鲁士在天文和测地学中的标准工具,到1825年时已在英国普遍使用。

朱赛普·皮亚齐

追溯到1801年，意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。经过40天的跟踪观测后，由于谷神星运行至太阳背后，使得皮亚齐失去了谷神星的位置。随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星，但是根据大多数人计算的结果来寻找谷神星都没有结果。

时年24岁的高斯也计算了谷神星的轨道。奥地利天文学家海因里希·奥尔伯斯根据高斯计算出来的轨道重新发现了谷神星。高斯于其1809年的著作《关于绕日行星运动的理论》中。在此书中声称他自1799年以来就使用最小二乘方法,由此爆发了一场与勒让德的优先权之争。

近代学者经过对原始文献的研究,认为两人可能是独立发明了这个方法,但首先见于书面形式的，以勒让德为早。然而,现今教科书和著作中,多把这个发明权归功于高斯。其原因,除了高斯有更大的名气外,主要可能是因为其正态误差理论对这个方法的重要意义。勒让德在其著作中,对最小二乘方法的优点有所阐述。然而,缺少误差分析。我们不知道,使用这个方法引起的误差如何,就需建立一种误差分析理论。高斯于1823年在误差e1 ,… , en独立同分布的假定下,证明了最小二乘方法的一个最优性质: 在所有无偏的线性估计类中,最小二乘方法是其中方差最小的！

现行的最小二乘法是勒让德( A. M. Legendre)于1805年在其著作《计算慧星轨道的新方法》中提出的。它的主要思想就是选择未知参数，使得理论值与观测值之差的平方和达到最小：

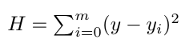
原理及推导过程
下面我们来看一下最简单的线性情况。
如下图所示，对于某个数据集(xi, yi) (i=0,1,…,n)，我们需要找到一条趋势线（图中的虚线），能够表达出数据集(xi, yi)这些点所指向的方向。



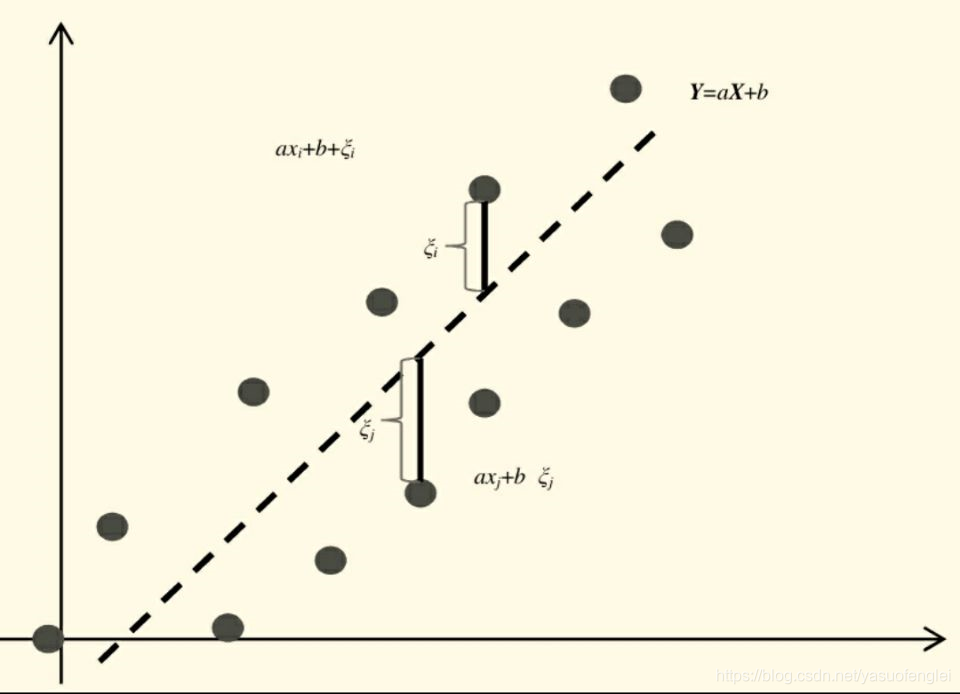
求解一组k和b，使得误差平方和最小（列差平方和RSS）得到对应的最优解。

建模相关的概念补充

• 建立目标方程去拟合样本数据，目标议程不固定。可以是线性方程，也可以是非线性方程。
• 求解目标方程的系数。目的是找出目标方程系数的最优解。所以需要找出目标方程的Cost Function（损失函数，代价方程）
• 通过损失函数得到最优解。
• 损失函数不固定，目标方程不同，损失函数也随之变化。

预测商品需求案例

lritem.txt

100|5 1000
75|7 600
80|6 1200
70|6 500
50|8 30
65|7 400
90|5 1300
100|4 1100
110|3 1300
60|9 300

针对预测商品需求案例，我们建立的是多元线性回归模型

• 回归模型是用于预测的，对于回归模型的种类：1最小二乘回归。2梯度下降回归。3岭回归。4Lasso回归。…
• 如果自变量只有一个，则是一元。如果自变量超过1个。都可以叫称为多元。
• 目标方程。直线方程，平面方程，超平面方程。线性议程的形式固定：比如直线方程y=β1X1+β0,平面方程Y=β1X1+β2X2+β0，超平面方程Y=β1X1+β2X2+…+βnXn+β0
• 目标议程也可以是一个非线性方程。非线性方程的形式不固定，不宜求解。

梯度下降法

最小二乘法法适用于模型方程存在解析解的情况。如果说一个函数不存在解析解，是不能用最小二乘法的，此时，只能通过数值解（迭代式的）去逼近真实解。

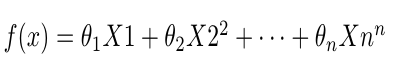
上面的方程就不存在解析解，每个系数无法用变量表达式表达。
梯度下降法要比最小二乘法的适用性更强

梯度下降法通过数值解（多次迭代），最后收敛于真实解。很多模型底层都是通过梯度下降法来求解系数。比如：逻辑回归模型，BP神经网络做误差反馈。 所以梯度下降法的应用比二乘法更广泛（因为二乘法只适用模型方程存在解析解的情况，而在生产环境下的模型议程较为复杂。很多都是不存在解析解的）
梯度从几何意义上，就是函数变化最快的方向，如果沿着梯度的正方向，可以以最快速度找到函数的最大值。
如果沿着梯度方向，可以最快速找到函数的极大值。->梯度上升法
如果沿着梯度负方向，可以最快速找到函数的极小值。->梯度下降法
我们常用的是梯度下降法，原因：
利用梯度下降法，找出损失函数的极小值(RSS)，得到main RSS对应的系数。
梯度下降法的算法过程：

1. 随机选取0的初始位置
2. 用步长（程序员自己定义）乘以损失函数的梯度，得到下降的距离，然后更新0。
3. 多次迭代第二步，直到收敛于损失函数的极小值（min RSS），从而得到最优解。
   上述过程，有两个关键要素：1步长，2损失函数的梯度。

package com.yasuofenglei.sgd

import org.apache.spark._
import org.apache.spark.sql.SQLContext
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.LinearRegressionWithSGD
/*
1,0 1
2,0 2
3,0 3
5,1 4
7,6 1
9,4 5
6,3 3
 */
object Driver {
  def main(args: Array[String]): Unit = {
    val conf = new SparkConf().setMaster("local").setAppName("sgd")
    val sc=new SparkContext(conf)
    
    val data=sc.textFile("d://data/ml/testSGD.txt")
    //1转换
    val parseData=data.map{line=>
      val info=line.split(",")
      val Y=info(0).toDouble
      val X1=info(1).split(" ")(0).toDouble
      val X2=info(1).split(" ")(1).toDouble
      LabeledPoint(Y,Vectors.dense(X1,X2))
    }
    //parseData.foreach{println}
    //建模，参数：迭代次数，步长
    //如果迭代次数过少，可能会导致还未收敛就结束了，误差很大。如果过多，会浪费CPU，导致计算代价过大
    //如果步长过小，会导致迭代很多次仍不收敛，如果过大，会导致围绕真实解来回震荡而不收敛
    //综上，建议：年代次数多一点，步长小一点（经验：0.05~0.5）
    val model=LinearRegressionWithSGD.train(parseData,20,0.05)
    
    //提取模型的自变量系数
    val coef=model.weights
    //通过模型实现预测
    //回代样本集预测，要求传入的数据类型RDD[Vector(X1,X2)]
    val predict=model.predict(parseData.map{x=> x.features})
    predict.foreach{println}
  }
}

梯度下降法的种类有三种

1. 批量梯度下降法-BGD
   每次更新系数时，是所有的样本都需要参与计算。
   优点是需要很少的年代次数就可以收敛。
   缺点是如果样本量很大，则迭代一次时间很长。
   生产环境一般不用此方法（因为数据量大）
2. 随机梯度下降法-SGD
   每次更新系数时，是从所有的样本中随机选取一个样本参与更新。
   优点每次更新系数用时很短
   缺点需要更多的迭代次数才能收敛。
   所以目前生产环境都是用这种来解系数。
3. 小批量梯度下降法
   这种算法相当于综合了上述两种，选取一小批数据参与样本更新。

逻辑回归模型

逻辑回归模型可以对离散型数据响应，所以这种模型应用于干分类问题。而之前学习线性回归模型，是对连续型数据响应，不能对离苏型数据响应。。
基本概念

• 连续型数据，给定一区间，可以取区间内任意一实数值
• 离散型数据，给定一区间，只能取区间内有限个的实数值。

Sigmoid函数

此函数的作用：可以将任意的一实数值，映射到0或1。把任意的一连续型数据离散化0或1。

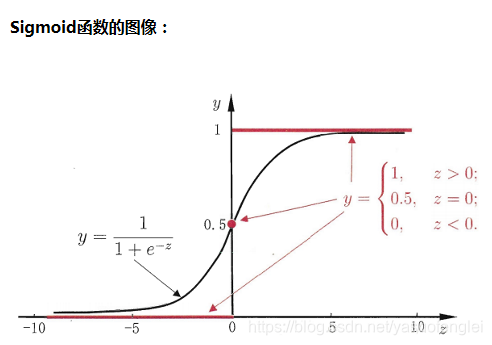
上图中，e是一个超越数，约等于2.718。e=(1+1/n)^n，当n趋近于无穷时，得到的值就是超越数。

package com.yasuofenglei.logistic

import org.apache.spark._
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.classification.LogisticRegressionWithSGD
import org.apache.spark.mllib.classification.LogisticRegressionWithLBFGS
/*
建立逻辑回归模型，应用场景：用于二分类问题
因变量（离散的，取值情况有两种，1or0）
 */
/*样本数据
17	1	1	1
44	0	0	1
48	1	0	1
55	0	0	1
75	1	1	1
35	0	1	0
42	1	1	0
57	0	0	0
28	0	1	0
20	0	1	0
38	1	0	0
45	0	1	0
47	1	1	0
52	0	0	0
55	0	1	0
68	1	0	1
18	1	0	1
68	0	0	1
48	1	1	1
17	0	0	1
 * */
object Driver {
  def main(args: Array[String]): Unit = {
    val conf= new SparkConf().setMaster("local").setAppName("logistic");
    val sc=new SparkContext(conf)
    val data=sc.textFile("d://data/ml/logistic.txt")
    //第一步，为了满足建模需要，需要做数据转换
    //RDD[String]->RDD[LabelPoint]
    val parseData=data.map{line => 
      val info=line.split("\t")
      val Y=info.last.toDouble;
      val featuresArray=info.take(3).map{_.toDouble};
      LabeledPoint(Y,Vectors.dense(featuresArray))
    }
    //parseData.foreach{println}
    //第二步建立逻辑回归模型,底层用的是随机梯度下降法来解出系数
//    val model= LogisticRegressionWithSGD.train(parseData, 500,1) //参数不好调
    //建立逻辑回归模型，底层用的是拟牛顿法来解出系数,
    /*这种算法通过数值解逼近真实解（迭代算法），属于快速迭代法，并且不需要指定步长
     * 优点：迭代次数少，而且不需要指定步长
     * 缺点：每迭代一次，计算量较大，所以如果数据量较大，还是建议使用SGD
     * */
    val model=new LogisticRegressionWithLBFGS().run(parseData) 
    //模型系数
    val coef=model.weights
    //第三步，回代样本，做预测（分类）
    val predict=model.predict(parseData.map{x=>x.features})
    predict.foreach{println}
    /*
     * 预测数据
18	0	0
35	1	1
40	0	1
22	1	0
     * */
    val testData=sc.textFile("d://data/ml/testLogistic.txt")
    val parseTestData=testData.map{line=>line.split("\t").map{num => num.toDouble}}
      .map{arr=>Vectors.dense(arr)}
      
    val testPredict=model.predict(parseTestData)
    testPredict.foreach { println}
  }
}