算法学习FFT系列(1):初习快速傅里叶变换
引入
这个坑已经在我脑海里占了很久了,但是一直没有水平写,今天尝试着写写看FFT的算法学习。
FFT在OI中最大的作用是加速卷积。理论上背板子是没毛病的,但是仍然遇到了一些考定义的毒瘤题,所以还是理解比较好。
多项式乘法
定义
多项式
多项式乘法就是
显然,多项式乘法需要 的复杂度。
表示方法
普通的多项式表示方法把n阶多项式
表示为向量
这里需要引入一种全新的表示方法——点值表示法。
也就是
表示为
n阶多项式和n个互不相同的点值表示一一对应。
这样的表示方法的优点是什么?考虑多项式乘法的过程。
转化成点值表示的两个式子,不难发现,其乘法复杂度是 的
FFT的总路线:系数表达式->点值表达式->乘法->点值表达式->系数表达式
插值(*)
这个东西是顺便一提,FFT中系数表达式<->点值表达式过程并不是FFT的专属,但是确是FFT的关键。这一过程被称之为插值。证明插值的唯一性(也就是n阶多项式和n个互不相同的点值表示一一对应。)需要通过范德蒙德矩阵的可逆性。
左边的矩阵表示为
就是范德蒙德矩阵
证明不会,自行百度。
插值相关还有这些东西,可以看看算法学习:拉格朗日插值
既然是点值表达式,最重要的就是带入什么点值,这里我们引入一个新的概念——单位复根。
单位复根
的表达式是
,更形象地,我们可以通过复数运算的几何意义(幅角相加, 模相乘)得到下面两张图
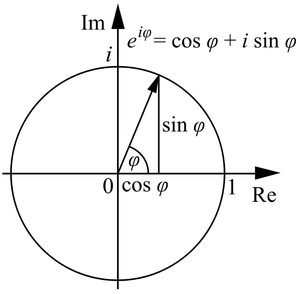
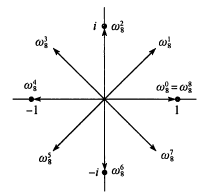
我们可以得到n次单位复根有n个,均匀分布在复平面上半径为1的圆上。
欧拉公式与单位复根表示
证明的方法是泰勒展开。
带入
得到
于是
其实
构成了一个乘法群。。。不加以赘述。
有了表达式,我们就可以挖掘
的性质了。
各种定理
消去引理
证明:
折半引理
如果 且n为偶数,那么n个n次单位复根的平方的集合就是 个 次单位复根的集合
证明:其实就是证明两个东西(1) (2) )
求和引理
证明:
特别地:
前置技能已经get得差不多了,开始表演
离散型傅里叶变换和逆离散型傅里叶变换(DFT和IDFT)
应该还记得快速傅里叶变换要干什么吧。
快速插值。
我们要做的事情就是
(1)
(2)
刚才介绍了这么多优秀的单位复根的性质,于是我们容易想到,把单位复根带入多项式里面。(为了方便,我们用
表示
)
假设序列
乘法之后得到的序列是
,其长度是
长度之和减一。我们找到一个最小n使得n大于C的长度并且n是2的整数次幂(为啥?之后会提到。)
我们可以把卷积变成这样的形式。
由求和引理可得
于是
刚才经过一波推导我们成功地找到了
点值表达式和
系数表达式的关系。
这样子的话问题转化为
(1)
(2)
前者即为DFT,后者即是IDFT
我们不难发现,两者的过程惊人的相似,其实只是多了
和一个-
于是我们使用同一个算法——快速傅里叶算法(FFT)来实现这玩意儿。
快速傅里叶变换(FFT)
设
注意到
这就是单位复根最英霸的地方,折半引理和消去引理可以使得它能够把插值的过程分治。上述操作被称为蝴蝶操作。
上文有提到,n是2的整数次幂,所以这个过程可以一直递推下去。不难发现,上述算法的时间复杂度递推式是。
由主定理可得时间复杂度为
IDFT有两种写法,第一种是老老实实地带一个负号进去,其实还有第二种写法。
我们把A数组反转一下,DFT之后除以n就好了。
代码实现
注意到
所以我们全程是用欧拉公式来表示
的
还有一点,蝴蝶操作本来我们是要迭代的,但是这里有一个优化常数的小技巧。
考虑原序列是
模拟蝴蝶变换的过程。
如果用二进制表示原序列和变换后的序列
原
后
发现其实就是二进制反转了。
然后我们就可以用递推写这个东西了,具体看代码吧。
//luoguP3803 【模板】多项式乘法(FFT)
//一个比较易于理解的版本,其实可以写得更简洁。
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int N = 5e6 + 10;
const double pi = acos(-1.0);
struct cp {
double r, i;
cp(double _r = 0, double _i = 0) : r(_r), i(_i) {}
cp operator + (cp a) {return cp(r + a.r, i + a.i);}
cp operator - (cp a) {return cp(r - a.r, i - a.i);}
cp operator * (double a) {return cp(r * a, i * a);}
cp operator * (cp a) {return cp(r * a.r - i * a.i, r * a.i + i * a.r);}
}a[N], b[N];
int r[N], m;
void FFT(cp *F, int f) {
for(int i = 0;i < m; ++i) if(i < r[i]) swap(F[i], F[r[i]]);
for(int i = 1; i < m; i <<= 1) {
cp wn(cos(pi / i), f * sin(pi / i));
for(int j = 0;j < m; j += (i << 1)) {
cp w(1, 0);
for(int l = 0;l < i; ++l, w = w * wn) {
cp x = F[j + l], y = w * F[j + i + l];
F[j + l] = x + y; F[j + i + l] = x - y;
}
}
}
if(!~f) for(int i = 0;i < m; ++i) F[i].r /= m;
}
int main() {
int n1, n2; scanf("%d%d", &n1, &n2);
for(int i = 0, x;i <= n1; ++i) scanf("%d", &x), a[i] = cp(x, 0);
for(int i = 0, x;i <= n2; ++i) scanf("%d", &x), b[i] = cp(x, 0);
int L = 0; for(m = 1; (m <<= 1) <= (n1 + n2); ++L) ;
for(int i = 1; i < m; ++i) r[i] = (r[i >> 1] >> 1) | (i & 1) << L;
FFT(a, 1); FFT(b, 1); for(int i = 0;i < m; ++i) a[i] = a[i] * b[i];
FFT(a, -1);
for(int i = 0;i <= n1 + n2; ++i) printf("%d ", (int)(a[i].r + 0.5)); puts("");
return 0;
}后记
参考博文
[学习笔记] 多项式与快速傅里叶变换(FFT)基础
Pick‘s Blog 里面有各种FFT系列的东西