LDPC码简介
低密度校验码(LDPC码)是一种前向纠错码,LDPC码最早在20世纪60年代由Gallager在他的博士论文中提出,但限于当时的技术条件,缺乏可行的译码算法,此后的35年间基本上被人们忽略,其间由Tanner在1981年推广了LDPC码并给出了LDPC码的图表示,即后来所称的Tanner图。1993年Berrou等人发现了Turbo码,在此基础上,1995年前后MacKay和Neal等人对LDPC码重新进行了研究,提出了可行的译码算法,从而进一步发现了LDPC码所具有的良好性能,迅速引起强烈反响和极大关注。经过十几年来的研究和发展,研究人员在各方面都取得了突破性的进展,LDPC码的相关技术也日趋成熟,甚至已经开始有了商业化的应用成果,并进入了无线通信等相关领域的标准。
-
LDPC码的特点
LDPC码是一种分组码,其校验矩阵只含有很少量非零元素。正是校验矩阵的这种稀疏性,保证了译码复杂度和最小码距都只随码长呈现线性增加。除了校验矩阵是稀疏矩阵外,码本身与任何其它的分组码并无二致。其实如果现有的分组码可以被稀疏矩阵所表达,那么用于码的迭代译码算法也可以成功的移植到它身上。然而,一般来说,为现有的分组码找到一个稀疏矩阵并不实际。不同的是,码的设计是以构造一个校验矩阵开始的,然后才通过它确定一个生成矩阵进行后续编码。而LDPC的编码就是本文所要讨论的主体内容。对于LDPC码而言,校验矩阵的选取十分关键,不仅影响LDPC码的纠错性能力,也影响LDPC编译码的复杂度及硬件实现的复杂度。准循环 LDPC 码(Quasi-Cycle,QC-LDPC)是 LDPC 码中重要的一类,是指一个码字以右移或左移固定位数的符号位得到的仍是一个码字。QC-LDPC 码的校验矩阵是由循环子矩阵的阵列组成,相对于其他类型的 LDPC 码,在编码和解码的硬件实现上具有许多优点。编码可以通过反馈移位寄存器有效实现,采用串行算法,编码的复杂度与校验比特位数成正比,而采用并行算法,编码复杂度与码字长度成正比。对硬件解码实现,准循环的结构简化了消息传递的路径,可以部分并行解码,实现了解码复杂度和速率的折中。这些优点,使得 QC-LDPC 码作为未来通信和存储系统应用的主要 LDPC 码。 -
译码算法的选择
译码方法是LDPC码与经典的分组码之间的最大区别。经典的分组码一般是用ML类的译码算法进行译码的,所以它们一般码长较小,并通过代数设计以减低译码工作的复杂度。但是LDPC码码长较长,并通过其校验矩阵H的图像表达而进行迭代译码,所以它的设计以校验矩阵的特性为核心考虑之一。由于 LDPC 码校验矩阵的稀疏性,其译码复杂度与码长不是指数关系,而是线性关系,因而 LDPC 码的码长可以很长,可以达到几千到几万甚至更高,这样带来的一个好处是:一个码字内各比特之间的关联长度比较长,一般通过迭代译码方法进行译码,充分利用码字内各比特的关联性以提高译码准确度,并且还充分利用了信道的特征。本课题采用的译码算法为置信传播(BP)译码算法,置信传播算法是基于 Tanner 图的迭代译码算法。在迭代过程中,可靠性信息,即“消息”通过 Tanner图上的边在变量节点和校验节点中来回传递,经多次迭代后趋于稳定值,然后据此进行最佳判决,BP译码算法有着非常好译码性能。 -
Tanner图
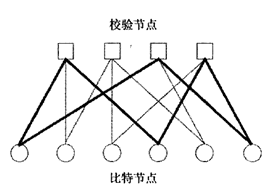
LDPC码常常通过图来表示,而Tanner图所表示的其实是LDPC码的校验矩阵。Tanner图包含两类顶点:n个码字比特顶点(称为比特节点),分别与校验矩阵的各列相对应和m个校验方程顶点(称为校验节点),分别与校验矩阵的各行对应。校验矩阵的每行代表一个校验方程,每列代表一个码字比特。所以,如果一个码字比特包含在相应的校验方程中,那么就用一条连线将所涉及的比特节点和校验节点连起来,所以Tanner图中的连线数与校验矩阵中的1的个数相同。以下图是矩阵的Tanner图,其中比特节点用圆形节点表示,校验节点用方形节点表示,加黑线显示的是一个6循环:

Tanner图中的循环是由图中的一群相互连接在一起的顶点所组成的,循环以这群顶点中的一个同时作为起点和终点,且只经过每个顶点一次。循环的长度定义为它所包含的连线的数量,而图形的围长,也可叫做图形的尺寸,定义为图中最小的循环长度。如上图中,图形的尺寸,即围长为6,如加黑线所示。
LDPC编码
- 基于校验矩阵H直接编码方案
首先推导出根据校验矩阵直接编码的等式。将尺寸为(m,n)校验矩阵写成如下形式:
Kij是校正因子,使每次计算出的
LDPC码简介
低密度校验码(LDPC码)是一种前向纠错码,LDPC码最早在20世纪60年代由Gallager在他的博士论文中提出,但限于当时的技术条件,缺乏可行的译码算法,此后的35年间基本上被人们忽略,其间由Tanner在1981年推广了LDPC码并给出了LDPC码的图表示,即后来所称的Tanner图。1993年Berrou等人发现了Turbo码,在此基础上,1995年前后MacKay和Neal等人对LDPC码重新进行了研究,提出了可行的译码算法,从而进一步发现了LDPC码所具有的良好性能,迅速引起强烈反响和极大关注。经过十几年来的研究和发展,研究人员在各方面都取得了突破性的进展,LDPC码的相关技术也日趋成熟,甚至已经开始有了商业化的应用成果,并进入了无线通信等相关领域的标准。
-
LDPC码的特点
LDPC码是一种分组码,其校验矩阵只含有很少量非零元素。正是校验矩阵的这种稀疏性,保证了译码复杂度和最小码距都只随码长呈现线性增加。除了校验矩阵是稀疏矩阵外,码本身与任何其它的分组码并无二致。其实如果现有的分组码可以被稀疏矩阵所表达,那么用于码的迭代译码算法也可以成功的移植到它身上。然而,一般来说,为现有的分组码找到一个稀疏矩阵并不实际。不同的是,码的设计是以构造一个校验矩阵开始的,然后才通过它确定一个生成矩阵进行后续编码。而LDPC的编码就是本文所要讨论的主体内容。对于LDPC码而言,校验矩阵的选取十分关键,不仅影响LDPC码的纠错性能力,也影响LDPC编译码的复杂度及硬件实现的复杂度。准循环 LDPC 码(Quasi-Cycle,QC-LDPC)是 LDPC 码中重要的一类,是指一个码字以右移或左移固定位数的符号位得到的仍是一个码字。QC-LDPC 码的校验矩阵是由循环子矩阵的阵列组成,相对于其他类型的 LDPC 码,在编码和解码的硬件实现上具有许多优点。编码可以通过反馈移位寄存器有效实现,采用串行算法,编码的复杂度与校验比特位数成正比,而采用并行算法,编码复杂度与码字长度成正比。对硬件解码实现,准循环的结构简化了消息传递的路径,可以部分并行解码,实现了解码复杂度和速率的折中。这些优点,使得 QC-LDPC 码作为未来通信和存储系统应用的主要 LDPC 码。 -
译码算法的选择
译码方法是LDPC码与经典的分组码之间的最大区别。经典的分组码一般是用ML类的译码算法进行译码的,所以它们一般码长较小,并通过代数设计以减低译码工作的复杂度。但是LDPC码码长较长,并通过其校验矩阵H的图像表达而进行迭代译码,所以它的设计以校验矩阵的特性为核心考虑之一。由于 LDPC 码校验矩阵的稀疏性,其译码复杂度与码长不是指数关系,而是线性关系,因而 LDPC 码的码长可以很长,可以达到几千到几万甚至更高,这样带来的一个好处是:一个码字内各比特之间的关联长度比较长,一般通过迭代译码方法进行译码,充分利用码字内各比特的关联性以提高译码准确度,并且还充分利用了信道的特征。本课题采用的译码算法为置信传播(BP)译码算法,置信传播算法是基于 Tanner 图的迭代译码算法。在迭代过程中,可靠性信息,即“消息”通过 Tanner图上的边在变量节点和校验节点中来回传递,经多次迭代后趋于稳定值,然后据此进行最佳判决,BP译码算法有着非常好译码性能。 -
Tanner图
LDPC码常常通过图来表示,而Tanner图所表示的其实是LDPC码的校验矩阵。Tanner图包含两类顶点:n个码字比特顶点(称为比特节点),分别与校验矩阵的各列相对应和m个校验方程顶点(称为校验节点),分别与校验矩阵的各行对应。校验矩阵的每行代表一个校验方程,每列代表一个码字比特。所以,如果一个码字比特包含在相应的校验方程中,那么就用一条连线将所涉及的比特节点和校验节点连起来,所以Tanner图中的连线数与校验矩阵中的1的个数相同。以下图是矩阵的Tanner图,其中比特节点用圆形节点表示,校验节点用方形节点表示,加黑线显示的是一个6循环:

Tanner图中的循环是由图中的一群相互连接在一起的顶点所组成的,循环以这群顶点中的一个同时作为起点和终点,且只经过每个顶点一次。循环的长度定义为它所包含的连线的数量,而图形的围长,也可叫做图形的尺寸,定义为图中最小的循环长度。如上图中,图形的尺寸,即围长为6,如加黑线所示。

LDPC编码
- 基于校验矩阵H直接编码方案
首先推导出根据校验矩阵直接编码的等式。将尺寸为(m,n)校验矩阵写成如下形式:
Kij是校正因子,使每次计算出的