Hamilton函数方法是变分法应用在控制系统上的标准化方法,即使不懂变分法,简单套用表格中的公式也可以列写出方程,这个方法是最优控制理论用的最多的方法。
按照第一章最优控制理论 一、变分法和泛函极值问题 ,我们已经讨论了有动力学方程约束
f
(
x
,
x
˙
,
t
)
=
0
f(x,\dot x,t)=0
f ( x , x ˙ , t ) = 0
H
x
−
d
d
t
H
x
˙
=
0
f
(
x
(
t
)
,
x
˙
(
t
)
,
t
)
=
0
\begin{aligned}H_x-\frac{\text d}{\text d t}H_{\dot x}=0\\ \mathbf f(\mathbf x(t),\dot \mathbf x(t),t)=0 \end{aligned}
H x − d t d H x ˙ = 0 f ( x ( t ) , x ˙ ( t ) , t ) = 0
其中的Hamilton函数
H
(
x
,
x
˙
,
λ
,
t
)
=
L
(
x
,
x
˙
,
t
)
−
λ
T
f
(
x
,
x
˙
,
t
)
H(x,\dot x,\lambda,t)=L(x,\dot x,t)-\lambda^{\mathrm T}f(x,\dot x,t)
H ( x , x ˙ , λ , t ) = L ( x , x ˙ , t ) − λ T f ( x , x ˙ , t )
t
f
t_f
t f
x
˙
=
f
[
x
(
t
)
,
u
(
t
)
,
t
]
;
x
(
t
o
)
=
x
0
t
o
≤
t
≤
t
f
min
u
(
t
)
J
=
φ
[
x
(
t
f
)
,
t
f
]
+
∫
t
o
t
f
L
[
x
(
t
)
,
u
(
t
)
,
t
]
d
t
(1)
\dot{x}=f[x(t), u(t), t] ; \quad x\left(t_{o}\right)=x_0\quad t_{o} \leq t \leq t_{f}\\ \min_{u(t)}J=\varphi\left[x\left(t_{f}\right), t_{f}\right]+\int_{t_{o}}^{t_{f}} L[x(t), u(t), t] d t \tag 1
x ˙ = f [ x ( t ) , u ( t ) , t ] ; x ( t o ) = x 0 t o ≤ t ≤ t f u ( t ) min J = φ [ x ( t f ) , t f ] + ∫ t o t f L [ x ( t ) , u ( t ) , t ] d t ( 1 )
式中包括了控制项
u
(
t
)
u(t)
u ( t )
J
[
x
(
t
)
,
x
˙
(
t
)
,
u
(
t
)
,
t
]
=
φ
(
0
)
+
∫
t
t
f
{
L
+
λ
T
[
f
(
x
,
u
,
t
)
−
x
˙
]
+
d
φ
(
x
,
t
)
d
t
}
d
t
=
φ
(
0
)
+
∫
t
t
f
H
ˉ
(
x
,
x
˙
,
λ
,
u
,
t
)
d
t
(†)
J[x(t),\dot x(t),u(t),t]=\varphi(0)+\int_{t}^{t_{f}}\left\{L+\lambda^{\mathrm T}[f(x, u, t)-\dot{x}]+\frac{\text d\varphi(x, t)}{\text d t}\right\} d t\\ =\varphi(0)+\int_{t}^{t_{f}}\bar H(x,\dot x,\lambda,u,t)\text d t\tag{\dag}
J [ x ( t ) , x ˙ ( t ) , u ( t ) , t ] = φ ( 0 ) + ∫ t t f { L + λ T [ f ( x , u , t ) − x ˙ ] + d t d φ ( x , t ) } d t = φ ( 0 ) + ∫ t t f H ˉ ( x , x ˙ , λ , u , t ) d t ( † )
对
x
(
t
)
x(t)
x ( t )
u
(
t
)
u(t)
u ( t )
λ
(
t
)
\lambda(t)
λ ( t )
H
ˉ
x
−
d
d
t
H
ˉ
x
˙
=
0
\bar H_x-\frac{\text d}{\text d t}\bar H_{\dot x}=0
H ˉ x − d t d H ˉ x ˙ = 0
H
ˉ
u
=
0
\bar H_u=0
H ˉ u = 0
H
ˉ
λ
=
0
\bar H_\lambda=0
H ˉ λ = 0
∂
L
∂
x
+
∂
f
T
∂
x
λ
(
t
)
+
λ
˙
(
t
)
=
0
f
(
x
,
u
,
t
)
−
x
˙
=
0
∂
L
∂
u
+
∂
f
T
∂
u
λ
λ
(
t
)
=
0
\begin{aligned} \frac{\partial L}{\partial x}+\frac{\partial f^{\mathrm{T}}}{\partial x} \lambda(t)+\dot{\lambda}(t)=0 \\ f(x,u,t)-\dot x=0\\ \frac{\partial L}{\partial u}+\frac{\partial f^{\mathrm{T}}}{\partial u^{\lambda}} \lambda(t)=0 \end{aligned}
∂ x ∂ L + ∂ x ∂ f T λ ( t ) + λ ˙ ( t ) = 0 f ( x , u , t ) − x ˙ = 0 ∂ u ∂ L + ∂ u λ ∂ f T λ ( t ) = 0
此外还有状态方程和边界条件:终端固定
x
(
t
f
)
=
x
f
x(t_f)=x_f
x ( t f ) = x f
H
ˉ
x
˙
(
t
f
)
=
0
\bar H_{\dot x}(t_f)=0
H ˉ x ˙ ( t f ) = 0
上面这个方程的形式不是很好,我们重新定义一个哈密尔顿函数:
H
[
x
(
t
)
,
u
(
t
)
,
λ
(
t
)
,
t
]
≜
L
[
x
(
t
)
,
u
(
t
)
,
t
]
+
λ
T
(
t
)
f
[
x
(
t
)
,
u
(
t
)
,
t
]
(2)
H[x(t), u(t), \lambda(t), t]\triangleq L[x(t), u(t), t]+\lambda^{\mathrm T}(t) f[x(t), u(t), t] \tag 2
H [ x ( t ) , u ( t ) , λ ( t ) , t ] ≜ L [ x ( t ) , u ( t ) , t ] + λ T ( t ) f [ x ( t ) , u ( t ) , t ] ( 2 )
那么性能指标化为:
J
[
x
(
t
)
,
x
˙
(
t
)
,
u
(
t
)
,
t
]
=
φ
(
0
)
−
λ
T
x
∣
0
t
f
+
∫
t
o
t
f
(
H
+
λ
˙
T
x
)
d
t
\begin{aligned} J[x(t),\dot x(t),u(t),t] &=\varphi(0)-\lambda^{\mathrm T} x\big|_0^{t_f} &+\int_{t_{o}}^{t_{f}}(H+\dot{\lambda}^{\mathrm T} x) d t \end{aligned}
J [ x ( t ) , x ˙ ( t ) , u ( t ) , t ] = φ ( 0 ) − λ T x ∣ ∣ 0 t f + ∫ t o t f ( H + λ ˙ T x ) d t
此时,Euler方程变为
λ
˙
=
−
∂
H
∂
x
=
−
∂
L
∂
x
−
λ
T
∂
f
∂
x
x
˙
=
∂
H
∂
λ
=
f
(
x
,
u
,
t
)
0
=
∂
H
∂
u
=
∂
L
∂
u
+
(
∂
f
∂
u
)
T
λ
(3)
\begin{aligned} \dot{\lambda}&=-\frac{\partial H}{\partial x}=-\frac{\partial L}{\partial x}-\lambda^{\mathrm T}\frac{\partial f}{\partial x}\tag{3}\\ \dot{x}&=\frac{\partial H}{\partial\lambda}=f(x,u,t)\\ 0&=\frac{\partial H}{\partial u}=\frac{\partial L}{\partial u}+\left(\frac{\partial f}{\partial u}\right)^{\mathrm T} \lambda \end{aligned}
λ ˙ x ˙ 0 = − ∂ x ∂ H = − ∂ x ∂ L − λ T ∂ x ∂ f = ∂ λ ∂ H = f ( x , u , t ) = ∂ u ∂ H = ∂ u ∂ L + ( ∂ u ∂ f ) T λ ( 3 )
这样,最优控制问题被规范化为3个Euler方程,按公式
(
3
)
(3)
( 3 )
(
1
)
−
(
3
)
(1)-(3)
( 1 ) − ( 3 )
首先写出性能指标
J
=
L
+
λ
T
f
J=L+\lambda^Tf
J = L + λ T f
依次列写协态方程
λ
˙
=
−
∂
H
∂
x
\dot\lambda=-\frac{\partial H}{\partial x}
λ ˙ = − ∂ x ∂ H
∂
H
∂
u
=
0
\frac{\partial H}{\partial u}=0
∂ u ∂ H = 0
将最优控制代入状态方程
x
˙
=
f
(
x
,
u
,
t
)
\dot x=f(x,u,t)
x ˙ = f ( x , u , t )
写出边界条件和横截条件如
x
(
t
f
)
,
λ
(
t
f
)
,
H
(
∗
,
t
f
)
x(t_f),\lambda(t_f),H(*,t_f)
x ( t f ) , λ ( t f ) , H ( ∗ , t f )
求解整个Hamilton系统
这个方法在通用性很强,可以解决大多数无约束问题、以及带有终端约束的最优控制问题。
除了Euler方程,还要考虑边界条件和定解条件才能实际求解。
x
(
t
)
,
λ
(
t
)
∈
R
n
,
u
(
t
)
∈
R
q
x(t),\lambda(t)\in \Reals^n,u(t)\in\Reals^q
x ( t ) , λ ( t ) ∈ R n , u ( t ) ∈ R q
2
n
+
q
2n+q
2 n + q
x
(
t
)
,
λ
(
t
)
x(t),\lambda(t)
x ( t ) , λ ( t )
2
n
2n
2 n
u
(
t
)
u(t)
u ( t )
x
(
t
)
x(t)
x ( t )
λ
(
t
)
\lambda(t)
λ ( t )
问题描述
未知变量个数
边界条件
横截条件
t
f
,
x
f
t_f,x_f
t f , x f
2
n
2n
2 n
x
(
t
0
)
=
x
0
,
x
(
t
f
)
=
x
f
x(t_0)=x_0,x(t_f)=x_f
x ( t 0 ) = x 0 , x ( t f ) = x f \
t
f
t_f
t f
x
f
x_f
x f
2
n
2n
2 n
x
(
t
0
)
=
x
0
x(t_0)=x_0
x ( t 0 ) = x 0
λ
(
t
f
)
=
∂
φ
(
⋅
∗
,
t
f
)
∂
x
\lambda(t_f)=\frac{\partial \varphi(\cdot^*,t_f)}{\partial x}
λ ( t f ) = ∂ x ∂ φ ( ⋅ ∗ , t f )
t
f
t_f
t f
x
f
x_f
x f
2
n
+
1
2n+1
2 n + 1
x
(
t
0
)
=
x
0
,
x
(
t
f
)
=
x
f
x(t_0)=x_0,x(t_f)=x_f
x ( t 0 ) = x 0 , x ( t f ) = x f
H
(
⋅
∗
,
t
f
)
+
∂
φ
(
⋅
∗
,
t
f
)
∂
t
=
0
H(\cdot^*,t_f)+\frac{\partial \varphi(\cdot^*,t_f)}{\partial t}=0
H ( ⋅ ∗ , t f ) + ∂ t ∂ φ ( ⋅ ∗ , t f ) = 0
t
f
,
x
f
t_f,x_f
t f , x f
2
n
+
1
2n+1
2 n + 1
x
(
t
0
)
=
x
0
x(t_0)=x_0
x ( t 0 ) = x 0
λ
(
t
f
)
=
∂
φ
∂
x
;
H
(
⋅
∗
,
t
f
)
+
∂
φ
(
⋅
∗
,
t
f
)
∂
t
=
0
\lambda(t_f)=\frac{\partial \varphi}{\partial x};\\H(\cdot^*,t_f)+\frac{\partial \varphi(\cdot^*,t_f)}{\partial t}=0
λ ( t f ) = ∂ x ∂ φ ; H ( ⋅ ∗ , t f ) + ∂ t ∂ φ ( ⋅ ∗ , t f ) = 0
上面,性能指标不包括Meyer型,即
φ
(
x
(
t
f
)
,
t
f
)
)
≡
0
\varphi(x(t_f),t_f))\equiv0
φ ( x ( t f ) , t f ) ) ≡ 0
t
f
,
x
f
t_f,x_f
t f , x f
λ
(
t
f
)
=
0
,
H
(
⋅
∗
,
t
f
)
=
0
\lambda(t_f)=0,H(\cdot^*,t_f)=0
λ ( t f ) = 0 , H ( ⋅ ∗ , t f ) = 0
设终端时刻
t
f
t_f
t f
x
f
x_f
x f
ψ
(
x
f
,
t
f
)
=
0
,
ψ
∈
R
m
,
m
<
n
(5)
\psi(x_f,t_f)=0,\psi\in\Reals^m,m\lt n\tag 5
ψ ( x f , t f ) = 0 , ψ ∈ R m , m < n ( 5 )
(
1
)
(1)
( 1 )
x
f
x_f
x f
x
i
(
t
f
)
=
x
i
f
,
i
=
1
,
2
,
…
,
m
<
n
x_i(t_f)=x_{if},i=1,2,\dots,m<n
x i ( t f ) = x i f , i = 1 , 2 , … , m < n
x
f
x_f
x f
r
f
⋅
v
f
=
0
\mathbf r_f\cdot\mathbf v_f=0
r f ⋅ v f = 0
参考文献[2],按照Lagrange乘数法,设一个常数向量
μ
∈
R
m
\mu\in\Reals^{m}
μ ∈ R m
J
=
[
φ
+
μ
T
ψ
]
t
f
+
∫
0
t
f
{
L
(
x
,
u
,
t
)
+
λ
T
[
f
(
x
,
u
,
t
)
−
x
˙
]
}
d
t
=
Φ
t
f
+
∫
0
t
f
(
H
−
λ
T
x
˙
)
d
t
\begin{aligned} J&=\left[\varphi+\mu^{\mathrm T} \psi\right]_{t_{f}}+\int_{0}^{t_{f}}\left\{L(x, u, t)+\lambda^{\mathrm T}[f(x, u, t)-\dot{x}]\right\} d t\\ &=\Phi_{t_f}+\int_{0}^{t_{f}}(H-\lambda^{\mathrm T}\dot x)dt \end{aligned}
J = [ φ + μ T ψ ] t f + ∫ 0 t f { L ( x , u , t ) + λ T [ f ( x , u , t ) − x ˙ ] } d t = Φ t f + ∫ 0 t f ( H − λ T x ˙ ) d t
上式仍然定义相同的Hamilton函数
H
≜
L
+
λ
T
f
H\triangleq L+\lambda^{\mathrm T}f
H ≜ L + λ T f
Φ
(
x
(
t
f
)
,
t
f
)
≜
φ
+
μ
T
ψ
(‡)
\Phi(\mathbf x(t_f),t_f)\triangleq \varphi+\mu^{\mathrm T} \psi\tag\ddag
Φ ( x ( t f ) , t f ) ≜ φ + μ T ψ ( ‡ )
d
J
=
(
(
∂
Φ
∂
t
+
L
)
d
t
+
∂
Φ
∂
x
d
x
)
t
f
+
∫
0
t
f
(
∂
H
∂
x
δ
x
+
∂
H
∂
u
δ
u
−
λ
T
δ
x
˙
)
d
t
\begin{aligned} d J=\left(\left(\frac{\partial \Phi}{\partial t}+L\right) d t+\frac{\partial \Phi}{\partial x} d x\right) _{t_f} &+\int_{0}^{t_{f}}\left(\frac{\partial H}{\partial x} \delta x+\frac{\partial H}{\partial u} \delta u-\lambda^{\mathrm T} \delta \dot{x}\right) d t \end{aligned}
d J = ( ( ∂ t ∂ Φ + L ) d t + ∂ x ∂ Φ d x ) t f + ∫ 0 t f ( ∂ x ∂ H δ x + ∂ u ∂ H δ u − λ T δ x ˙ ) d t
并考虑
δ
x
(
t
)
=
d
x
(
t
)
−
x
˙
(
t
)
d
t
\delta x(t)=\text d x(t)-\dot x(t)\text d t
δ x ( t ) = d x ( t ) − x ˙ ( t ) d t
d
J
=
(
∂
Φ
∂
t
+
L
+
λ
T
x
˙
)
t
f
d
t
f
+
[
(
∂
Φ
∂
x
−
λ
T
)
d
x
]
t
f
+
(
λ
T
δ
x
)
t
0
+
∫
0
t
f
[
(
∂
H
∂
x
+
λ
˙
T
)
δ
x
+
∂
H
∂
u
δ
u
]
d
t
(6)
\text d J=\left(\frac{\partial \Phi}{\partial t}+L+\lambda^{\mathrm T} \dot{x}\right)_{t_{f}}\text d t_{f}+\left[\left(\frac{\partial \Phi}{\partial x}-\lambda^{\mathrm T}\right)\text d x\right]_{t_{f}}+\\\left(\lambda^{\mathrm T} \delta x\right)_{t_0} +\int_{0}^{t_{f}}\left[\left(\frac{\partial H}{\partial x}+\dot{\lambda}^{\mathrm T}\right) \delta x+\frac{\partial H}{\partial u} \delta u\right]\text d t \tag 6
d J = ( ∂ t ∂ Φ + L + λ T x ˙ ) t f d t f + [ ( ∂ x ∂ Φ − λ T ) d x ] t f + ( λ T δ x ) t 0 + ∫ 0 t f [ ( ∂ x ∂ H + λ ˙ T ) δ x + ∂ u ∂ H δ u ] d t ( 6 )
按照最优性的必要条件,令每一项的系数都为0,可以得到Euler方程
λ
˙
=
−
∂
H
∂
x
=
−
∂
L
∂
x
−
λ
T
∂
f
∂
x
x
˙
=
f
(
x
,
u
,
t
)
0
=
∂
H
∂
u
=
∂
L
∂
u
+
(
∂
f
∂
u
)
T
λ
(7)
\begin{aligned} \dot{\lambda}&=-\frac{\partial H}{\partial x}=-\frac{\partial L}{\partial x}-\lambda^{\mathrm T}\frac{\partial f}{\partial x}\\ \dot{x}&=f(x,u,t)\\ 0&=\frac{\partial H}{\partial u}=\frac{\partial L}{\partial u}+\left(\frac{\partial f}{\partial u}\right)^{\mathrm T} \lambda \end{aligned}\tag{7}
λ ˙ x ˙ 0 = − ∂ x ∂ H = − ∂ x ∂ L − λ T ∂ x ∂ f = f ( x , u , t ) = ∂ u ∂ H = ∂ u ∂ L + ( ∂ u ∂ f ) T λ ( 7 )
边界条件和横截条件
λ
T
(
t
f
)
=
∂
Φ
(
⋅
∗
,
t
f
)
∂
x
=
∂
φ
(
x
f
,
t
f
)
∂
x
+
μ
T
∂
ψ
(
x
f
,
t
f
)
∂
x
(
∂
Φ
∂
t
+
λ
T
x
˙
+
L
)
t
=
t
f
≡
(
d
Φ
d
t
+
L
)
t
=
t
f
=
0
(8)
\begin{aligned} \lambda^{\mathrm T}\left(t_{f}\right)=\frac{\partial \Phi(\cdot^*,t_f)}{\partial x}=\frac{\partial \varphi(x_f,t_f)}{\partial x}+\mu^{\mathrm T} \frac{\partial \psi(x_f,t_f)}{\partial x} \\ \left(\frac{\partial \Phi}{\partial t}+\lambda^{\mathrm T} \dot{x}+L\right)_{t=t_{f}}\equiv \left(\frac{\text d \Phi}{\text d t}+L\right)_{t=t_{f}}=0 \end{aligned}\tag{8}
λ T ( t f ) = ∂ x ∂ Φ ( ⋅ ∗ , t f ) = ∂ x ∂ φ ( x f , t f ) + μ T ∂ x ∂ ψ ( x f , t f ) ( ∂ t ∂ Φ + λ T x ˙ + L ) t = t f ≡ ( d t d Φ + L ) t = t f = 0 ( 8 )
可见文献[2]按照公式
(
6
)
(6)
( 6 ) 实际上,方程
(
6
)
(6)
( 6 ) 。其中
x
(
t
)
,
λ
(
t
)
x(t),\lambda(t)
x ( t ) , λ ( t )
μ
\mu
μ
问题描述
未知变量个数
边界条件
横截条件
t
f
t_f
t f
x
f
x_f
x f
ψ
(
x
f
,
t
f
)
=
0
\psi(x_f,t_f)=0
ψ ( x f , t f ) = 0
2
n
+
m
2n+m
2 n + m
x
(
t
0
)
=
x
0
ψ
(
x
f
,
t
f
)
=
0
x(t_0)=x_0\\ \psi(x_f,t_f)=0
x ( t 0 ) = x 0 ψ ( x f , t f ) = 0
λ
(
t
f
)
=
∂
Φ
∂
x
≡
∂
φ
∂
x
+
μ
T
∂
ψ
∂
x
\lambda(t_f)=\frac{\partial \Phi}{\partial x}\equiv\frac{\partial \varphi}{\partial x}+\mu^{\mathrm T}\frac{\partial\psi}{\partial x}
λ ( t f ) = ∂ x ∂ Φ ≡ ∂ x ∂ φ + μ T ∂ x ∂ ψ
t
f
t_f
t f
x
f
x_f
x f
ψ
(
x
f
,
t
f
)
=
0
\psi(x_f,t_f)=0
ψ ( x f , t f ) = 0
2
n
+
m
2n+m
2 n + m
x
(
t
0
)
=
x
0
ψ
(
x
f
,
t
f
)
=
0
x(t_0)=x_0\\ \psi(x_f,t_f)=0
x ( t 0 ) = x 0 ψ ( x f , t f ) = 0
λ
(
t
f
)
=
μ
T
∂
ψ
∂
x
\lambda(t_f)=\mu^{\mathrm T}\frac{\partial\psi}{\partial x}
λ ( t f ) = μ T ∂ x ∂ ψ
t
f
,
x
f
t_f,x_f
t f , x f
ψ
(
x
f
,
t
f
)
=
0
\psi(x_f,t_f)=0
ψ ( x f , t f ) = 0
2
n
+
m
+
1
2n+m+1
2 n + m + 1
x
(
t
0
)
=
x
0
ψ
(
x
f
,
t
f
)
=
0
x(t_0)=x_0\\ \psi(x_f,t_f)=0
x ( t 0 ) = x 0 ψ ( x f , t f ) = 0
λ
(
t
f
)
=
∂
Φ
∂
x
≡
∂
φ
∂
x
+
μ
T
∂
ψ
∂
x
;
∂
φ
∂
t
+
μ
T
∂
ψ
∂
t
+
(
∂
φ
∂
x
+
μ
T
∂
ψ
∂
x
)
f
+
L
=
0
,
(
t
=
t
f
)
\lambda(t_f)=\frac{\partial \Phi}{\partial x}\equiv\frac{\partial \varphi}{\partial x}+\mu^{\mathrm T}\frac{\partial\psi}{\partial x};\\ \frac{\partial \varphi}{\partial t}+\mu^{\mathrm T} \frac{\partial \psi}{\partial t}+\left(\frac{\partial \varphi}{\partial x}+\mu^{\mathrm T} \frac{\partial \psi}{\partial x}\right) f+L=0,(t=t_{f})
λ ( t f ) = ∂ x ∂ Φ ≡ ∂ x ∂ φ + μ T ∂ x ∂ ψ ; ∂ t ∂ φ + μ T ∂ t ∂ ψ + ( ∂ x ∂ φ + μ T ∂ x ∂ ψ ) f + L = 0 , ( t = t f )
t
f
,
x
f
t_f,x_f
t f , x f
ψ
(
x
f
,
t
f
)
=
0
\psi(x_f,t_f)=0
ψ ( x f , t f ) = 0
2
n
+
m
+
1
2n+m+1
2 n + m + 1
x
(
t
0
)
=
x
0
ψ
(
x
f
,
t
f
)
=
0
x(t_0)=x_0\\ \psi(x_f,t_f)=0
x ( t 0 ) = x 0 ψ ( x f , t f ) = 0
λ
(
t
f
)
=
∂
φ
∂
x
+
μ
T
∂
ψ
∂
x
;
μ
T
[
∂
ψ
∂
t
+
∂
ψ
∂
x
f
]
+
L
=
0
,
(
t
=
t
f
)
\lambda(t_f)=\frac{\partial \varphi}{\partial x}+\mu^{\mathrm T}\frac{\partial\psi}{\partial x};\\ \mu^{\mathrm T} [\frac{\partial \psi}{\partial t}+ \frac{\partial \psi}{\partial x} f]+L=0,(t=t_{f})
λ ( t f ) = ∂ x ∂ φ + μ T ∂ x ∂ ψ ; μ T [ ∂ t ∂ ψ + ∂ x ∂ ψ f ] + L = 0 , ( t = t f )
上表中的标量函数
Φ
(
x
(
t
f
)
,
t
f
)
\Phi(x(t_f),t_f)
Φ ( x ( t f ) , t f )
(
‡
)
(\ddag)
( ‡ )
倒立摆按照方程
I
θ
¨
+
b
θ
˙
−
m
g
l
sin
θ
=
u
I\ddot\theta+b\dot\theta-mgl\sin\theta=u
I θ ¨ + b θ ˙ − m g l sin θ = u
x
0
=
[
θ
,
ω
]
T
=
[
π
,
0
]
x_0=[\theta,\omega]^{\mathrm T}=[\pi,0]
x 0 = [ θ , ω ] T = [ π , 0 ]
[
θ
f
,
ω
f
]
T
=
[
0
,
0
]
[\theta_f,\omega_f]^{\mathrm T}=[0,0]
[ θ f , ω f ] T = [ 0 , 0 ]
t
f
t_f
t f
min
u
(
t
)
=
1
2
x
f
T
Q
x
f
+
1
2
∫
0
t
f
R
u
2
\min_{u(t)}=\frac1 2\mathbf x_f^{\mathrm T}\text Q\mathbf x_f+\frac1 2\int_0^{t_f}\text R\mathbf u^2
u ( t ) min = 2 1 x f T Q x f + 2 1 ∫ 0 t f R u 2
[
θ
˙
ω
˙
]
=
f
(
x
)
=
[
ω
1
/
I
(
−
m
g
l
sin
θ
+
b
ω
+
u
)
]
\begin{bmatrix}\dot\theta\\\dot\omega\end{bmatrix}=\mathbf f(\mathbf x)=\begin{bmatrix}\omega\\1/I(-mgl\sin\theta+b\omega+u)\end{bmatrix}
[ θ ˙ ω ˙ ] = f ( x ) = [ ω 1 / I ( − m g l sin θ + b ω + u ) ]
写出Hamilton函数
H
=
1
2
R
u
2
+
λ
1
ω
+
λ
2
ω
˙
H=\frac1 2\text R u^2+\lambda_1\omega+\lambda_2\dot\omega
H = 2 1 R u 2 + λ 1 ω + λ 2 ω ˙
协态方程
λ
˙
1
=
−
∂
H
∂
θ
=
λ
2
m
g
l
cos
θ
/
I
λ
˙
2
=
−
∂
H
∂
θ
=
−
λ
1
\begin{aligned} \dot\lambda_1&=-\frac{\partial H}{\partial \theta}=\lambda_2mgl\cos\theta/I\\ \dot\lambda_2&=-\frac{\partial H}{\partial \theta}=-\lambda_1 \end{aligned}
λ ˙ 1 λ ˙ 2 = − ∂ θ ∂ H = λ 2 m g l cos θ / I = − ∂ θ ∂ H = − λ 1
最优控制
∂
H
∂
u
=
R
u
+
λ
2
/
I
=
0
⟹
u
=
−
λ
2
/
R
I
\frac{\partial{H}}{\partial u}=Ru+\lambda_2/I=0\implies u=-\lambda_2/{RI}
∂ u ∂ H = R u + λ 2 / I = 0 ⟹ u = − λ 2 / R I
横截条件
H
(
t
f
)
+
∂
φ
(
x
f
)
∂
t
=
1
2
R
u
2
+
λ
2
u
/
I
=
0
⟹
λ
2
(
t
f
)
=
0
H(t_f)+\frac{\partial \varphi(x_f)}{\partial t}=\frac1 2\text R u^2+\lambda_2u/I=0\implies \lambda_2(t_f)=0
H ( t f ) + ∂ t ∂ φ ( x f ) = 2 1 R u 2 + λ 2 u / I = 0 ⟹ λ 2 ( t f ) = 0
代入数据,调用MATLAB中的
sol
=
bvp4c(odefun,bcfun,solinit,options)
\texttt{sol = bvp4c(odefun,bcfun,solinit,options)}
sol = bvp4c(odefun,bcfun,solinit,options)
轨道动力学方程
r
¨
=
−
μ
r
3
r
+
a
\mathbf{\ddot r}=\mathbf -\frac\mu{r^3}\mathbf r+\mathbf a
r ¨ = − r 3 μ r + a
r
(
t
0
)
=
r
0
,
v
(
t
0
)
=
v
0
r(t_0)=r_0,v(t_0)=v_0
r ( t 0 ) = r 0 , v ( t 0 ) = v 0
t
f
t_f
t f
ψ
(
r
(
t
f
)
,
v
(
t
f
)
)
=
r
T
v
=
0
\psi(\mathbf r(t_f),\mathbf v(t_f))=\mathbf r^{\mathrm T}\mathbf v=0
ψ ( r ( t f ) , v ( t f ) ) = r T v = 0
min
a
(
t
)
J
=
1
2
∫
t
0
t
f
a
T
a
d
t
\min_{a(t)}J=\frac1 2\int_{t_0}^{t_f}\mathbf a^{\mathrm T}\mathbf a\text d t
min a ( t ) J = 2 1 ∫ t 0 t f a T a d t
x
=
[
r
v
]
f
(
x
)
=
[
r
−
μ
r
3
r
+
a
]
\mathbf x=\begin{bmatrix}\mathbf r\\ \mathbf v\end{bmatrix}\\ \mathbf f(\mathbf x)=\begin{bmatrix}\mathbf r\\ -\frac\mu{r^3}\mathbf r+\mathbf a\end{bmatrix}
x = [ r v ] f ( x ) = [ r − r 3 μ r + a ]
则Hamilton函数为
H
=
1
2
a
T
a
+
λ
r
T
v
+
λ
v
T
(
g
(
r
)
+
a
)
H=\frac 1 2\mathbf a^{\mathrm T}\mathbf a+\mathbf\lambda_r^{\mathrm T}\mathbf v+\mathbf\lambda_v^{\mathrm T}(\mathbf g(\mathbf r)+\mathbf a)
H = 2 1 a T a + λ r T v + λ v T ( g ( r ) + a )
协态方程
λ
˙
r
T
=
−
∂
H
∂
r
=
−
λ
v
T
∂
g
(
r
)
∂
r
λ
˙
v
T
=
−
∂
H
∂
v
=
−
λ
r
T
\begin{aligned} \dot{\lambda}_{r}^{\mathrm T}&=-\frac{\partial H}{\partial \mathbf{r}}=-\lambda_{\mathrm{v}}^{\mathrm T} \frac{\partial \mathbf{g}(\mathbf{r})}{\partial \mathbf{r}}\\ \dot{\lambda}_{\mathrm{v}}^{\mathrm T}&=-\frac{\partial H}{\partial \mathbf{v}}=-\lambda_{r}^{\mathrm T} \end{aligned}
λ ˙ r T λ ˙ v T = − ∂ r ∂ H = − λ v T ∂ r ∂ g ( r ) = − ∂ v ∂ H = − λ r T
对终端约束引入Lagrange乘数
μ
∈
R
1
\mu\in\Reals^1
μ ∈ R 1
λ
r
(
t
f
)
=
μ
T
∂
ψ
∂
r
(
t
f
)
=
μ
v
f
λ
v
(
t
f
)
=
μ
T
∂
ψ
∂
v
(
t
f
)
=
μ
r
f
\lambda_{r}\left(t_{f}\right)=\mu^{\mathrm T}\frac{\partial\psi}{\partial \mathbf{r}\left(t_{f}\right)}=\mu\mathbf v_f \\ \lambda_{\mathrm{v}}\left(t_{f}\right)=\mu^{\mathrm T}\frac{\partial\psi}{\partial \mathbf{v}\left(t_{f}\right)}=\mu\mathbf r_f
λ r ( t f ) = μ T ∂ r ( t f ) ∂ ψ = μ v f λ v ( t f ) = μ T ∂ v ( t f ) ∂ ψ = μ r f
最优控制
∂
H
∂
a
=
a
+
λ
v
=
0
(9)
\frac{\partial{H}}{\partial \mathbf a}=\mathbf a+\lambda_v=0\tag 9
∂ a ∂ H = a + λ v = 0 ( 9 )
a
=
−
λ
v
\mathbf a=-\lambda_{\mathbf v}
a = − λ v
(
9
)
(9)
( 9 )
r
˙
=
r
v
˙
=
−
μ
r
3
r
−
λ
v
λ
˙
r
T
=
−
λ
v
T
∂
g
(
r
)
∂
r
λ
˙
v
T
=
−
λ
r
T
\begin{aligned} \dot\mathbf r&=\mathbf r\\ \dot\mathbf v&= -\frac\mu{r^3}\mathbf r-\lambda_v\\ \dot{\lambda}_{r}^{\mathrm T}&=-\lambda_{\mathrm{v}}^{\mathrm T} \frac{\partial \mathbf{g}(\mathbf{r})}{\partial \mathbf{r}}\\ \dot{\lambda}_{\mathrm{v}}^{\mathrm T}&=-\lambda_{r}^{\mathrm T} \end{aligned}
r ˙ v ˙ λ ˙ r T λ ˙ v T = r = − r 3 μ r − λ v = − λ v T ∂ r ∂ g ( r ) = − λ r T
1个未知常数
μ
\mu
μ
[1] 邢继祥. 最优控制应用基础[M]. 科学出版社, 2003.最优控制理论 二+、哈密尔顿函数法的补充
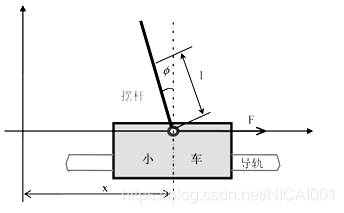 首先写出一阶非线性微分方程组
首先写出一阶非线性微分方程组