插值算法
一、插值算法概述
插值算法的作用:在数学建模中,常常需要根据已知的函数点进行数据、模型的处理和分析,而有时候现有的数据是极少的,不足以支撑分析的进行,这个时候就需要使用一些数学的方法,‘模拟产生’一些新的但是又比较靠谱的值来满足需求。




二、常用插值法
1、拉格朗日插值法

当有三个点的时候

龙格现象
在数值分析领域中,龙格现象是在一组等间插值点上使用具有高次多项式的多项式插值时出现的区间边缘处的振荡问题。 它是由卡尔・龙格(Runge)在探索使用多项式插值逼近某些函数时的错误行为时发现的。 这一发现非常重要,因为它表明使用高次多项式插值并不总能提高准确性。 该现象与傅里叶级数近似中的吉布斯现象相似。
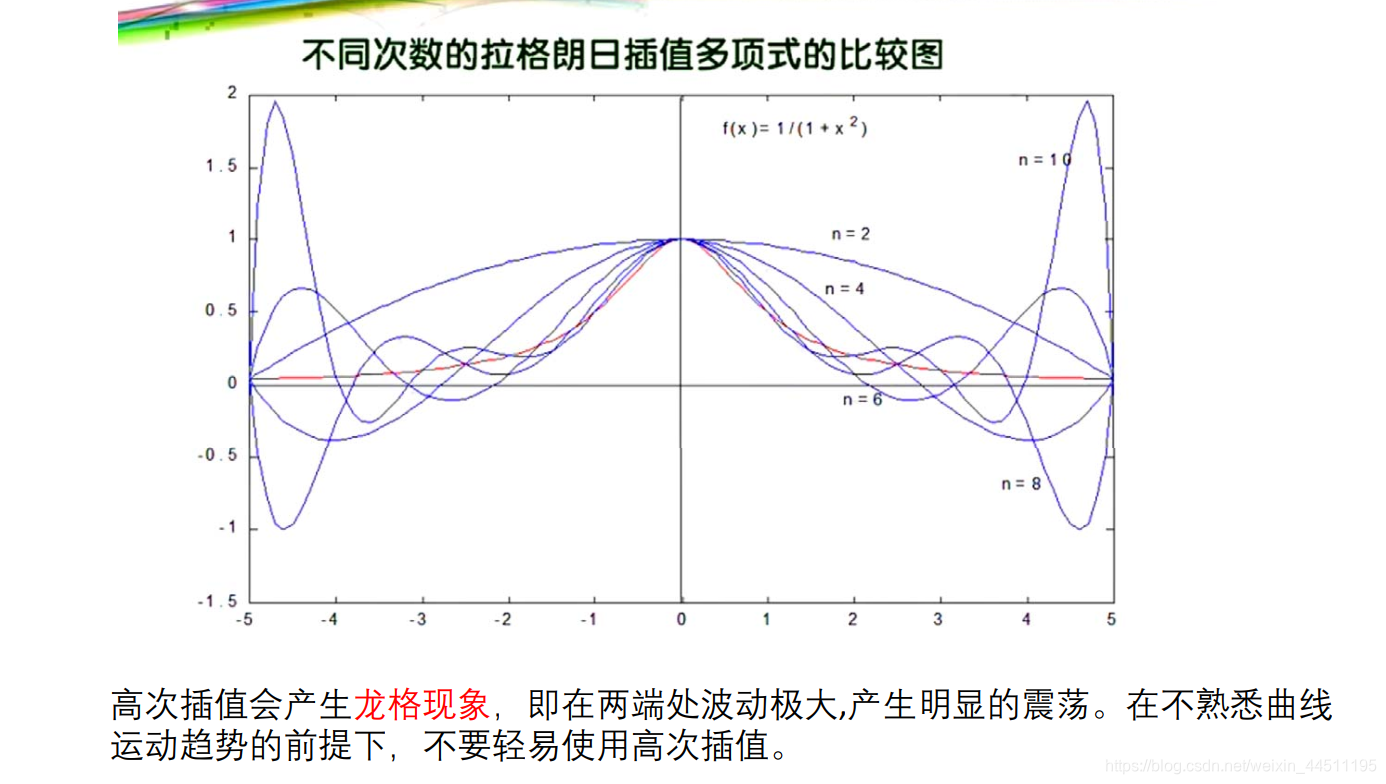
解决龙格现象
分段线性插值
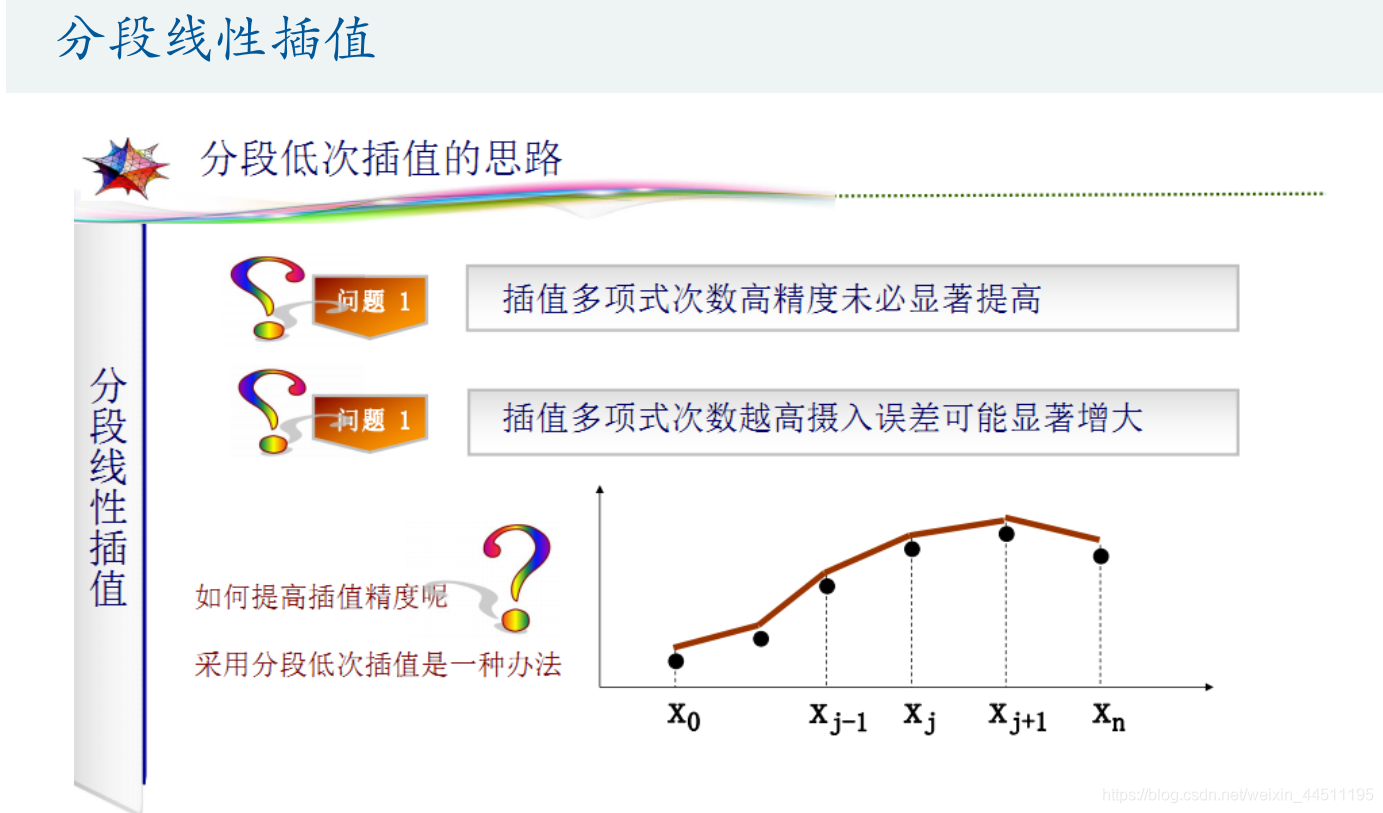
分段二次插值

2、牛顿插值法

两种插值法对比

但是这两种插值法都无法反映出被插函数的性态。
3、埃尔米特插值法
不少实际的插值问题不但要求在节点上的函数值相等,而且还要求对应的导数值也相等,甚至要求高阶导数也相等,满足这种要求的插值多项式就是埃尔米特插值多项式。


4、分三段埃尔米特插值法(重点)
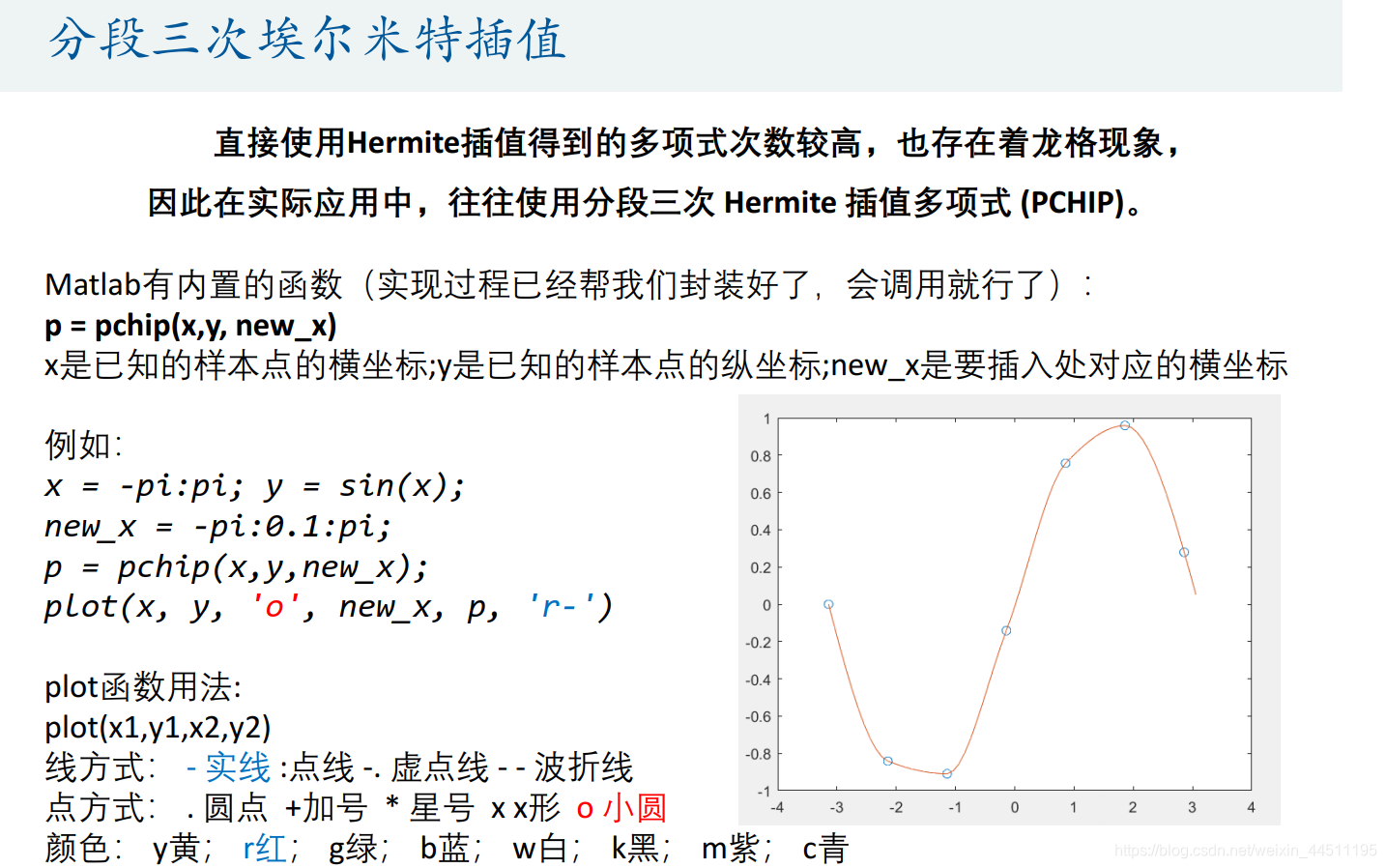
代码如下:
x = -pi:pi; y = sin(x);
new_x = -pi:0.1:pi;
p = pchip(x,y,new_x);
figure(1);
plot(x, y, 'o', new_x, p, 'r-')

5、三次样条插值


代码如下:
% 三次样条插值和分段三次埃尔米特插值的对比
x = -pi:pi;
y = sin(x);
new_x = -pi:0.1:pi;
p1 = pchip(x,y,new_x); %分段三次埃尔米特插值
p2 = spline(x,y,new_x); %三次样条插值
figure(2);
plot(x,y,'o',new_x,p1,'r-',new_x,p2,'b-')
legend('样本点','三次埃尔米特插值','三次样条插值','Location','SouthEast')
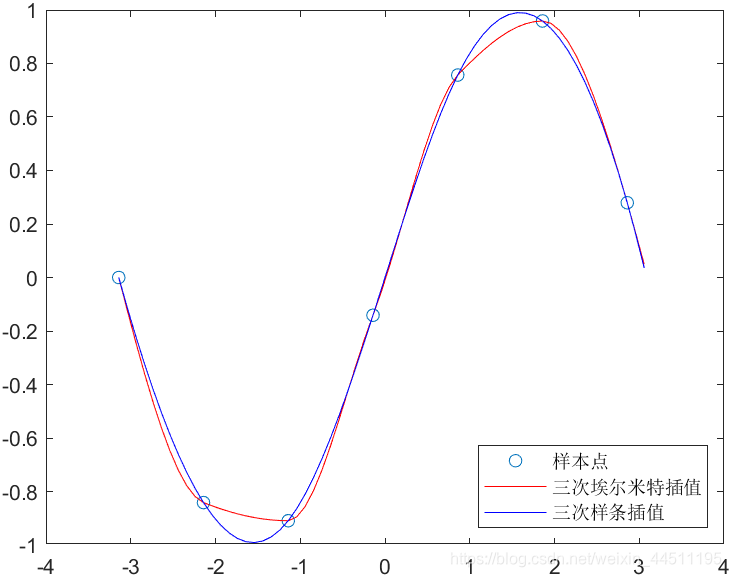
符合状态较好,但是条件难以满足。
6、n维数据的插值(了解)
