DDA画线算法

定义

通过单位间隔来确定线段的点,默认间隔为1,如图: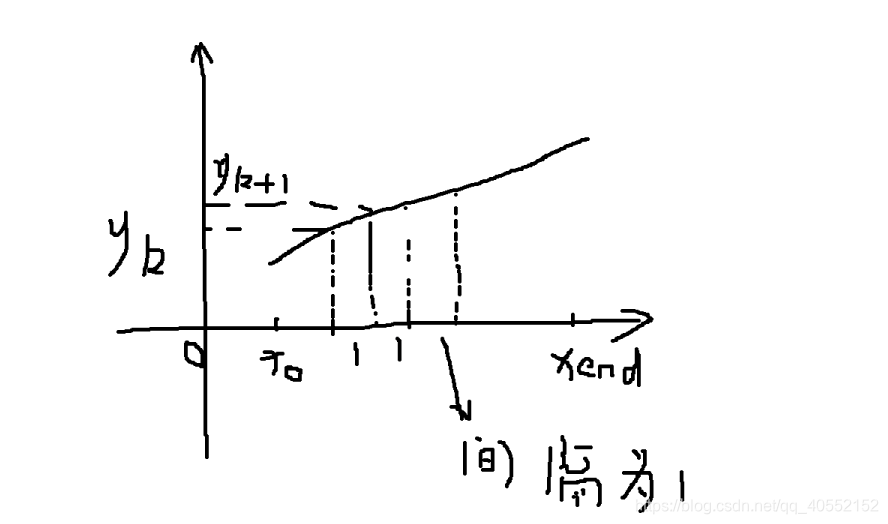 在这里插入图片描述
此时,已知的点为 $(x_0,y_0), (x_{end},y_{end})$ ,假设 $y_k与y_{k+1}$ 是两点连线上的点的纵坐标

公式推导

设直线方程为: $y = mx + b,m=\frac{y_{end}-y0}{x_{end}-x_0}$
此时进行分类讨论:
当m大小小于等于1时,则 $x$ 每次递增1,即 $\Delta x=1$ , $y$ 每次递增为 $m$ ,公式如下:
$y_{k+1} = y_k + m\Delta x(\Delta x=1)$
反之,当m大小大于1时,则 $y$ 每次递增1,即 $\Delta y=1$ , $x$ 每次递增为 $\frac{1}{m}$ ,
$x_{k+1}=x_k+\frac{1}{m}\Delta y(\Delta y=1)$

代码实现

#include <windows.h>
#include <GL/glu.h>
#include <GL/gl.h>
#include <GL/glut.h>
#include <math.h>
#include <stdlib.h>

// DDA算法
void lineDDA(int x0, int y0, int xend, int yend) {
	int dx = xend - x0, dy = yend - y0; // 两点间的横,纵坐标间隔
	float xIncrement, yIncrement, x = x0, y = y0; // 初始化x,y
	int steps;

	if (fabs(dx) >= dy) { // 当斜率小于等于1时
		steps = fabs(dx);
	}
	else // 当斜率大小大于1时
	{
		steps = fabs(dy);
	}
	// 设置 Δx, Δy 的大小
	xIncrement = float(dx) / float(steps);
	yIncrement = float(dy) / float(steps);
	
	//开始画点
	glClear(GL_COLOR_BUFFER_BIT);
	glBegin(GL_POINTS);
	glVertex2i(x0, y0);
	for (int i = 0; i < steps; i++)
	{
		x += xIncrement;
		y += yIncrement;
		glVertex2f(x, y);
	}
	glVertex2i(xend, yend);
	glEnd();
	glFlush();
}

// 主方法
void display() {
	glClear(GL_COLOR_BUFFER_BIT);
	glViewport(100, 100, 500, 500);
	lineDDA(30, 35, 140, 200);
}

// 初始化该方法
void Init() {
	glClearColor(1.0, 1.0, 1.0, 0.0);
	glPointSize(5.0);
	glColor3f(0.0, 0.0, 0.0);
	gluOrtho2D(0.0, 600.0, 0.0, 600.0);
	glMatrixMode(GL_MODELVIEW);
}

int main(int argc, char* argv[]) {
	glutInit(&argc, argv);
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
	glutInitWindowSize(600, 600);
	glutInitWindowPosition(0, 0);
	glutCreateWindow("lineDDA");
	glutDisplayFunc(display);
	Init();
	glutMainLoop();

	return 0;
}

效果

在这里插入图片描述

缺点

在浮点增量的连续叠加中,会造成取整的误差问题,是像素位置偏离实际线段,而且该过程的取整与浮点运算仍十分耗时

Bresenham画线算法

定义

该算法属于增量整数计算,不会涉及浮点数的叠加问题.Bresenham算法采用的是逐步递推的方法来确定下一个像素点的位置.注:像素点只能取整数坐标!!!!!

公式推导

首先我们来看一个示例:

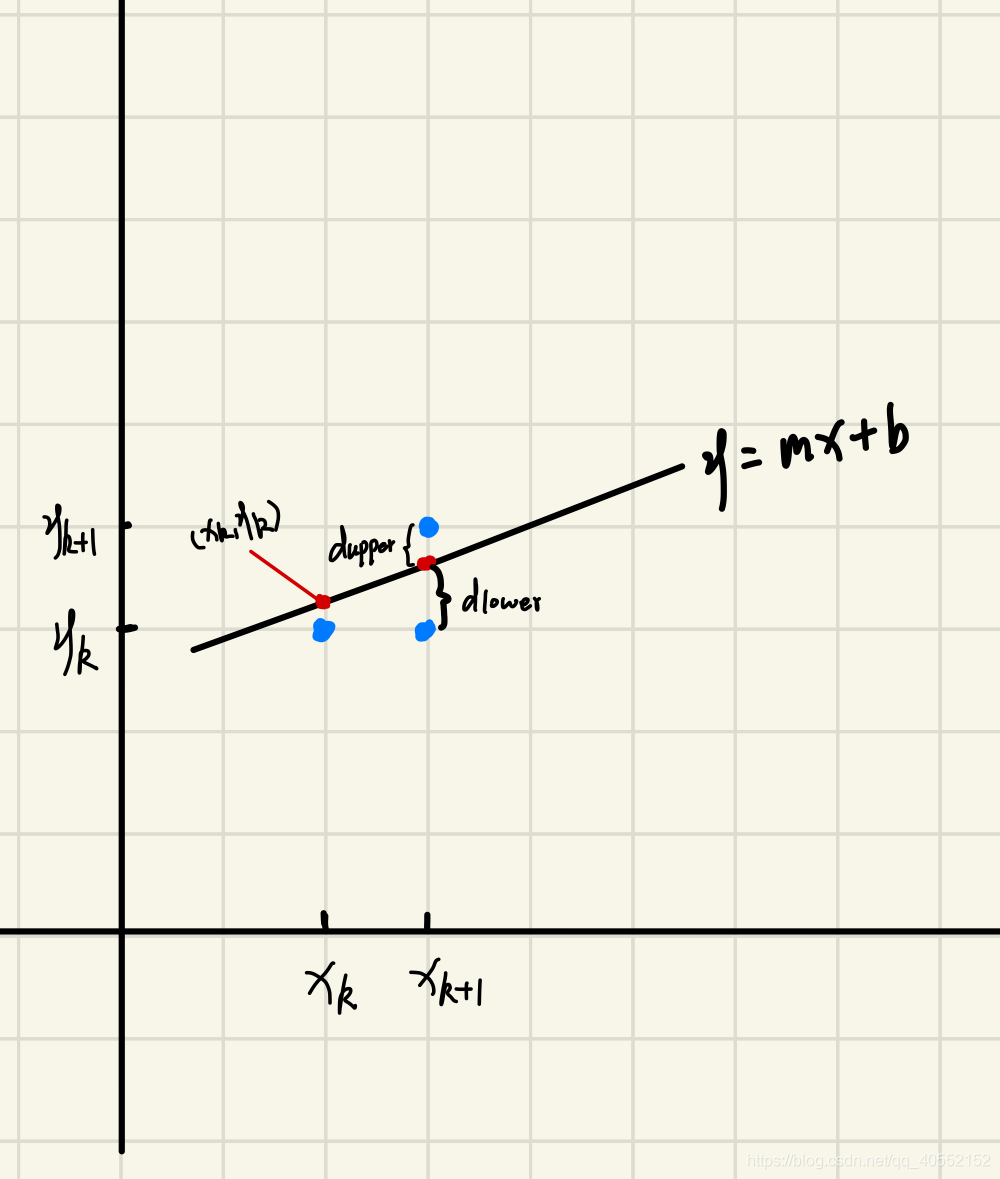
在该图中只能取整数点的像素坐标, 由于第k个像素点与 $(x_k,y_k)$ 点最为接近,所以先假设第k个像素点坐标为 $(x_k,y_k)$ ,那么第k+1个像素点的位置可能为 $(x_{k+1},y_k)或(x_{k+1},y_{k+1})$ ,这是我们需要计算该点与上述两点哪个最为接近.
我们知道该直线方程为: $y=mx+b$ , $\Delta y 与\Delta x$ 为两端点垂直与水平偏移量, $m=\frac{\Delta y}{\Delta x}$ ,那么在 $x_{k+1}$ 处的y的坐标为: $y=m(x_{k+1})+b=m(x_k+1)+b$
- 该点到 $y_k$ 的距离为: $d_{lower}=y-y_k=m(x_k+1)+b-y_k$
- 该点到 $y_k+1$ 的距离为: $d_{upper}=y_{k+1}-y=(y_k+1)-y=(y_k+1)-m(x_k+1)-b$
然后我们就可以比较他们距离的大小 $d_{lower}-d_{upper}=2m(x_k+1)-2y_k+2b-1$
- 若结果小于0,说明跟下面的像素点最接近,就选择 $(x_{k+1},y_k)$
- 若大于等于0,则选择 $(x_{k+1},y_{k+1})$
通过上述公式的对比可以发现,像素点的选择只取决于 $(d_{lower}-d_{upper})$ 的符号且通过 $(x_k,y_k)$ 便可以确定下一个点的位置,为了方便我们的计算,引入了新的变量 $p_k$ ,作为我们的决策参数
$p_k=\Delta x(d_{lower}-d_{upper})=2\Delta y*x_k-2\Delta x*y_k +2\Delta y+\Delta x(2b-1)$ ,其中 $2\Delta y+\Delta x(2b-1)$ 为常数,我们用 $c$ 来代替,于是 $p_k=\Delta x(d_{lower}-d_{upper})=2\Delta y*x_k-2\Delta x*y_k +c$ 注:由于Δ x>0,所以对pk的正负符号无影响
同理 $p_{k+1} =2\Delta y*(x_{k+1})-2\Delta x*y_{k+1}+c(x_{k+1}=x_k+1)$
$p_{k+1}-p_k =2\Delta y(x_{k+1}-x_k)-2\Delta x(y_{k+1}-y_k) \implies p_{k+1}=p_k +2\Delta y(x_{k+1}-x_k)-2\Delta x(y_{k+1}-y_k) =p_k+2\Delta y-2\Delta x(y_{k+1}-y_k)$
- 当 $p_k>0,y_{k+1}=y_k$
- 当 $p_k<= 0,y_{k+1} = y_k+1$
求初始值 $p_0=2\Delta y*x_0-2\Delta x*y_0+2\Delta y+\Delta x(2b-1)=2mx_0\Delta x-2\Delta x(mx_0+b)+2\Delta y+\Delta x(2b-1)=2\Delta y-\Delta x$
$|m|<1时的Bresenham算法流程$ :

代码实现

#include <windows.h>
#include <GL/glu.h>
#include <GL/gl.h>
#include <GL/glut.h>
#include <math.h>
#include <stdlib.h>

// Bresenham 算法
void lineBresenham(int x0, int y0, int xend, int yend) {
	int dx = fabs(xend - x0), dy = fabs(yend - y0);
	int p = 2 * dy - dx;
	int twoDy = 2 * dy, twoDyMinusDx = 2 * (dy - dx);
	int x, y;
	// 确定开始位置
	if (x0 > xend) // x0在右侧
	{
		x = xend;
		y = yend;
		xend = x0;
	}
	else // x0在左侧
	{
		x = x0;
		y = y0;
	}
	glClear(GL_COLOR_BUFFER_BIT);
	glBegin(GL_POINTS);
	glVertex2f(x, y);
	while (x<xend)
	{
		x++;
		if (p<0)
		{
			p += twoDy;
		}
		else {
			y++;
			p += twoDyMinusDx;
		}
		glVertex2f(x, y);
	}
	glEnd();
	glFlush();
}

// 主方法
void display() {
	glClear(GL_COLOR_BUFFER_BIT);
	glViewport(100, 100, 500, 500);
	lineBresenham(40, 45, 140, 135);
}

// 初始化该方法
void Init() {
	glClearColor(1.0, 1.0, 1.0, 0.0);
	glPointSize(5.0);
	glColor3f(0.0, 0.0, 0.0);
	gluOrtho2D(0.0, 600.0, 0.0, 600.0);
	glMatrixMode(GL_MODELVIEW);
}

int main(int argc, char* argv[]) {
	glutInit(&argc, argv);
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
	glutInitWindowSize(600, 600);
	glutInitWindowPosition(0, 0);
	glutCreateWindow("lineDDA");
	glutDisplayFunc(display);
	Init();
	glutMainLoop();

	return 0;
}

效果

在这里插入图片描述