@本文来源于公众号:csdn2299,喜欢可以关注公众号 程序员学府
退火算法就是钢铁在淬炼过程中失温而成稳定态时的过程,热力学上温度(内能)越高原子态越不稳定。这篇文章主要介绍了Python退火算法在高次方程的应用,需要的朋友可以参考下
一,简介
退火算法不言而喻,就是钢铁在淬炼过程中失温而成稳定态时的过程,热力学上温度(内能)越高原子态越不稳定,而温度有一个向低温区辐射降温的物理过程,当物质内能不再降低时候该物质原子态逐渐成为稳定有序态,这对我们从随机复杂问题中找出最优解有一定借鉴意义,将这个过程化为算法,具体参见其他资料。
二,计算方程
我们所要计算的方程是f(x) = (x - 2) * (x + 3) * (x + 8) * (x - 9),是一个一元四次方程,我们称为高次方程,当然这个函数的开口是向上的,那么在一个无限长的区间内我们可能找不出最大值点,因此我们尝试在较短区间内解最小值点,我们成为最优解。
解法一:
毫无疑问,数学方法多次求导基本可以解出,但是这个过程较复杂,还容易算错,我就不赘述了,读者有时间自己可以尝试解一下。
解法二:
这个解法就是暴力解决了,我们这里只求解区间[-10,10]上的最优解,直接随机200个点,再除以10(这样可以得到非整数横坐标),再依此计算其纵坐标f(x),min{f(x)}一下,用list的index方法找出最小值对应位置就行了,然后画出图形大致瞄一瞄。
直接贴代码:
import random
import matplotlib.pyplot as plt
list_x = []
# for i in range(1):
# #print(random.randint(0,100))
# for i in range(0,100):
# print("sss",i)
#
# list_x.append(random.randint(0,100))
for i in range(-100,100):
list_x.append(i/10)
print("横坐标为:",list_x)
print(len(list_x))
list_y = []
for x in list_x:
# print(x)
#y = x*x*x - 60*x*x -4*x +6
y = (x - 2) * (x + 3) * (x + 8) * (x - 9)
list_y.append(y)
print("纵坐标为:",list_y)
#经验证,这里算出来的结果6.5和最优解1549都是对的
print("最小值为:",min(list_y))
num = min(list_y)
print("最优解:",list_y.index(num)/10)
print("第",list_y.index(num)/10-10,"个位置取得最小值")
plt.plot(list_x, list_y, label='NM')
#plt.plot(x2, y2, label='Second Line')
plt.xlabel('X') #横坐标标题
plt.ylabel('Y') #纵坐标标题
#plt.title('Interesting Graph\nCheck it out',loc="right") #图像标题
#plt.title('Interesting Graph\nCheck it out')
plt.legend() #显示Fisrt Line和Second Line(label)的设置
plt.savefig('C:/Users/zhengyong/Desktop/1.png')
plt.show()
得到如下结果:
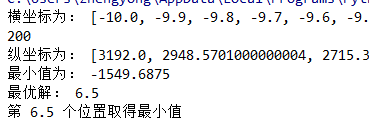
那么我们得出最优解的坐标是(6.5,-1549.6875),结果先放这里,接下来用退火算法看能不能解出。
解法三:
我们看一张图(解法二中的方法得出的图),然后讲讲退火算法的最核心的思想。

首先,先随机一个[-10.10]之间的随机解,作为初始解空间,比方说随机了一个位于[-2.5.2.5]中最高的那个点就是点1(横坐标为x1),他有对于的纵坐标的值y1,这时候我们把这个点的横坐标随机加或者减去一个值(注意这个值的大小很重要,我们先叫他随机移动值),加或者减后得到新的横坐标的值x2,再算出这个横坐标的对应纵坐标(y2),对比之前的纵坐标的大小,这里设置
delta = y2-y1,发现无论怎样都是小于原先的纵坐标(前提是随机移动值足够小),这时候我们把新得到的x2赋值给x1,这时候现在的x2的值传给x1,x1是原先随机的值,这个过程可以重复iter_num 次,大小就根据自己的区间来。
上述的整个过程是在一个温度下进行的,这个过程结束后我们用温度更新公式再次的更新温度,再去重复上述步骤。
温度更新我是用的常用的公式是T(t)=aT0(t-1),其中0.85≦a≦0.99。也可用相应的热能衰减公式来计算,T(t)=T0/(1+lnt),t=1,2,3,…,这都是简单的状态更新方法。
也就是说,不管你随机的是几我都能朝着优化的方向前进(前提是非最优点)。
其次,点2 是同理的,区别在于他是局部最优解,那么跳出这个局部最优解的机制是什么呢?
若初始点是(x3,y3),然后用上述方法得出(x4,y4),在点二处得到的delta肯定是大于0的,那么怎么办呢?当大于0的时候我们每次都有一定的概率来接受这个看起来不是最优的点,叫Metropolis准则,具体是这样的:
这里的E就是y,T就是当前温度,delta小于0就是百分百接受新值,否者就是按照这个概率接受,当迭代多次的时候,每次向右移动的步长累加到点1 时候他就有可能找到最终的最优解了,步长是累加的但是概率是累成的,意味着这个概率很小,但是一旦迭代次数多久一定会跑出来到最优解处。
最优,点3不解释了哈,和上面一样。
那么我们上代码:
#自己改写的退火算法计算方程(x - 2) * (x + 3) * (x + 8) * (x - 9)的计算方法
#class没啥用
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import pyplot as plt
#设置基本参数
#T初始温度,T_stop,iter_num每个温度的迭代次数,Q温度衰减次数
class Tuihuo_alg():
def __init__(self,T_start,iter_num,T_stop,Q,xx,init_x):
self.T_start = T_start
self.iter =iter_num
self.T_stop = T_stop
self.Q = Q
self.xx = xx
self.init_x = init_x
# def cal_x2y(self):
# return (x - 2) * (x + 3) * (x + 8) * (x - 9)
if __name__ == '__main__':
def cal_x2y(x):
#print((x - 2) * (x + 3) * (x + 8) * (x - 9))
return (x - 2) * (x + 3) * (x + 8) * (x - 9)
T_start = 1000
iter_num = 1000
T_stop = 1
Q = 0.95
K = 1
l_boundary = -10
r_boundary = 10
#初始值
xx = np.linspace(l_boundary, r_boundary, 300)
yy = cal_x2y(xx)
init_x =10 * ( 2 * np.random.rand() - 1)
print("init_x:",init_x)
t = Tuihuo_alg(T_start,iter_num,T_stop,Q,xx,init_x)
val_list = [init_x]
while T_start>T_stop:
for i in range(iter_num):
init_y = cal_x2y(init_x)
#这个区间(2 * np.random.rand() - 1)本身是(-1,1),所以加上就是一个随机加或者减过程
new_x = init_x + (2 * np.random.rand() - 1)
if l_boundary <= new_x <= r_boundary:
new_y = cal_x2y(new_x)
#print("new_x:",new_x)
#print('new_y:',new_y)
delta = new_y - init_y #新减旧
if delta < 0:
init_x = new_x
else:
p = np.exp(-delta / (K * T_start))
if np.random.rand() < p:
init_x = new_x
#print("new_x:",new_x)
#print("当前温度:",T_start)
T_start = T_start * Q
print("最优解x是:", init_x) #这里最初写的是new_x,所以结果一直不对
print("最优解是:", init_y)
#比如我加上new_x,真假之间的误差实际就是最后一次的赋值“init_x = new_x”
print("假最优解x是:", new_x) #这里最初写的是new_x,所以结果一直不对
print("假最优解是:", new_y)
xx = np.linspace(l_boundary,r_boundary,300)
yy = cal_x2y(xx)
plt.plot(xx, yy, label='Tuihuo')
#plt.plot(x2, y2, label='Second Line')
plt.xlabel('X for tuihuo') #横坐标标题
plt.ylabel('Y for tuihuo') #纵坐标标题
#plt.title('Interesting Graph\nCheck it out',loc="right") #图像标题
#plt.title('Interesting Graph\nCheck it out')
plt.legend() #显示Fisrt Line和Second Line(label)的设置
plt.savefig('C:/Users/zhengyong/Desktop/1.png')
plt.show()
这里用了class,发现并不需要,但是不想改了,就这样吧。
最优结果为:

得出的示意图为:
三,总结
退火算法的具体思想我没怎么讲,但是核心的点我都写出来了,经过验证发现退火算法得出了(6.551677228904226,-1548.933671426107)的最优解,看看解法二的(6.5,-1549.6875),我们发现,呵呵,差不多,误差来讲的话,能接受,当然读者也可以多跑几个数据出来验证。
我的实验环境是Python3.6,Numpy1.14.3,matplotlib2.2.2,64位win10,1709教育版,OS内核16299.547,就这样吧,尽量讲详细点。
非常感谢你的阅读
大学的时候选择了自学python,工作了发现吃了计算机基础不好的亏,学历不行这是没办法的事,只能后天弥补,于是在编码之外开启了自己的逆袭之路,不断的学习python核心知识,深入的研习计算机基础知识,整理好了,我放在我们的微信公众号《程序员学府》,如果你也不甘平庸,那就与我一起在编码之外,不断成长吧!
其实这里不仅有技术,更有那些技术之外的东西,比如,如何做一个精致的程序员,而不是“屌丝”,程序员本身就是高贵的一种存在啊,难道不是吗?[点击加入]
想做你自己想成为高尚人,加油!
