终于开始补省冬的锅了/kk
学习笔记参考[xMinh dalao 的博客](https://xminh.github.io/2018/02/27/%E5%90%8E%E7%BC%80%E6%95%B0%E7%BB%84-%E6%9C%80%E8%AF%A6%E7%BB%86(maybe)%E8%AE%B2%E8%A7%A3.html)
#### 一、后缀数组的相关定义
1.子串:在字符串$s$中,取任意$i \le j$,那么在$s$中截取**从$i$到$j$** 的这一段就叫做$s$的一个**子串**
。
2.前缀:$s[1...i]$,$1 \le i \le n$。
3.后缀:$s[i...n]$,$1 \le i \le n$。
后缀数组:
对于一个字符串$s$的后缀按照**字典序排序**的结果。
记$suff(i)$为$s[i...n]$。
$sa_i$表示**排名为i的后缀的起始位置**,$rank_i$表示**从i开始的后缀的排名**,也就是说$rank_{sa_i}$=$i$。
#### 二、求$sa_i$的方法——倍增
复杂度$O(n log n)$
暴力复杂度$O(n^2 log n)$
- 读入字符串后进行排序(按照每个后缀的**第一个**字符排序)。
- 对于每一个字符,我们按照**字典序**给一个**排名**,这里也叫**关键字**。
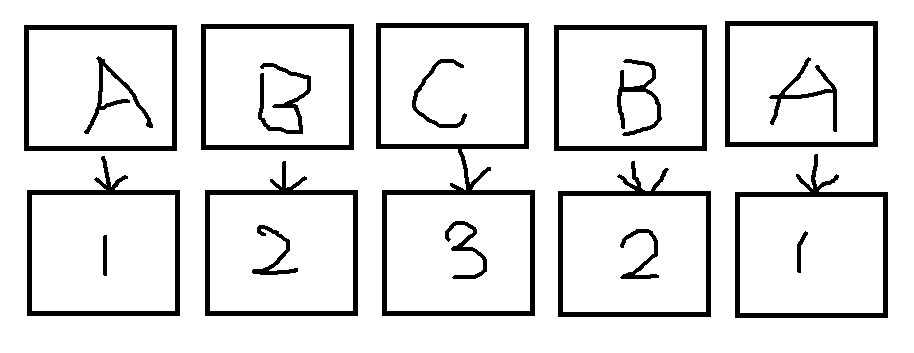
- 此时再把**相邻**两个关键字合并,以第一个字母的排名为**第一关键字**,第二个字母的排名为**第二关键字**,没有第二关键字的设为$0$。
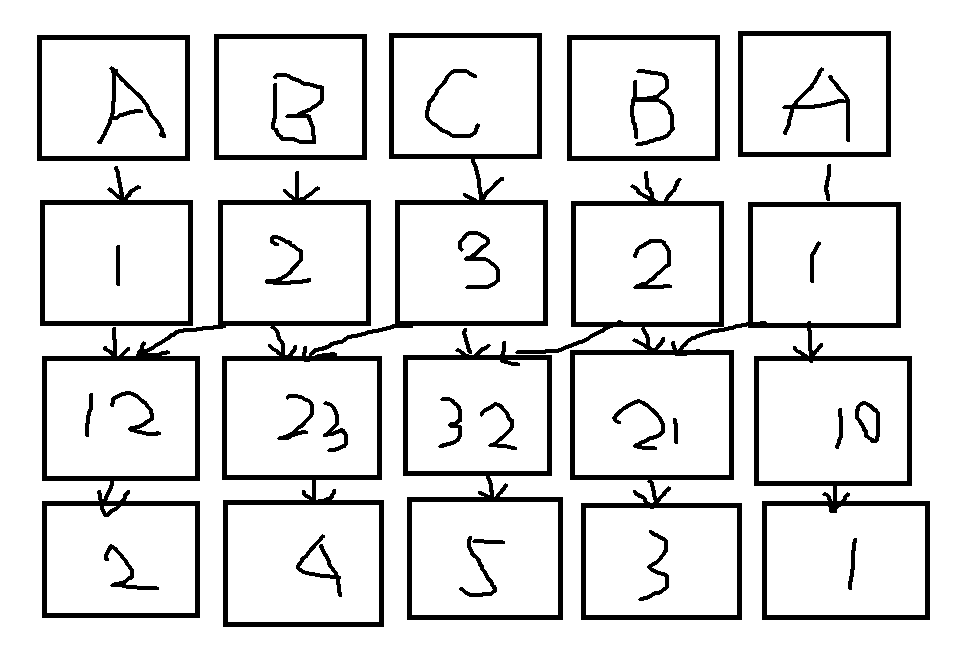
- 注意到现在第$i$位上的关键字为 **$suff(i)$的前两个字符的排名** ,而第$i+2$位上的关键字为 **$suff(i+2)$的前两个字符的排名** ,所以合并起来就是 **$suff(i)$的前四个字符的排名**
- 这就运用到倍增的思想
- 显然,当所有排名都不同的时候就可以退出啦!
- 时间复杂度稳定在 $O(log n)$。
#### 三、基数排序(桶排序)
用快排的话是$O(nlog^2n)$的,注意到每次排序都是排两个数的,所以设两个桶$x$ , $y$ ,一个存**第一关键字**,一个存**第二关键字**,每次排序的复杂度为$O(n)$。
优化后的复杂度为$O(nlogn)$
#### Code:
#include<iostream> #include<cstring> #include<cstdio> using namespace std; const int maxn=1e6+5; char s[maxn]; int sa[maxn],x[maxn],y[maxn],rank[maxn],c[maxn]; int n,m; //sa[i]表示排名为i的后缀的起始位置,rank[i]表示从i开始的后缀的排名,也就是说sa[i]和rank[i]反过来的 //x[i],y[i]分别为第i个元素的第1关键字和第2关键字 //c[i]为桶 inline void SA(){ for(int i=1;i<=n;i++) ++c[x[i]=s[i]]; for(int i=2;i<=m;i++) c[i]+=c[i-1];//得出每个关键字最多在第几名 for(int i=n;i>=1;i--) sa[c[x[i]]--]=i; for(int k=1;k<=n;k<<=1){//倍增 int num=0; for(int i=n-k+1;i<=n;i++) y[++num]=i;//显然,第n-k+1~n位无第二关键字 for(int i=1;i<=n;i++) if(sa[i]>k) y[++num]=sa[i]-k; //排名为i的数 在数组中是否在第k位以后 //如果满足(sa[i]>k) 那么它可以作为别人的第二关键字,就把它的第一关键字的位置添加进y就行了 //所以i枚举的是第二关键字的排名,第二关键字靠前的先入队 for(int i=1;i<=m;i++) c[i]=0;//初始化 for(int i=1;i<=n;i++) ++c[x[i]]; for(int i=2;i<=m;i++) c[i]+=c[i-1]; for(int i=n;i>=1;i--) sa[c[x[y[i]]]--]=y[i],y[i]=0; //因为y的顺序是按照第二关键字的顺序来排的 //第二关键字越靠后的,在同一个第一关键字桶中排名越靠后 //基数排序 swap(x,y); num=1;x[sa[1]]=1; for(int i=2;i<=n;i++) x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?num:++num; if(num==n) break; m=num; } for(int i=1;i<=n;i++) printf("%d ",sa[i]); return; } int main(){ scanf("%s",s+1); n=strlen(s+1);m=122;//'z'的ASCLL码是122 SA(); return 0; }
#### 四、后缀数组的辅助工具——最长公共前缀$(LCP)$
1. 定义:$LCP(i,j)$为$suff(i)$和$suff(j)$的最长公共前缀。
2. 显然:
$LCP(i,j)$=$LCP(j,i)$。
$LCP(i,i)=n-sa_i+1$。
3. 性质:
$LCP(i,k)=min(LCP(i,j),LCP(j,k))$ $(1 \le i \le j \le k \le n)$
$LCP(i,k)=min(LCP(j,j-1))$ $(1 \le i \le j \le k \le n)$
~~懒得证明了hhh~~
**重点!那么如何求LCP呢**
定义$height_i$为$LCP(i,i-1)$。
特别的$height_1=0$
最关键的一条性质:$height[rank_i]>=height[rank_{i-1}]-1$
证明:
$height[rank[i-1]]=0$时显然
否则设$u=sa[rank[i-1]-1],v=sa[rank[i-1]]=i-1$
必有$s[u]=s[v]$
由于$s_u$的排名小于$s_v$,所以$s_{u+1}$的排名必然小于$s_v$
所以必然存在一个排名小于$s_u$的后缀,与$suff(sa_i)$的LCP长度$>=height[rank[i-1]]-1$
~~被自己绕晕了~~
所以我们拥有了一个$O(n)$求$height$数组的优秀做法~~~
按照$rank_1 rank_2 ... rank_n$的顺序求
设$k=height_{rank_i}$
求完$rank_{i-1}$求$rank_i$,如果$k>0$就$k--$。
检查$s[i+k]$是否等于$s[rank[i-1]+k]$,如果是就$k++$
最后 **$height_{rank_i}=k$**
#### Code
inline void LCP(){ int k=0; for(int i=1;i<=n;i++) rank[sa[i]]=i; for(int i=1;i<=n;i++){ if(rank[i]==1) continue; if(k) k--;//h[i]>=h[i-1]+1; int j=sa[rank[i]-1]; while(i+k<=n&&j+k<=n&&s[i+k]==s[j+k]) k++; h[rank[i]]=k; } for(int i=1;i<=n;i++) printf("%d ",h[i]); return ; }
所以$LCP(i,j)$为$height$数组中第$rank_i+1$到第$rank_j$个数的**最小值**,可以$O(nlogn)$预处理RMQ,$O(1)$回答
应用:求一个串$s$中**本质不同**的子串个数
一个串的子串可以表示为这个串的**一个后缀的前缀**
所以本质不同的串的个数相当于所有后缀的集合中,本质不同的前缀的个数
加入后缀$s[sa[i]...n]$后会产生$n-sa_i+1$个子串
显然子串中所有长度$\le height_i$的子串都已经在前面出现过了 ($height_i$可以表示为比$sa_i$小的后缀与$sa_i$的LCP**最大值**)
所以本质不同的串的个数为
$\sum\limits_{i=1}^{n}{(n-sa_i+1-height_i)}$$=\left(\dfrac {n*(n+1)} 2\right)-$$\sum\limits_{i=2}^{n}height_i$