2019-9 ccf csp认证考试第五题城市规划题目详解

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_43723614/article/details/103500010

2019年9月ccf城市规划题解

1. 题目描述

2. 设计方案

由题意抽象出数据结构:一颗无向树,N个节点,N-1条边,任意两个节点都是连通的,所以任意两个节点都存在连通距离L(ij)（可经过别的节点）。需要从其中规定的M个节点中选择出K个节点，使得K个节点间两两间的连通距离之和最短。

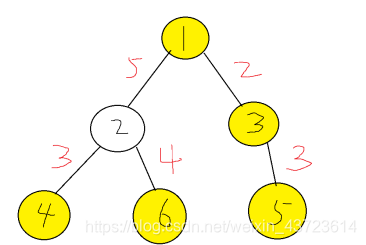
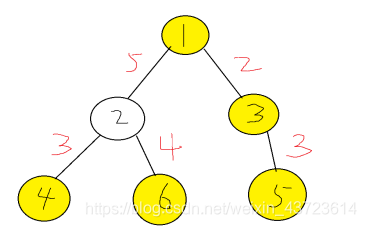
分析题意，如下图举例说明，求K个节点间两两间的连通距离之和最短等价于求所需重要节点对每条边的贡献之和，比如下图两个红圈之间的桥梁边对答案的贡献2*(k-2)*weight(权重);

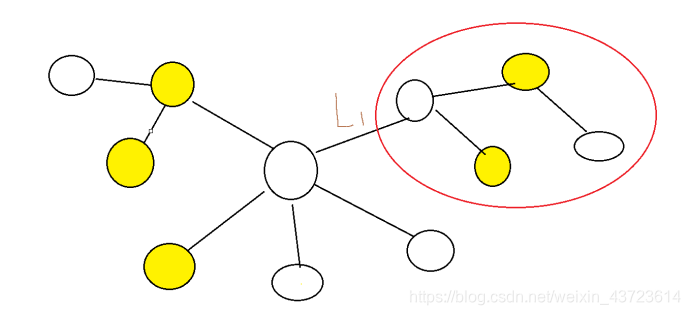要求距离和最短，对应程序设计算法一类的dp(动态规划)问题，通俗易懂解释就是用一个表(实现的方式根据题目而定)来记录所有已解的子问题的答案。相比于穷尽法，dp可以获取每个子策略的最优解，因为一个最优化策略的子策略总是最优的。此题分析可知是一棵无向树，所以我们可以考虑树状的动态规划求解。

3. 具体实现 (以java为示例,下文附带c++代码)

1. 总体思路:
   （1）设定dp[point][i] (在point结点选择i个重要节点的最佳解)
   （2）利用深度搜索到节点的子树底部(叶节点)，更新dp数组。
   （3）递归向上合并，直至还原最初题目抽象出来的无向树。
   （4）输出dp[root][k] (root为根节点)
2. 分点实现
   (1)自定义类Pair，成员包含node，weight，分别表示边的邻接边和边的权重。自定义类SideSet 成员为ArrayList。
   
   (2)输入部分可以使用java的ArrayList的一维数组来储存边与边之间的关系比较方便(c++的vector也可以实现)。因为ArrayList是一个可变长度的容器，在空间效率比普通数组有优势。比如下图，子树1与他的叶节点之间的关系可以表示为
   
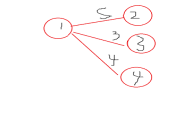
   SideSet[1].sideList.get(0) (side=2,weight=5)
   SideSet[1].sideList.get(1) (side=3,weight=3)
   SideSet[1].sideList.get(2) (side=4,weight=4)
   (3)定义find(int point,int father)函数深搜维护更新dp[][]数组。具体的dp数组最优解状态转移方程为
   
   point表示节点，sonTree表示在point的son子树下选择sonTree个重要节点，otherTree表示在已经更新的整棵树剔除son子树里面选择otherTree个重要节点。

(4)在更新的过程中利用一个临时的assist数组来保存更新数据，经过遍历所有可能后，利用assist[i]来维护更新dp[point][i]的最优解。

(5) 利用一个node[i]数组表示在i子树下有多少个重要节点，以此为for遍历边界进行更新。更新的时候要注意所选重要节点的数量不可以超过k。

4.算法效率分析

1.时间复杂度分析:
无向树的表示采用SideSet类与成员ArrayList表示的邻接表，在邻接表中进行dfs遍历的时间复杂度为O(n+e),n为节点个数，O(e)为查找邻接点的所需时间。
dp数组保存子树的信息，更新过程中结合dfs递归实现记忆化搜索。
如下图所示(node[i]表示i号子树下有多少个重要节点(node[i]<=k))

经过计算，在内部更新dp数组的关键代码时间复杂度是O(n),加上外部遍历每个子树的总子节点的时间复杂度不超过K*O(n)。
总结，加上dfs遍历的整个程序的总体时间复杂度O(n+e)*O(n)=O(n ^ 2+en)，即时间复杂度在O(n^2)附近。相比于暴力穷举，树状dp记忆化搜索很好地降低算法的时间复杂度。

2.空间复杂度分析:
本题做法在空间复杂度上面以题意要求的最大N,M,K来开出dp[N][K]进行记忆化搜索维护，有一定的以空间换时间的意思，在dp数组空间上可有待进行进一步的优化。以ArrayList邻接表表示的无向树则很好地利用java动态容器的特性来以最小空间保存无向树(c++的vector同理)。

5.算法附加功能

1.当根节点确定时,利用更新过程的node[k]数组保存k号子树下重要节点总数(含k)，可以求出任意节点的极大子树中含有重要节点数量。
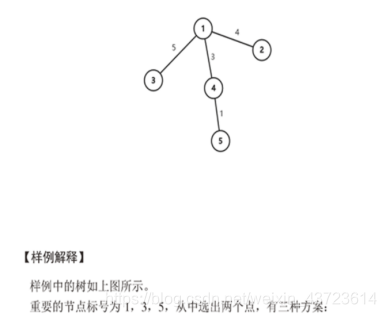
样例1:

样例2:

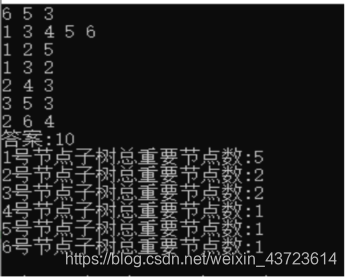
2.经过我们对无向树动态规划的研究，答案dp[root][k]的root节点不是唯一的，可以以任意一个节点为最初子树的root节点，然后利用深度搜索find()到最深的叶子节点，最后递归还原成原无向树。为说明这一点，我们采用最大编号节点作为root，代码一样通过ccf官网系统的评测。

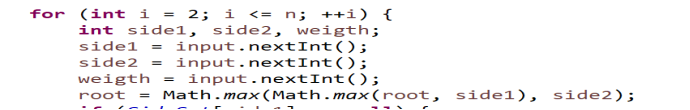
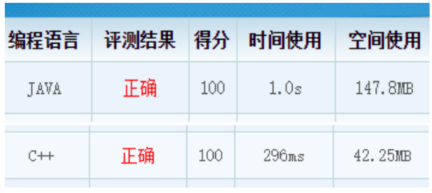
3.同样的dp算法思想，我们也用c++实现了，用c++的vector来实现无向树的存储，算法核心不变，只是在语法和细节上有所更改，一样通过ccf官网系统的评测。Java与c++在时间和空间上有所出入的主要原因由语言特性决定。

C++实现核心代码截图:

java与c++评测对比:

5.算法测试

样例测试:
1.

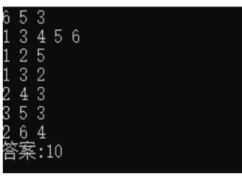
输入N=6,M=5,K=3(从6个点里面5个重要节点中选择3个重要节点)
最佳解:10
验证：选择1，3，5 三个节点，
1到3距离:2; 3到5距离:3; 1到5距离:5
最短距离=2+3+(2+3)=10
2.

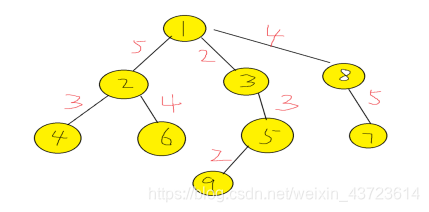
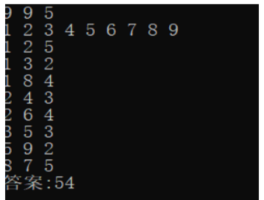
输入N=9,M=9,K=5(从9个点里面9个重要节点中选择5个重要节点)
最佳解:54
验证：选择1，3，5，8，9 五个节点，
1到8距离:4 3到8距离:6
5到8距离:9 9到8距离:11
3到1距离:2 5到1距离:5
9到1距离:7 5到3距离:3
9到3距离:5 9到5距离:2
最短距离=4+6+9+11+2+5+7+3+5+2=54

6.系统小结

1.通过本次系统题目的求解，学会了在树形结构下的动态规划算法。通过将题目抽象建模得到无向树，将题目转化成动态规划问题。
2.通过查阅资料，学习树状的动态规划用法，分析问题，进一步将题目转化成考虑子树节点对边的贡献，思考刻画状态转移方程，在具体的代码实现中需要考虑如何更新dp数组。在维护的过程中，需要临时assist数组来保存临时最小值，考虑时间复杂度和空间复杂度的优化，自定义Pair类数据结构来刻画边与边之间的关系等等，结合树形动态规划算法来求解问题。

参考文献
https://blog.csdn.net/Code92007/article/details/102022390

7.java源代码

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;

public class Main {
	final static int KMAX = 100;
	final static int SIZEMAX = 50001;
	final static long INF = 0x3f3f3f3f;
	static int k,n,m;
	static SideSet[] SideSet = new SideSet[SIZEMAX];
	static int[] node = new int[SIZEMAX];
	static long[] assist = new long[SIZEMAX];
	static long[][] dp = new long[SIZEMAX][KMAX];
	static int[] judge = new int[SIZEMAX];

	public static void main(String[] args) {
		initINF();
		int root = init_and_getRoot();
		find(root, 0);
		System.out.println(dp[root][k]);
		//附加功能:(root=1为例)输出i号节点下选择出j个重要节点的最短的距离和。
		//for(int i=1;i<n;i++){
		//	System.out.println(i+"号节点子树总重要结点数:"+node[i]);
		//}
	}

	static void initINF() {
		for (long[] ll : dp)
			Arrays.fill(ll, INF);
	}

	static void mark(int point) {
		dp[point][0] = 0;
		if (judge[point] == 1) {
			node[point] = 1;
			dp[point][1] = 0;
		}
	}
	
	static int init_and_getRoot() {
		int root = -1;
		Scanner input = new Scanner(System.in);
		n = input.nextInt();
		m = input.nextInt();
		k = input.nextInt();

		for (int i = 1; i <= m; ++i) {
			int side;
			side = input.nextInt();
			judge[side] = 1;
		}

		for (int i = 2; i <= n; ++i) {
			int side1, side2, weigth;
			side1 = input.nextInt();
			side2 = input.nextInt();
			weigth = input.nextInt();
			root = Math.max(Math.max(root, side1), side2);
			//以root为1作为例子测试附加功能,需要把init_and_getRoot()下面一行的root设为INF,然后注释上一行，打开下一行注释即可。
			//root = Math.min(Math.min(root, side1), side2);
			if (SideSet[side1] == null) {
				SideSet[side1] = new SideSet();
			}
			if (SideSet[side2] == null) {
				SideSet[side2] = new SideSet();
			}
			SideSet[side1].sideList.add(new Pair(side2, weigth));
			SideSet[side2].sideList.add(new Pair(side1, weigth));
		}
		return root;
	}

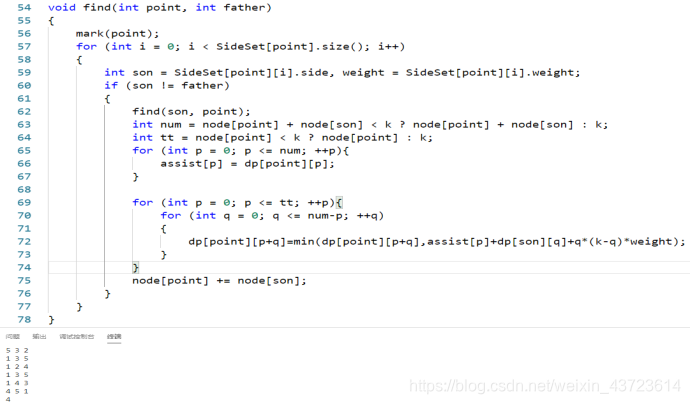
	static void find(int point, int father) {
		mark(point);
		for (int i = 0; i < SideSet[point].sideList.size(); i++) {
			int son = SideSet[point].sideList.get(i).side, weight = SideSet[point].sideList.get(i).weight;
			if (son != father) {
				find(son, point);
				int nSum = Math.min(node[point] + node[son], k);
				int nOther = Math.min(node[point], k);
				for (int j = 0; j <= nSum; ++j) {
					assist[j] = dp[point][j];
				}

				for (int otherTree = 0; otherTree <= nOther; otherTree++) {
					for (int sonTree = 0; sonTree <= nSum - otherTree; sonTree++) {
						dp[point][otherTree + sonTree] = Math.min(dp[point][otherTree + sonTree],
								assist[otherTree] + dp[son][sonTree] + sonTree * (k - sonTree) * weight);
					}
				}
				node[point] += node[son];
			}
		}
	}
}
class Pair {
	int side;
	int weight;
	public Pair(int side, int weight) {
		this.side = side;
		this.weight = weight;
	}
}
class SideSet {
	ArrayList<Pair> sideList = new ArrayList<Pair>();
}

8.c++源代码

#include <algorithm>
#include <iostream>
#include <string.h>
#include <vector>
using namespace std;
const int KMAX =  1e2 + 10;
const int SIZEMAX = 5e4 + 10;
const long long INF = 0x3f3f3f3f3f;

class Pair
{
public:
	int side;
	int weight;
	Pair(int x, int y) : side(x), weight(y) {}
};


std::vector<Pair> SideSet[SIZEMAX];
int node[SIZEMAX];
long long assist[SIZEMAX];
long long dp[SIZEMAX][KMAX];
int judge[SIZEMAX];
int k;

void input(){
	int n, m;
	cin >> n >> m >> k;
	memset(dp, INF, sizeof(dp));
	for (int i = 1; i <= m; ++i)
	{
		int side;
		cin >> side;
		judge[side] = 1;
	}
	for (int i = 2; i <= n; ++i)
	{
		int side1, side2, weigth;
		cin >> side1 >> side2 >> weigth;
		SideSet[side1].push_back(Pair(side2, weigth));
		SideSet[side2].push_back(Pair(side1, weigth));
	}
}
void mark(int point)
{
	dp[point][0] = 0;
	if (judge[point] == 1)
	{
		node[point] = 1;
		dp[point][1] = 0;
	}
}

void find(int point, int father)
{
	mark(point);
	for (int i = 0; i < SideSet[point].size(); i++)
	{
		int son = SideSet[point][i].side, weight = SideSet[point][i].weight;
		if (son != father)
		{
			find(son, point);
			int num = node[point] + node[son] < k ? node[point] + node[son] : k;
			int tt = node[point] < k ? node[point] : k;
			for (int p = 0; p <= num; ++p){
				assist[p] = dp[point][p];
			}
			
			for (int p = 0; p <= tt; ++p){
				for (int q = 0; q <= num-p; ++q)
				{
					dp[point][p+q]=min(dp[point][p+q],assist[p]+dp[son][q]+q*(k-q)*weight);
				}
			}
			node[point] += node[son];	
		}
	}
}
int main()
{
	input();
	find(1, -1);
	cout << dp[1][k];
	return 0;
}

// 6 5 3
// 1 3 4 5 6
// 1 2 5
// 1 3 2
// 2 4 3
// 3 5 3
// 4 6 4

/*
由题意知:一颗无向树,N个节点,N-1条边,任意两个节点都是连通的,所以任意两个节点都存在连通距离L(ij)（可经过别的节点）。
需要从其中规定的M个节点中选择出K个节点，使得K个节点间两两间的连通距离之和最短。
*/