基向量的转换
詹妮弗的基(列)向量所构成的矩阵
乘以她眼中的向量坐标得到我们眼中的向量坐标
这似乎是个拗口反向的过程因为矩阵实现的是从我的的网格到詹妮弗网格
但变换语言上又是由詹妮弗的语言描述转变为我们的描述。
但换个角度去想即可恍然大悟
这个过程可看作我们对詹妮弗向量的误解,即在我们坐标系中拥有相同
坐标的向量变换为她真正想表达的向量
大部分向量在某个变换中都会离开它原来张成的空间,不过,某些特殊向量留在了它们张成的空间里,意味着矩阵对他的作用仅仅是拉伸或者压缩而已。
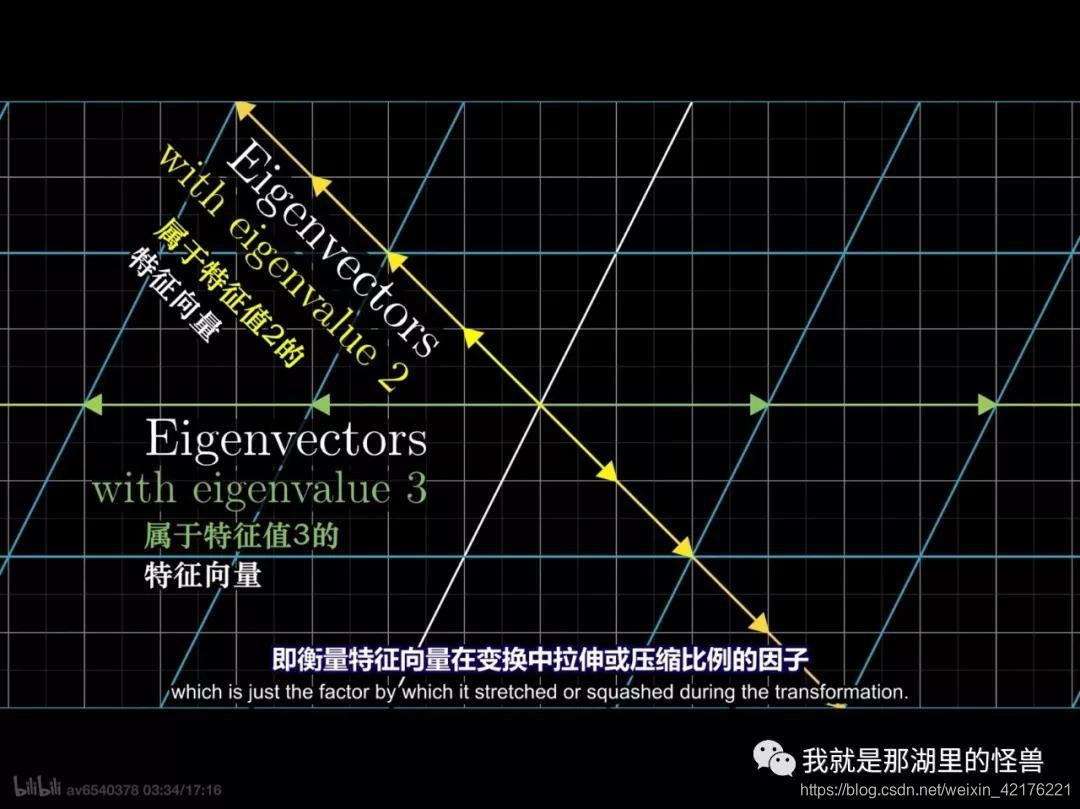
那么这样的向量就被称为特征向量,拉伸的值为其对应的特征矩阵
本性满足Av=λv,恒等变换后变为(A-λI)v=0。所以应寻找一个向量v,使得新矩阵具有非零解。
回顾:由于当且仅当矩阵所代表的变换将空间压缩到更低的维度时,才会存在一个非零向量,使得矩阵和它的乘积为零向量。而空间压缩对应的就是矩阵的行列式为零
所以det(A-λI)=0,也就意味着,我们的目标在于找到一个λ使得这个行列式为零,然后再找特征向量v。找到的v在A对应的变换中停留在它原来张成的线性空间中,并且拉伸的标量值为它所对应的λ值。
接下来是关于特征基的内容
如果基向量恰好是特征向量,把詹妮弗眼中的基向量作为矩阵的列。
对于对角矩阵的解读可以是:所有的基向量都是特征向量,对角元是他们所属的特征值。但这种矩阵毕竟是特例。
但如果是一个n个线性无关特征向量的n阶矩阵(即你能选出足够特征向量张成全空间的集合)
那么你就能变换坐标系,使特征向量就是基向量(这里作用的基变换的方法)
取出你想用作新基的向量的坐标(在这里指的是两个特征向量),然后讲坐标作为一个矩阵的列,这个列就是基变换矩阵。在右侧写下基变换矩阵,左侧写下基变换矩阵的逆,当你将原始的变换夹在两个矩阵中间时,所得的矩阵代表的是同一个变换,不过是从新基向量所构成的坐标系的角度来看的。

用特征向量完成这件事的意义在于
这个新矩阵必然是对角的,并且对角元为对应的特征值。
这是因为,它所处的坐标系的基向量在变换中只进行了缩放:
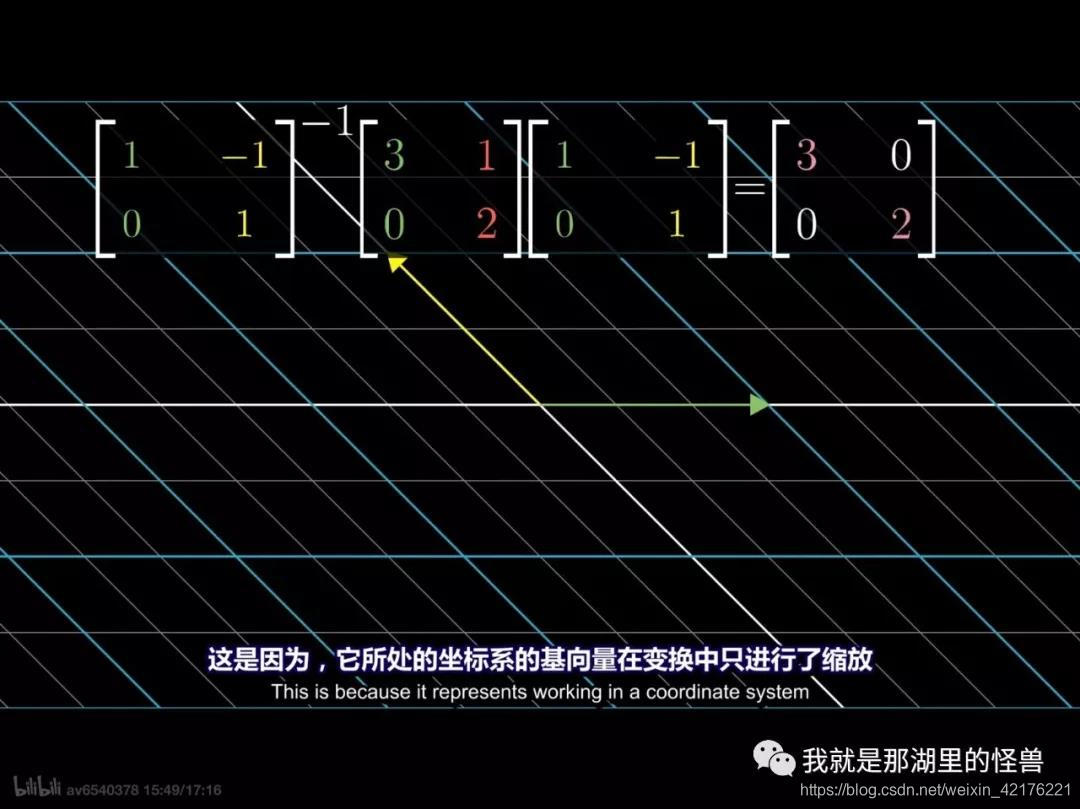
所以一组基向量(同时也是特征向量)构成的集合被称为特征基。
应用:如果要计算某个非特殊矩阵的100次幂,可以先变换得到特征基,在那个坐标系中计算100次幂,然后转换为标准坐标系
(即对角化)
但并不是所有的矩阵都可以相似对角化。
完结撒花
