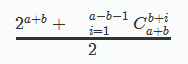洛谷P3726 [AH2017/HNOI2017]抛硬币

转载自：链接

题目描述

小 A 和小 B 是一对好朋友，他们经常一起愉快的玩耍。最近小 B 沉迷于**师手游，天天刷本，根本无心搞学习。但是已经入坑了几个月，却一次都没有抽到 SSR，让他非常怀疑人生。勤勉的小 A 为了劝说小 B 早日脱坑，认真学习，决定以抛硬币的形式让小 B 明白他是一个彻彻底底的非洲人，从而对这个游戏绝望。两个人同时抛 b 次硬币，如果小 A 的正面朝上的次数大于小 B 正面朝上的次数，则小 A 获胜。

但事实上，小 A 也曾经沉迷过拉拉游戏，而且他一次 UR 也没有抽到过，所以他对于自己的运气也没有太大把握。所以他决定在小 B 没注意的时候作弊，悄悄地多抛几次硬币，当然，为了不让小 B 怀疑，他不会抛太多次。现在小 A 想问你，在多少种可能的情况下，他能够胜过小 B 呢？由于答案可能太大，所以你只需要输出答案在十进制表示下的最后 k 位即可。

输入输出格式

输入格式：

有多组数据，对于每组数据输入三个数a,b,k，分别代表小A抛硬币的次数，小B抛硬币的次数，以及最终答案保留多少位整数。

输出格式：

对于每组数据，输出一个数，表示最终答案的最后 k 位为多少，若不足 k 位以 0 补全。

输入输出样例

输入样例#1：

2 1 9
3 2 1

输出样例#1：

000000004
6

说明

对于第一组数据，当小A抛2次硬币，小B抛1次硬币时，共有4种方案使得小A正面朝上的次数比小B多。

(01,0), (10,0), (11,0), (11,1)

对于第二组数据，当小A抛3次硬币，小B抛2次硬币时，共有16种方案使得小A正面朝上的次数比小B多。

(001,00), (010,00), (100,00), (011,00), (101,00), (110,00), (111,00), (011,01), (101,01), (110,01),(111,01), (011,10), (101,10), (110,10), (111,10), (111,11).

数据范围

10%的数据满足a,b≤20；

30%的数据满足a,b≤100；

70%的数据满足a,b≤100000，其中有20%的数据满足a=b；

100%的数据满足 $1 \leq a, b \leq 1 0^15, b \leq a \leq b + 10000, 1 \leq k \leq 9$ ，数据组数小于等于10。

扩展Lucas+卡常。。。

1. 首先考虑a=b的情况，那么对于一种B获胜的方案序列（比如二人都抛3次，A第三次正面朝上，B第一次和第二次正面朝上，序列就是001110），将每一位都异或1，就变成了A获胜的，当然，还要减去平局， $2a+b−Ca+ba2\frac{2^{a+b}-C_{a+b}^a}{2}$

2. 考虑a>b的情况，同样，一种B获胜的方案序列每一位都异或1。不过，由于A同学可以抛的硬币数量比较多，所以可以凭数量取胜，还会出现方案序列是A获胜，将每一位异或1后还是A获胜的序列。这样的序列假设b正面朝上j次，a比b多正面朝上j次，就应该满足，种类数就是

那么我们可以这么看这个式子：我们在a+b个数组成的序列中选择 $b + j$ 个元素变成1，然后其中在前b个元素中的1的个数就正好能完成那个和有关的枚举。所以：

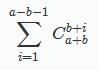
答案就是：

于是就用扩展Lucas算吧。

可是这题比较卡常。首先是要预处理阶乘。然后，在杨辉三角中，组合数具有对称性，所以计算组合数只用算一半。再加上标记处的优化，就能够通过这道题。

至于如何除以2，在扩展Lucas的计算过程中处理一下即可。

#include<iostream>
#include<algorithm>
#include<cstdio>
#define MOD 1000000007
using namespace std;
long long K,mod2,mod5,fac[2][2000010];
inline long long mexp(long long a,long long b,long long c){
    long long s=1;
    while(b){
        if(b&1)s=s*a%c;
        a=a*a%c;
        b>>=1;
    }
    return s;
}
void exgcd(long long a,long long b,long long &x,long long &y){
    if(!b){
        x=1;y=0;
        return;
    }
    exgcd(b,a%b,y,x);
    y-=a/b*x;
}
inline long long inv(long long a,long long c){
    if(!a)return 0;
    long long x=0,y=0;
    exgcd(a,c,x,y);
    return (x%c+c)%c;
}
inline long long mul(long long a,long long p,long long k){
    if(!a)return 1;
    long long s=fac[p!=2][k];
    s=mexp(s,a/k,k)*fac[p!=2][a%k]%k;
    return s*mul(a/p,p,k)%k;
}
long long C(long long n,long long m,long long mod,long long p,long long k,bool flag){
    if(n<m)return 0;
	long long q=0,s;
    for(long long i=n;i;i/=p)q+=i/p;
    for(long long i=m;i;i/=p)q-=i/p;
    for(long long i=n-m;i;i/=p)q-=i/p;
    if(p==2&&flag)q--;
    if(q>K)return 0;
    long long a=mul(n,p,k),b=mul(m,p,k),c=mul(n-m,p,k);
    s=a*inv(b,k)%k*inv(c,k)%k*mexp(p,q,k)%k;
    if(p==5&&flag)s=s*inv(2,k)%k;
    return s*(mod/k)%mod*inv(mod/k,k)%mod;
}
inline long long lucas(long long n,long long m,long long mod,bool flag){
    long long s=(C(n,m,mod,2,mod2,flag)+C(n,m,mod,5,mod5,flag))%mod;
    return s;
}
inline void init(long long a,long long b){
    int k=(a==2?0:1);
    fac[k][0]=1;
    for(int i=1;i<=b;i++){
        if(i%a)fac[k][i]=fac[k][i-1]*i%b;
        else fac[k][i]=fac[k][i-1];
    }
}
int main(){
    long long n,m;
    init(2,512);init(5,1953125);
    while(~scanf("%lld%lld%lld",&n,&m,&K)){
        long long ans,mod=mexp(10,K,MOD);
        mod2=mexp(2,K,MOD);mod5=mexp(5,K,MOD);
        if(n==m)ans=(mexp(2,n+m-1,mod)-lucas(n<<1,n,mod,true)+mod)%mod;
        else{
            ans=mexp(2,n+m-1,mod);
            for(long long i=(n+m)/2+1;i<n;i++){
				ans+=lucas(n+m,i,mod,false);
				ans%=mod;
			}
            if((n+m)%2==0){
				ans+=lucas(n+m,(n+m)/2,mod,true);
				ans%=mod;
			}
        }
        while(ans<mod/10){
            printf("0");
            mod/=10;
        }
        printf("%lld\n",ans);
    }
    return 0;
}