PCA背景简介
在许多领域的数据的分析和处理中,往往会有许多复杂的变量,变量与变量之间通常还存在着相关性,要从大量的变量中提取出能反映事物特征的信息是极其困难的,对单个的变量分析不全面,并且会损失信息,造成错误的结论。主成分分析(PCA)便是通过数学降维,找出最能决定数据特性的主元成分的数据分析方法,用较少的综合指标,揭示隐藏在多维复杂数据变量背后的简单结构,得到更为科学有效的数据信息。
PCA降维
PCA降维的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。
对于主成分坐标轴的选择,有两个要求:一是要相互正交,即基向量线性无关;二是要选取方差最大的方向,以实现数据在坐标轴上分散开来,便于观测。第一个坐标轴是原始数据中方差最大的方向,第二个坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的,第三个轴是与第1,2个轴正交的平面中方差最大的。通过这种方式可以得到n个这样的坐标轴。我们从这样的坐标轴中选出k个含有最大信息的坐标轴,便实现了降维处理。
具体实现方法
1. 协方差矩阵
对于我们得到的一组数据,可以求出其样本均值
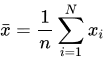
样本方差:
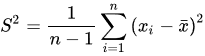
两个样本之间的协方差:
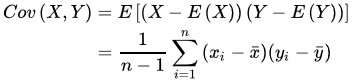
当协方差为0时,说明X和Y变量之间是线性无关的。
由所有的样本的列向量组成的矩阵X,根据
 可以得到两两数据之间的协方差矩阵:
可以得到两两数据之间的协方差矩阵:
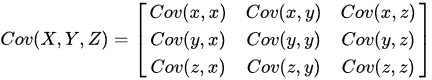
由矩阵可知,协方差矩阵为对称矩阵,对角线上为样本的方差,其他为两两变量之间的协方差,我们便可以利用对称矩阵的对角化将协方差化为0,实现变量间的线性无关。
2.特征值与特征向量
根据协方差矩阵计算其特征值与特征向量,由线性代数我们知道,如果一个向量v是矩阵A的特征向量,将一定可以表示成下面的形式:
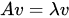
从而利用 |λE - A| = 0可解出矩阵的特征值,一个特征值便对应一组特征向量,特征向量之间是相互正交的。将所得到的特征向量对应其特征值从大到小排列,选出最大的k个向量单位化,便可作为PCA变换所需要的k个基向量,且方差最大。
3.基向量变换
X是一个mxn 的矩阵,它的每一个列向量都表示一个采样点上的数据 。Y 表示转换以后的新的数据集表示。 P是他们之间的线性转换,即计算向量内积。可表示为:
Y=PX
P便是由基向量组成的变换矩阵,经过线性转换,X的坐标便转换到新的基向量所决定的空间中的坐标Y,从几何上看,Y是X在新的空间中的投影。
经过基向量变换,即完成了数据的降维。
实例分析
以这样一组二维数据为例
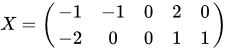
我们要把它降到一维,两组行向量的均值都为零,故不需要零均值中心化。
求协方差矩阵:
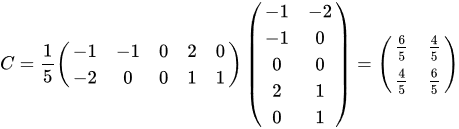
再根据所求的协方差矩阵计算其特征值与特征向量,求解得特征值为:
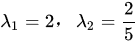
对应的特征向量为:

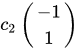
将特征向量单位化得到:
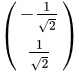
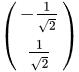
故基向量变换矩阵为:
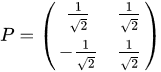
最后利用P与矩阵X做向量内积,便得到降维后的矩阵Y:

N维的数据矩阵也可以此类推,在得到k维降维后的向量之后,通常取2-3维作为主成分坐标,便可反映绝大部分的特征信息。
Matlab代码如下:
clear;
clc;
k = 1;
A = [-1 -1 0 2 0;
-2 0 0 1 1 ]’
[rows cols] = size(A)
covA = cov(A) %求样本的协方差矩阵
[vec val] = eigs(covA) %协方差矩阵的特征值D和特征向量V
meanA = mean(A) %样本均值mean
SCORE2 = (A - tempA)*vec %降到1维后得到的的主成分
pcaData2 = SCORE2(:,1:k) %取第一组数据
figure;
scatter(pcaData2(:,1));
