四叉树空间索引原理及其实现

前序

四叉树或四元树也被称为Q树（Q-Tree）。四叉树广泛应用于图像处理、空间数据索引、2D中的快速碰撞检测、存储稀疏数据等，而八叉树（Octree）主要应用于3D图形处理。对游戏编程，这会很有用。本文着重于对四叉树与八叉树的原理与结构的介绍，帮助您在脑海中建立四叉树与八叉树的基本思想。本文并不对这两种数据结构同时进行详解，而只对四叉树进行详解，因为八叉树的建立可由四叉树的建立推得。若有不足之处，望能不吝指出，以改进之。^_^  欢迎Email：[email protected]

四叉树与八叉树的结构与原理

四叉树（Q-Tree）是一种树形数据结构。四叉树的定义是：它的每个节点下至多可以有四个子节点，通常把一部分二维空间细分为四个象限或区域并把该区域里的相关信息存入到四叉树节点中。这个区域可以是正方形、矩形或是任意形状。以下为四叉树的二维空间结构(左)和存储结构(右)示意图（注意节点颜色与网格边框颜色）： 

四叉树的每一个节点代表一个矩形区域（如上图黑色的根节点代表最外围黑色边框的矩形区域），每一个矩形区域又可划分为四个小矩形区域，这四个小矩形区域作为四个子节点所代表的矩形区域。
较之四叉树，八叉树将场景从二维空间延伸到了三维空间。八叉树（Octree）的定义是：若不为空树的话，树中任一节点的子节点恰好只会有八个，或零个，也就是子节点不会有0与8以外的数目。那么，这要用来做什么？想象一个立方体，我们最少可以切成多少个相同等分的小立方体？答案就是8个。如下八叉树的结构示意图所示：

四叉树存储结构的c语言描述：

1. /* 一个矩形区域的象限划分：: 
2.            
3.        UL(1)   |    UR(0) 
4.      ----------|----------- 
5.        LL(2)   |    LR(3) 
6. 以下对该象限类型的枚举 
7. */  
8. typedef enum  
9. {  
10.     UR = 0,  
11.     UL = 1,  
12.     LL = 2,  
13.     LR = 3  
14. }QuadrantEnum;  
15.   
16. /* 矩形结构 */  
17. typedef struct quadrect_t  
18. {      
19.     double  left,   
20.             top,   
21.             right,   
22.             bottom;  
23. }quadrect_t;  
24.   
25. /* 四叉树节点类型结构 */  
26. typedef struct quadnode_t  
27. {  
28.     quadrect_t    rect;          //节点所代表的矩形区域  
29.     list_t        *lst_object;   //节点数据, 节点类型一般为链表，可存储多个对象  
30.     struct  quadnode_t  *sub[4]; //指向节点的四个孩子   
31. }quadnode_t;  
32.   
33. /* 四叉树类型结构 */  
34. typedef struct quadtree_t  
35. {  
36.     quadnode_t  *root;  
37.     int         depth;           // 四叉树的深度                      
38. }quadtree_t;  
39. 
    

四叉树的建立
1、利用四叉树分网格，如本文的第一张图<四层完全四叉树结构示意图>，根据左图的网格图形建立如右图所示的完全四叉树。
伪码：
Funtion QuadTreeBuild ( depth, rect )
{
QuadTree->depth = depth;
/*创建分支，root树的根，depth深度，rect根节点代表的矩形区域*/
QuadCreateBranch (  root, depth, rect );

}

Funtion QuadCreateBranch ( n, depth,rect )
{
  if ( depth!=0 )
  {
    n = new node;    //开辟新节点
     n ->rect = rect; //将该节点所代表的矩形区域存储到该节点中
     //将rect划成四份 rect[UR], rect[UL], rect[LL], rect[LR];
    /*创建各孩子分支*/
    QuadCreateBranch ( n->sub[UR], depth-1, rect [UR] );
    QuadCreateBranch ( n->sub[UL], depth-1, rect [UL] );
    QuadCreateBranch ( n->sub[LL], depth-1, rect [LL] );
    QuadCreateBranch ( n->sub[LR], depth-1, rect [LR] );
  }
}

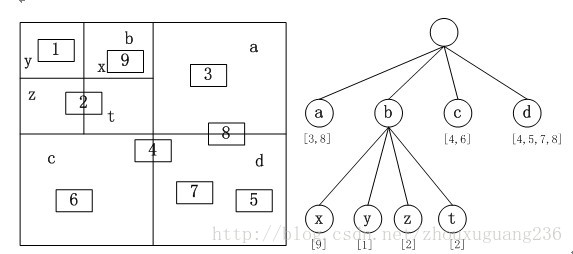
2、假设在一个矩形区域里有N个对象，如下左图一个黑点代表一个对象，每个对象的坐标位置都是已知的，用四叉树的一个节点存储一个对象，构建成如下右图所示的四叉树。

方法也是采用递归的方法对该矩形进行划分分区块，分完后再往里分，直到每一个子矩形区域里只包含一个对象为止。

伪码：
Funtion QuadtreeBuild()
{
  Quadtree = {empty}；
  For (i = 1;i<n;i++)      //遍历所有对象
  {
   QuadInsert(i, root)；//将i对象插入四叉树
  }          
   剔除多余的节点；  //执行完上面循环后，四叉树中可能有数据为空的叶子节点需要剔除

 }    

Funtion QuadInsert(i,n)      //该函数插入后四叉树中的每个节点所存储的对象数量不是1就是0
{  
  if（节点n有孩子）
  {      
  通过划分区域判断i应该放置于n节点的哪一个孩子节点c；       
  QuadInsert(i,c)；
  }
  else if（节点n存储了一个对象）
  {
    为n节点创建四个孩子；
    将n节点中的对象移到它应该放置的孩子节点中；
    通过划分区域判断i应该放置于n节点的哪一个孩子节点c；
    QuadInsert(i,c)；
  }
  else if（n节点数据为空）    
  {
    将i存储到节点n中；
  }
} 

（以上两种建立方法作为举一反三之用）

用四叉树查找某一对象

1、采用盲目搜索，与二叉树的递归遍历类似，可采用后序遍历或前序遍历或中序遍历对其进行搜索某一对象，时间复杂度为O（n）。

 2、根据对象在区域里的位置来搜索，采用分而治之思想，时间复杂度只与四叉树的深度有关。比起盲目搜索，这种搜索在区域里的对象越多时效果越明显

伪码：
Funtion find ( n, pos, )
{
      If (n节点所存的对象位置为 pos所指的位置 )
          Return n;
      If ( pos位于第一象限 )
          temp = find ( n->sub[UR], pos );
      else if ( pos位于第二象限)
          temp = find ( n->sub[UL], pos );
      else if ( pos位于第三象限 )
          temp = find ( n->sub[LL], pos );
      else  //pos 位于第四象限
          temp = find ( n->sub[LR], pos );
      return temp;   
  } 
  
结语：
熟话说：结构之法，算法之道。多一种数据结构就多一种解决问题的方法，多一种方法就多一种思维模式。

声明：版权所有，转载出处： http://blog.csdn.net/zhanxinhang/article/details/6706217

声明：版权所有，转载出处：http://blog.jobbole.com/81106/

参考：维基百科、百度百科

参考：CS267: Lecture 24, Apr 11 1996 Fast Hierarchical Methods for the N-body Problem, Part 1

用四叉树和希尔伯特曲线做空间索引

随着越来越多的数据和应用和地理空间相关，空间索引变得愈加重要。然而，有效地查询地理空间数据是相当大的挑战，因为数据是二维的（有时候更高），不能用标准的索引技术来查询位置。空间索引通过各种各样的技术来解决这个问题。在这篇博文中，我将介绍几种：四叉树，geohash（不要和geohashing混淆）以及空间填充曲线，并揭示它们是怎样相互关联的。

四叉树

四叉树是种很直接的空间索引技术。在四叉树中，每个节点表示覆盖了部分进行索引的空间的边界框，根节点覆盖了整个区域。每个节点要么是叶节点，有包含一个或多个索引点的列表，没有孩子。要么是内部节点，有四个孩子，每个孩子对应将区域沿两根轴对半分得到的四个象限中的一个，四叉树也因此得名。

图1    展示四叉树是怎样划分索引区域的 来源：维基百科

将数据插入四叉树很简单：从根节点开始，判断你的数据点属于哪个象限。递归到相应的节点，重复步骤，直到到达叶节点，然后将该点加入节点的索引点列表中。如果列表中的元素个数超出了预设的最大数目，则将节点分裂，将其中的索引点移动到相应的子节点中去。

图2    四叉树的内部结构

查询四叉树时从根节点开始，检查每个子节点看是否与查询的区域相交。如果是，则递归进入该子节点。当到达叶节点时，检查点列表中的每一个项看是否与查询区域相交，如果是则返回此项。

注意四叉树是非常规则的，事实上它是一种字典树，因为树节点的值不依赖于插入的数据。因此我们可以用直接的方式给节点编号：用二进制给每个象限编号（左上是00，右上是10等等 译者注：第一个比特位为0表示在左半平面，为1在右半平面。第二个比特位为0表示在上半平面，为1在下半平面），任一节点的编号是由从根开始，它的各祖先的象限号码串接而成的。在这个编号系统中，图2中右下角节点的编号是1101。

如果我们定义了树的最大深度，不需通过树就可以计算数据点所在节点的编号：只要把节点的坐标标准化到适当的整数区间中（比如32位整数），然后把转化后x, y坐标的比特位交错组合。每对比特指定了假想的四叉树中的一个象限。（译者注：不了解的读者可看看Z-order，它和下文的希尔伯特曲线都是将二维的点映射到一维的方法）

Geohash

上述编号系统可能看起来有些熟悉，没错，就是geohash！此刻，你可以把四叉树扔掉了。节点编号，或者说geohash，包含了对于节点在树中位置我们需要的全部信息。全高树中的每个叶节点是个完整的geohash，每个内部节点代表从它最小的叶节点到最大的叶节点的区间。因此，通过查询所需的节点覆盖的数值区间中的一切（在geohash上索引），你可以有效地定位任意内部节点下的所有数据点。

一旦我们丢掉了四叉树，查询就变得复杂一点了。我们需要事先构建搜索集合而不是在树中递归地精炼搜索集合。首先，找到完全覆盖查询区域的最小前缀（或者说四叉树节点  译者注：注意在我们的编号系统中节点由比特串表示）。在最坏情况下，这可能远大于实际的查询区域，比如对于在索引区域中心、和四个象限都相交的小块地方，查询将要从根节点开始。

现在的目标是构建一组完全包含查询区域的前缀，并且尽可能少包含区域外的部分。如果没有其他约束，我们可以简单地选择与查询区域相交的叶节点，但这会造成大量的查询。所以要加一个约束：使得要查询的不同区间最少。

一种达到这个目的的方法是先设置我们愿意承受的查询区间的最大数目。构建一组区间，最开始都设为我们之前指定的前缀。从中选择可以再分裂而不超出最大区间数并将从查询区域删除最不受欢迎区域的节点。重复这个过程直到集合中再没有区间可以细分。最后，检查得到的集合，如果可能的话合并相邻的区间。下面的图说明了这对于查询一个圆形区域且限制最大5个查询区间是如何工作的。

图3    一个对区域的查询是怎样分解成一连串geohash前缀/区间的

这个方法工作地很好，它使我们避免了递归查找。我们执行的一整套区间查找都可以并行完成。由于每次查找都预期要一次硬盘搜索，将查询并行化大大减少了返回结果需要的时间。

然而，我们还可以做得更好。你可能注意到上图中我们要查询的所有区域都是相邻的，但我们却只能将其中两个合并（选择区域的右下角的两个）成一个单独的查询，进而只要4次单独查询。（译者注：这两个区域可以合并是因为它们在geohash以Z字形遍历区域的路径上是相邻的）这个后果部分是由于geohash访问子区域的顺序，在每个象限中从左到右，从上到下。从右上角象限到左下角象限的不连续性使得我们不得不将本可以使之连续的区间分裂。如果以不同的顺序访问区域，可能我们就可以最小化或者消除这些不连续性，使得更多的区域可以被看做是相邻的，一次查询就可得到结果。通过这样效率上的提升，对于同样的覆盖区域，我们可以做更少的查询，或者相反地，同样的查询次数的情况下包含更少的无关区域。

图4    geohash访问象限的顺序

希尔伯特曲线

现在假设我们以U字形来访问区域。在每个象限中，我们同样以U字形来访问子象限，但是要调整好U字形的朝向使得和相邻的象限衔接起来。如果我们正确地组织了这些U字形的朝向，我们就能完全消除不连续性，不管我们选择了什么分辨率，都能连续地访问整个区域，可以在完全地探访了一个区域后才移动到下一个。这个方案不仅消除了不连续性，而且提高了总体的局域性。按照这个方案得到的图案看起来有些熟悉，没错，就是希尔伯特曲线。

希尔伯特曲线属于一类被称为空间填充曲线的一维分形，因为它们虽然是一维的线，却可以填充固定区域的所有空间。它们相当有名，部分是由于XKCD把它们用于互联网地图。如你所见，对于空间索引它们也是有用的，因为它们展现的正是我们需要的局域性和连续性。再看看之前用一组查询来覆盖圆的例子，我们发现（应用希尔伯特曲线）还可以减少一次查询：左下方的小区域现在和它右边的区域连起来了（减少一次），虽然底部的两块区域不再连续了（增加一次），右下角的区域现在却和它上方的连续了（减少一次）。

图5    希尔伯特曲线访问象限的顺序

到目前为止，我们优雅的系统还缺一样东西：将(x,y)坐标转换为希尔伯特曲线上相应位置的方法。对于geohash，这是简单而明显的–只需将x, y坐标交错，但没有明显的方法修改这个方案使之对希尔伯特曲线也适用。在网上搜索，你很可能遇到很多关于希尔伯特曲线是怎样画出来的描述，但很少有关于找到任意点（在曲线上）位置的。为了搞定它，我们需要更仔细看看希尔伯特曲线是怎么递归构建的。

首先要注意到虽然大多数关于希尔伯特曲线的文献都关注曲线是怎么画出来的，却容易让我们忽略曲线的本质属性以及其重要性：曲线规定了平面上点的顺序。如果我们用这顺序来表达希尔伯特曲线，画曲线就不值一提了：仅仅是把点连起来。忘记怎么把子曲线连起来吧，把注意力集中在怎么递归地列举点上。

图6    希尔伯特曲线规定了二维平面上的点的顺序

在根这一层，列举点很简单：选定一个方向和一个起始点，环绕四个象限，用0到3给他们编号。当我们要确定访问子象限的顺序同时维护总体的邻接属性，困难就来了。通过检查我们发现，子象限的曲线是原曲线的简单变换，而且只有四种变换。自然地，这个结论也适用于子子象限，等等。对于一个给定的象限，我们在其中画出的曲线是由象限所在大的方形的曲线以及该象限的位置决定的。只需要费一点力，我们就能构建出如下概况所有情况的表。

图7

假设我们想用这个表来确定某个点在第三层希尔伯特曲线上的位置。在这个例子中，假设点的坐标是(5,2)。（译者注：请参照图8）从上图的第一个方形开始，找到你的点所在的象限。在这个例子中，是在右上方的象限。那么点在希尔伯特曲线上的位置的第一部分是3（二进制是11）。接着我们进入象限3里面的方块，在这个例子中，它是（图7中的）第二个方块。重复刚才的过程：我们的点落在哪个子象限？这次是左下角，意味着位置的下一部分是1（二进制01），我们将进入的小方块又是第二个。最后一次重复这个过程，发现点落在右上角的子子象限，因此位置的最后部分是3（二进制11）。把这些位置连接起来，我们得到点在曲线上的位置是二进制的110111，或者十进制的55。

图8  三阶希尔伯特曲线

让我们更系统一些，写出从x, y坐标到希尔伯特曲线位置转换的方法。首先，我们要以计算机看得懂的形式表达图7：

1 2 3 4 5

hilbert_map = { 'a' : {( 0 , 0 ): ( 0 , 'd' ), ( 0 , 1 ): ( 1 , 'a' ), ( 1 , 0 ): ( 3 , 'b' ), ( 1 , 1 ): ( 2 , 'a' )}, 'b' : {( 0 , 0 ): ( 2 , 'b' ), ( 0 , 1 ): ( 1 , 'b' ), ( 1 , 0 ): ( 3 , 'a' ), ( 1 , 1 ): ( 0 , 'c' )}, 'c' : {( 0 , 0 ): ( 2 , 'c' ), ( 0 , 1 ): ( 3 , 'd' ), ( 1 , 0 ): ( 1 , 'c' ), ( 1 , 1 ): ( 0 , 'b' )}, 'd' : {( 0 , 0 ): ( 0 , 'a' ), ( 0 , 1 ): ( 3 , 'c' ), ( 1 , 0 ): ( 1 , 'd' ), ( 1 , 1 ): ( 2 , 'd' )}}

上面的代码中，每个hilbert_map的元素对应图7四个方形中的一个。为了容易区分，我用一个字母来标识每个方块：’a'是第一个方块，’b'是第二个，等等。每个方块的值是个字典，将(子)象限的x, y坐标映射到曲线上的位置（元组值的第一部分）以及下一个用到的方块（元组值的第二部分）。下面的代码展示了怎么用这个来将x, y坐标转换成希尔伯特曲线上的位置：

1 2 3 4 5 6 7 8 9 10

def point_to_hilbert(x, y, order = 16 ):      current_square = 'a'      position = 0      for i in range (order - 1 , - 1 , - 1 ):          position << = 2          quad_x = 1 if x & ( 1 << i) else 0          quad_y = 1 if y & ( 1 << i) else 0          quad_position, current_square = hilbert_map[current_square][(quad_x, quad_y)]          position | = quad_position      return position

函数的输入是为整数的x, y坐标和曲线的阶。一阶曲线填充2×2的格子，二阶曲线填充4×4的格子，等等。我们的x, y坐标应该先标准化到0到2order-1的区间。这个函数从最高位开始，逐步处理x, y坐标的每个比特位。在每个阶段中，通过测试对应的比特位，可以确定坐标处于哪个（子）象限，还可以从我们之前定义的hilbert_map中取得在曲线上的位置以及下一个要用的方块。在这阶段取得的位置，加入到目前总的位置的最低两位。在下一次循环的开头，总的位置左移两位以便给下一个位置腾出地方。

让我们运行一下之前的例子来检验一下函数写对了没有：

1 2	>>> point_to_hilbert( 5 , 2 , 3 ) 55

对了！为了进一步测试，我们可以用这个函数生成一条希尔伯特曲线的有序点的完整列表，然后用电子制表软件把它们画出来看我们是否真的得到了一条希尔伯特曲线。在Python交互解释器中输入如下代码：

1 2 3

>>> points = [(x, y) for x in range ( 8 ) for y in range ( 8 )] >>> sorted_points = sorted (points, key = lambda k: point_to_hilbert(k[ 0 ], k[ 1 ], 3 )) >>> print 'n' .join( '%s,%s' % x for x in sorted_points)

将输出的文本粘贴到文件中，保存为hilbert.csv，用你最喜欢的电子制表软件打开，将数据画成一个散点图。结果当然是一条漂亮的希尔伯特曲线！

将hilbert_map做简单的反转就能实现point_to_hilbert的逆向功能（将希尔伯特曲线上的位置转换为x, y坐标），把这个留给读者作为练习吧。

结论

空间索引，从四叉树到geohash到希尔伯特曲线，到这就结束了。最后一点说明：如果你将一条希尔伯特曲线上的x, y坐标的有序序列写成二进制形式，对于顺序你注意到什么有趣的东西吗？你想到了什么？

结束前的一点警告：我在这里描述的全部索引方法都只适用于索引点。如果你想索引线、折线或者多边形，这些方法可能就不管用了。据我所知，已知的唯一能有效索引形体的算法是R-tree，这是一种完全不同且更复杂的方法。

四叉树空间索引原理及其实现

四叉树索引的基本思想是将地理空间递归划分为不同层次的树结构。它将已知范围的空间等分成四个相等的子空间，如此递归下去，直至树的层次达到一定深度或者满足某种要求后停止分割。四叉树的结构比较简单，并且当空间数据对象分布比较均匀时，具有比较高的空间数据插入和查询效率，因此四叉树是GIS中常用的空间索引之一。常规四叉树的结构如图所示，地理空间对象都存储在叶子节点上，中间节点以及根节点不存储地理空间对象。

 

四叉树示意图

       四叉树对于区域查询，效率比较高。但如果空间对象分布不均匀，随着地理空间对象的不断插入，四叉树的层次会不断地加深，将形成一棵严重不平衡的四叉树，那么每次查询的深度将大大的增多，从而导致查询效率的急剧下降。

本节将介绍一种改进的四叉树索引结构。四叉树结构是自顶向下逐步划分的一种树状的层次结构。传统的四叉树索引存在着以下几个缺点：

(1)空间实体只能存储在叶子节点中，中间节点以及根节点不能存储空间实体信息，随着空间对象的不断插入，最终会导致四叉树树的层次比较深，在进行空间数据窗口查询的时候效率会比较低下。

(2)同一个地理实体在四叉树的分裂过程中极有可能存储在多个节点中，这样就导致了索引存储空间的浪费。

(3)由于地理空间对象可能分布不均衡，这样会导致常规四叉树生成一棵极为不平衡的树，这样也会造成树结构的不平衡以及存储空间的浪费。

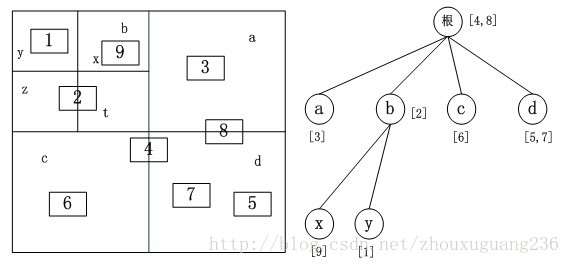
相应的改进方法，将地理实体信息存储在完全包含它的最小矩形节点中，不存储在它的父节点中，每个地理实体只在树中存储一次，避免存储空间的浪费。首先生成满四叉树，避免在地理实体插入时需要重新分配内存，加快插入的速度，最后将空的节点所占内存空间释放掉。改进后的四叉树结构如下图所示。四叉树的深度一般取经验值4-7之间为最佳。

 

图改进的四叉树结构

为了维护空间索引与对存储在文件或数据库中的空间数据的一致性，作者设计了如下的数据结构支持四叉树的操作。

(1)四分区域标识

分别定义了一个平面区域的四个子区域索引号，右上为第一象限0，左上为第二象限1，左下为第三象限2，右下为第四象限3。

typedef enum

{

      UR = 0,// UR第一象限

      UL = 1, // UL为第二象限

      LL = 2, // LL为第三象限

      LR = 3  // LR为第四象限

}QuadrantEnum;

(2)空间对象数据结构

空间对象数据结构是对地理空间对象的近似，在空间索引中，相当一部分都是采用MBR作为近似。

/*空间对象MBR信息*/

typedef struct SHPMBRInfo

{

      int nID;       //空间对象ID号

      MapRect Box;    //空间对象MBR范围坐标

}SHPMBRInfo;

nID是空间对象的标识号，Box是空间对象的最小外包矩形（MBR）。

(3)四叉树节点数据结构

四叉树节点是四叉树结构的主要组成部分，主要用于存储空间对象的标识号和MBR，也是四叉树算法操作的主要部分。

/*四叉树节点类型结构*/

typedef struct QuadNode

{

      MapRect            Box;                   //节点所代表的矩形区域

      int                nShpCount;        //节点所包含的所有空间对象个数

      SHPMBRInfo* pShapeObj;          //空间对象指针数组

      int         nChildCount;            //子节点个数

      QuadNode *children[4];             //指向节点的四个孩子

}QuadNode;

Box是代表四叉树对应区域的最小外包矩形，上一层的节点的最小外包矩形包含下一层最小外包矩形区域；nShpCount代表本节点包含的空间对象的个数；pShapeObj代表指向空间对象存储地址的首地址，同一个节点的空间对象在内存中连续存储；nChildCount代表节点拥有的子节点的数目；children是指向孩子节点指针的数组。

上述理论部分都都讲的差不多了，下面就贴上我的C语言实现版本代码。

头文件如下：

#ifndef __QUADTREE_H_59CAE94A_E937_42AD_AA27_794E467715BB__
#define __QUADTREE_H_59CAE94A_E937_42AD_AA27_794E467715BB__

/* 一个矩形区域的象限划分：:

UL(1)   |    UR(0)
----------|-----------
LL(2)   |    LR(3)
以下对该象限类型的枚举
*/
typedef enum
{
UR = 0,
UL = 1,
LL = 2,
LR = 3
}QuadrantEnum;

/*空间对象MBR信息*/
typedef struct SHPMBRInfo
{
int nID; //空间对象ID号
MapRect Box; //空间对象MBR范围坐标

}SHPMBRInfo;

/* 四叉树节点类型结构 */
typedef struct QuadNode
{
MapRect Box; //节点所代表的矩形区域
int nShpCount; //节点所包含的所有空间对象个数
SHPMBRInfo* pShapeObj; //空间对象指针数组
int nChildCount; //子节点个数
QuadNode  *children[4]; //指向节点的四个孩子 
}QuadNode;

/* 四叉树类型结构 */
typedef struct quadtree_t
{
QuadNode  *root;
int         depth;           // 四叉树的深度                    
}QuadTree;

//初始化四叉树节点

QuadNode *InitQuadNode();

//层次创建四叉树方法（满四叉树）
void CreateQuadTree(int depth,GeoLayer *poLayer,QuadTree* pQuadTree);

//创建各个分支
void CreateQuadBranch(int depth,MapRect &rect,QuadNode** node);

//构建四叉树空间索引
void BuildQuadTree(GeoLayer*poLayer,QuadTree* pQuadTree);

//四叉树索引查询(矩形查询)
void SearchQuadTree(QuadNode* node,MapRect &queryRect,vector<int>& ItemSearched);

//四叉树索引查询(矩形查询)并行查询
void SearchQuadTreePara(vector<QuadNode*> resNodes,MapRect &queryRect,vector<int>& ItemSearched);

//四叉树的查询（点查询）
void PtSearchQTree(QuadNode* node,double cx,double cy,vector<int>& ItemSearched);

//将指定的空间对象插入到四叉树中
void Insert(long key,MapRect &itemRect,QuadNode* pNode);

//将指定的空间对象插入到四叉树中
void InsertQuad(long key,MapRect &itemRect,QuadNode* pNode);

//将指定的空间对象插入到四叉树中
void InsertQuad2(long key,MapRect &itemRect,QuadNode* pNode);

//判断一个节点是否是叶子节点
bool IsQuadLeaf(QuadNode* node);

//删除多余的节点
bool DelFalseNode(QuadNode* node);

//四叉树遍历(所有要素)
void TraversalQuadTree(QuadNode* quadTree,vector<int>& resVec);

//四叉树遍历（所有节点）
void TraversalQuadTree(QuadNode* quadTree,vector<QuadNode*>& arrNode);

//释放树的内存空间
void ReleaseQuadTree(QuadNode** quadTree);

//计算四叉树所占的字节的大小
long CalByteQuadTree(QuadNode* quadTree,long& nSize);

#endif

源文件如下：

#include "QuadTree.h"

QuadNode *InitQuadNode()
{
QuadNode *node = new QuadNode;
node->Box.maxX = 0;
node->Box.maxY = 0;
node->Box.minX = 0;
node->Box.minY = 0;

for (int i = 0; i < 4; i ++)
{
node->children[i] = NULL;
}
node->nChildCount = 0;
node->nShpCount = 0;
node->pShapeObj = NULL;

return node;
}

void CreateQuadTree(int depth,GeoLayer *poLayer,QuadTree* pQuadTree)
{

pQuadTree->depth = depth;

GeoEnvelope env; //整个图层的MBR
poLayer->GetExtent(&env);

MapRect rect;
rect.minX = env.MinX;
rect.minY = env.MinY;
rect.maxX = env.MaxX;
rect.maxY = env.MaxY;
//创建各个分支

CreateQuadBranch(depth,rect,&(pQuadTree->root));

int nCount = poLayer->GetFeatureCount();
GeoFeature **pFeatureClass = new GeoFeature*[nCount];
for (int i = 0; i < poLayer->GetFeatureCount(); i ++)
{
pFeatureClass[i] = poLayer->GetFeature(i); 
}

//插入各个要素
GeoEnvelope envObj; //空间对象的MBR
//#pragma omp parallel for
for (int i = 0; i < nCount; i ++)
{
pFeatureClass[i]->GetGeometry()->getEnvelope(&envObj);
rect.minX = envObj.MinX;
rect.minY = envObj.MinY;
rect.maxX = envObj.MaxX;
rect.maxY = envObj.MaxY;
InsertQuad(i,rect,pQuadTree->root);
}

//DelFalseNode(pQuadTree->root);
}

void CreateQuadBranch(int depth,MapRect &rect,QuadNode** node)
{
if (depth != 0)
{
*node = InitQuadNode(); //创建树根
QuadNode *pNode = *node;
pNode->Box = rect;

pNode->nChildCount = 4;

MapRect boxs[4];
pNode->Box.Split(boxs,boxs+1,boxs+2,boxs+3);
for (int i = 0; i < 4; i ++)
{
//创建四个节点并插入相应的MBR
pNode->children[i] = InitQuadNode();
pNode->children[i]->Box = boxs[i];

CreateQuadBranch(depth-1,boxs[i],&(pNode->children[i]));
}
}
}

void BuildQuadTree(GeoLayer *poLayer,QuadTree* pQuadTree)
{
assert(poLayer);
GeoEnvelope env; //整个图层的MBR
poLayer->GetExtent(&env);
pQuadTree->root = InitQuadNode();

QuadNode* rootNode = pQuadTree->root;

rootNode->Box.minX = env.MinX;
rootNode->Box.minY = env.MinY;
rootNode->Box.maxX = env.MaxX;
rootNode->Box.maxY = env.MaxY;

//设置树的深度( 根据等比数列的求和公式)
//pQuadTree->depth = log(poLayer->GetFeatureCount()*3/8.0+1)/log(4.0);
int nCount = poLayer->GetFeatureCount();

MapRect rect;
GeoEnvelope envObj; //空间对象的MBR
for (int i = 0; i < nCount; i ++)
{
poLayer->GetFeature(i)->GetGeometry()->getEnvelope(&envObj);
rect.minX = envObj.MinX;
rect.minY = envObj.MinY;
rect.maxX = envObj.MaxX;
rect.maxY = envObj.MaxY;
InsertQuad2(i,rect,rootNode);
}

DelFalseNode(pQuadTree->root);
}

void SearchQuadTree(QuadNode* node,MapRect &queryRect,vector<int>& ItemSearched)
{
assert(node);

//int coreNum = omp_get_num_procs();
//vector<int> * pResArr = new vector<int>[coreNum];

if (NULL != node)
{
for (int i = 0; i < node->nShpCount; i ++)
{
if (queryRect.Contains(node->pShapeObj[i].Box)
|| queryRect.Intersects(node->pShapeObj[i].Box))
{
ItemSearched.push_back(node->pShapeObj[i].nID);
}
}

//并行搜索四个孩子节点
/*#pragma omp parallel sections
{
#pragma omp section
if ((node->children[0] != NULL) && 
(node->children[0]->Box.Contains(queryRect)
|| node->children[0]->Box.Intersects(queryRect)))
{
int tid = omp_get_thread_num();
SearchQuadTree(node->children[0],queryRect,pResArr[tid]);
}

#pragma omp section
if ((node->children[1] != NULL) && 
(node->children[1]->Box.Contains(queryRect)
|| node->children[1]->Box.Intersects(queryRect)))
{
int tid = omp_get_thread_num();
SearchQuadTree(node->children[1],queryRect,pResArr[tid]);
}

#pragma omp section
if ((node->children[2] != NULL) && 
(node->children[2]->Box.Contains(queryRect)
|| node->children[2]->Box.Intersects(queryRect)))
{
int tid = omp_get_thread_num();
SearchQuadTree(node->children[2],queryRect,pResArr[tid]);
}

#pragma omp section
if ((node->children[3] != NULL) && 
(node->children[3]->Box.Contains(queryRect)
|| node->children[3]->Box.Intersects(queryRect)))
{
int tid = omp_get_thread_num();
SearchQuadTree(node->children[3],queryRect,pResArr[tid]);
}
}*/
for (int i = 0; i < 4; i ++)
{
if ((node->children[i] != NULL) && 
(node->children[i]->Box.Contains(queryRect)
|| node->children[i]->Box.Intersects(queryRect)))
{
SearchQuadTree(node->children[i],queryRect,ItemSearched);
//node = node->children[i]; //非递归
}
}
}

/*for (int i = 0 ; i < coreNum; i ++)
{
ItemSearched.insert(ItemSearched.end(),pResArr[i].begin(),pResArr[i].end());
}*/

}

void SearchQuadTreePara(vector<QuadNode*> resNodes,MapRect &queryRect,vector<int>& ItemSearched)
{
int coreNum = omp_get_num_procs();
omp_set_num_threads(coreNum);
vector<int>* searchArrs = new vector<int>[coreNum];
for (int i = 0; i < coreNum; i ++)
{
searchArrs[i].clear();
}

#pragma omp parallel for
for (int i = 0; i < resNodes.size(); i ++)
{
int tid = omp_get_thread_num();
for (int j = 0; j < resNodes[i]->nShpCount; j ++)
{
if (queryRect.Contains(resNodes[i]->pShapeObj[j].Box)
|| queryRect.Intersects(resNodes[i]->pShapeObj[j].Box))
{
searchArrs[tid].push_back(resNodes[i]->pShapeObj[j].nID);
}
}
}

for (int i = 0; i < coreNum; i ++)
{
ItemSearched.insert(ItemSearched.end(),
searchArrs[i].begin(),searchArrs[i].end());
}

delete [] searchArrs;
searchArrs = NULL;
}

void PtSearchQTree(QuadNode* node,double cx,double cy,vector<int>& ItemSearched)
{
assert(node);
if (node->nShpCount >0) //节点   
{
for (int i = 0; i < node->nShpCount; i ++)
{
if (node->pShapeObj[i].Box.IsPointInRect(cx,cy))
{
ItemSearched.push_back(node->pShapeObj[i].nID);
}
}
}

else if (node->nChildCount >0) //节点
{
for (int i = 0; i < 4; i ++)
{
if (node->children[i]->Box.IsPointInRect(cx,cy))
{
PtSearchQTree(node->children[i],cx,cy,ItemSearched);
}
}
}

//找出重复元素的位置
sort(ItemSearched.begin(),ItemSearched.end()); //先排序,默认升序
vector<int>::iterator unique_iter = 
unique(ItemSearched.begin(),ItemSearched.end());
ItemSearched.erase(unique_iter,ItemSearched.end());
}

void Insert(long key, MapRect &itemRect,QuadNode* pNode)
{
QuadNode *node = pNode; //保留根节点副本
SHPMBRInfo pShpInfo;

//节点有孩子
if (0 < node->nChildCount)
{
for (int i = 0; i < 4; i ++)
{  
//如果包含或相交，则将节点插入到此节点
if (node->children[i]->Box.Contains(itemRect)
|| node->children[i]->Box.Intersects(itemRect))
{
//node = node->children[i];
Insert(key,itemRect,node->children[i]);
}
}
}

//如果当前节点存在一个子节点时
else if (1 == node->nShpCount)
{
MapRect boxs[4];
node->Box.Split(boxs,boxs+1,boxs+2,boxs+3);

//创建四个节点并插入相应的MBR
node->children[UR] = InitQuadNode();
node->children[UL] = InitQuadNode();
node->children[LL] = InitQuadNode();
node->children[LR] = InitQuadNode();

node->children[UR]->Box = boxs[0];
node->children[UL]->Box = boxs[1];
node->children[LL]->Box = boxs[2];
node->children[LR]->Box = boxs[3];
node->nChildCount = 4;

for (int i = 0; i < 4; i ++)
{  
//将当前节点中的要素移动到相应的子节点中
for (int j = 0; j < node->nShpCount; j ++)
{
if (node->children[i]->Box.Contains(node->pShapeObj[j].Box)
|| node->children[i]->Box.Intersects(node->pShapeObj[j].Box))
{
node->children[i]->nShpCount += 1;
node->children[i]->pShapeObj = 
(SHPMBRInfo*)malloc(node->children[i]->nShpCount*sizeof(SHPMBRInfo));

memcpy(node->children[i]->pShapeObj,&(node->pShapeObj[j]),sizeof(SHPMBRInfo));

free(node->pShapeObj);
node->pShapeObj = NULL;
node->nShpCount = 0;
}
}
}

for (int i = 0; i < 4; i ++)
{  
//如果包含或相交，则将节点插入到此节点
if (node->children[i]->Box.Contains(itemRect)
|| node->children[i]->Box.Intersects(itemRect))
{
if (node->children[i]->nShpCount == 0) //如果之前没有节点
{
node->children[i]->nShpCount += 1;
node->pShapeObj = 
(SHPMBRInfo*)malloc(sizeof(SHPMBRInfo)*node->children[i]->nShpCount);
}
else if (node->children[i]->nShpCount > 0)
{
node->children[i]->nShpCount += 1;
node->children[i]->pShapeObj = 
(SHPMBRInfo *)realloc(node->children[i]->pShapeObj,
sizeof(SHPMBRInfo)*node->children[i]->nShpCount);
}

pShpInfo.Box = itemRect;
pShpInfo.nID = key;
memcpy(node->children[i]->pShapeObj,
&pShpInfo,sizeof(SHPMBRInfo));
}
}
}

//当前节点没有空间对象
else if (0 == node->nShpCount)
{
node->nShpCount += 1;
node->pShapeObj = 
(SHPMBRInfo*)malloc(sizeof(SHPMBRInfo)*node->nShpCount);

pShpInfo.Box = itemRect;
pShpInfo.nID = key;
memcpy(node->pShapeObj,&pShpInfo,sizeof(SHPMBRInfo));
}
}

void InsertQuad(long key,MapRect &itemRect,QuadNode* pNode)
{
assert(pNode != NULL);

if (!IsQuadLeaf(pNode))    //非叶子节点
{
int nCorver = 0; //跨越的子节点个数
int iIndex = -1; //被哪个子节点完全包含的索引号
for (int i = 0; i < 4; i ++)
{
if (pNode->children[i]->Box.Contains(itemRect)
&& pNode->Box.Contains(itemRect))
{
nCorver += 1;
iIndex = i;
}
}

//如果被某一个子节点包含，则进入该子节点
if (/*pNode->Box.Contains(itemRect) || 
pNode->Box.Intersects(itemRect)*/1 <= nCorver)
{ 
InsertQuad(key,itemRect,pNode->children[iIndex]);
}

//如果跨越了多个子节点，直接放在这个节点中
else if (nCorver == 0)
{
if (pNode->nShpCount == 0) //如果之前没有节点
{
pNode->nShpCount += 1;
pNode->pShapeObj = 
(SHPMBRInfo*)malloc(sizeof(SHPMBRInfo)*pNode->nShpCount);
}
else
{
pNode->nShpCount += 1;
pNode->pShapeObj = 
(SHPMBRInfo *)realloc(pNode->pShapeObj,sizeof(SHPMBRInfo)*pNode->nShpCount);
}

SHPMBRInfo pShpInfo;
pShpInfo.Box = itemRect;
pShpInfo.nID = key;
memcpy(pNode->pShapeObj+pNode->nShpCount-1,&pShpInfo,sizeof(SHPMBRInfo));
}
}


//如果是叶子节点，直接放进去
else if (IsQuadLeaf(pNode))
{
if (pNode->nShpCount == 0) //如果之前没有节点
{
pNode->nShpCount += 1;
pNode->pShapeObj = 
(SHPMBRInfo*)malloc(sizeof(SHPMBRInfo)*pNode->nShpCount);
}
else
{
pNode->nShpCount += 1;
pNode->pShapeObj = 
(SHPMBRInfo *)realloc(pNode->pShapeObj,sizeof(SHPMBRInfo)*pNode->nShpCount);
}


SHPMBRInfo pShpInfo;
pShpInfo.Box = itemRect;
pShpInfo.nID = key;
memcpy(pNode->pShapeObj+pNode->nShpCount-1,&pShpInfo,sizeof(SHPMBRInfo));
}
}


void InsertQuad2(long key,MapRect &itemRect,QuadNode* pNode)
{
QuadNode *node = pNode; //保留根节点副本
SHPMBRInfo pShpInfo;


//节点有孩子
if (0 < node->nChildCount)
{
for (int i = 0; i < 4; i ++)
{  
//如果包含或相交，则将节点插入到此节点
if (node->children[i]->Box.Contains(itemRect)
|| node->children[i]->Box.Intersects(itemRect))
{
//node = node->children[i];
Insert(key,itemRect,node->children[i]);
}
}
}


//如果当前节点存在一个子节点时
else if (0 == node->nChildCount)
{
MapRect boxs[4];
node->Box.Split(boxs,boxs+1,boxs+2,boxs+3);


int cnt = -1;
for (int i = 0; i < 4; i ++)
{  
//如果包含或相交，则将节点插入到此节点
if (boxs[i].Contains(itemRect))
{
cnt = i;
}
}


//如果有一个矩形包含此对象，则创建四个孩子节点
if (cnt > -1)
{
for (int i = 0; i < 4; i ++)
{
//创建四个节点并插入相应的MBR
node->children[i] = InitQuadNode();
node->children[i]->Box = boxs[i];
}
node->nChildCount = 4;
InsertQuad2(key,itemRect,node->children[cnt]); //递归
}


//如果都不包含，则直接将对象插入此节点
if (cnt == -1)
{
if (node->nShpCount == 0) //如果之前没有节点
{
node->nShpCount += 1;
node->pShapeObj = 
(SHPMBRInfo*)malloc(sizeof(SHPMBRInfo)*node->nShpCount);
}
else if (node->nShpCount > 0)
{
node->nShpCount += 1;
node->pShapeObj = 
(SHPMBRInfo *)realloc(node->pShapeObj,
sizeof(SHPMBRInfo)*node->nShpCount);
}


pShpInfo.Box = itemRect;
pShpInfo.nID = key;
memcpy(node->pShapeObj,
&pShpInfo,sizeof(SHPMBRInfo));
}
}


//当前节点没有空间对象
/*else if (0 == node->nShpCount)
{
node->nShpCount += 1;
node->pShapeObj = 
(SHPMBRInfo*)malloc(sizeof(SHPMBRInfo)*node->nShpCount);


pShpInfo.Box = itemRect;
pShpInfo.nID = key;
memcpy(node->pShapeObj,&pShpInfo,sizeof(SHPMBRInfo));
}*/
}


bool IsQuadLeaf(QuadNode* node)
{
if (NULL == node)
{
return 1;
}
for (int i = 0; i < 4; i ++)
{
if (node->children[i] != NULL)
{
return 0;
}
}


return 1;
}


bool DelFalseNode(QuadNode* node)
{
//如果没有子节点且没有要素
if (node->nChildCount ==0 && node->nShpCount == 0)
{
ReleaseQuadTree(&node);
}


//如果有子节点
else if (node->nChildCount > 0)
{
for (int i = 0; i < 4; i ++)
{
DelFalseNode(node->children[i]);
}
}


return 1;
}


void TraversalQuadTree(QuadNode* quadTree,vector<int>& resVec)
{
QuadNode *node = quadTree;
int i = 0; 
if (NULL != node)
{
//将本节点中的空间对象存储数组中
for (i = 0; i < node->nShpCount; i ++)
{
resVec.push_back((node->pShapeObj+i)->nID);
}


//遍历孩子节点
for (i = 0; i < node->nChildCount; i ++)
{
if (node->children[i] != NULL)
{
TraversalQuadTree(node->children[i],resVec);
}
}
}


}


void TraversalQuadTree(QuadNode* quadTree,vector<QuadNode*>& arrNode)
{
deque<QuadNode*> nodeQueue;
if (quadTree != NULL)
{
nodeQueue.push_back(quadTree);
while (!nodeQueue.empty())
{
QuadNode* queueHead = nodeQueue.at(0); //取队列头结点
arrNode.push_back(queueHead);
nodeQueue.pop_front();
for (int i = 0; i < 4; i ++)
{
if (queueHead->children[i] != NULL)
{
nodeQueue.push_back(queueHead->children[i]);
}
}
}
}
}

void ReleaseQuadTree(QuadNode** quadTree)
{
int i = 0;
QuadNode* node = *quadTree;
if (NULL == node)
{
return;
}
else
{
for (i = 0; i < 4; i ++)
{ 
ReleaseQuadTree(&node->children[i]);
}
free(node);
node = NULL;
}
node = NULL;
}

long CalByteQuadTree(QuadNode* quadTree,long& nSize)
{
if (quadTree != NULL)
{
nSize += sizeof(QuadNode)+quadTree->nChildCount*sizeof(SHPMBRInfo);
for (int i = 0; i < 4; i ++)
{
if (quadTree->children[i] != NULL)
{
nSize += CalByteQuadTree(quadTree->children[i],nSize);
}
}
}
return 1;
}