Solution

考虑一条光线最终的作用效果只有两种：要么向下打入玻璃，要么向上打入玻璃。而我们要求的是向下打入第 $n$ 层玻璃的量。

所以对于每种作用方式建立一个未知数，或者也可以理解为一种广义的 DP：

设 $f_i$ 为向下打入第 $i$ 层玻璃的单位亮光
设 $g_i$ 为向上打入第 $i$ 层玻璃的单位亮光

如图，黑线是玻璃，黑线左边的数字是玻璃标号，蓝色线是第一种光线，红色光线是第二种光线。

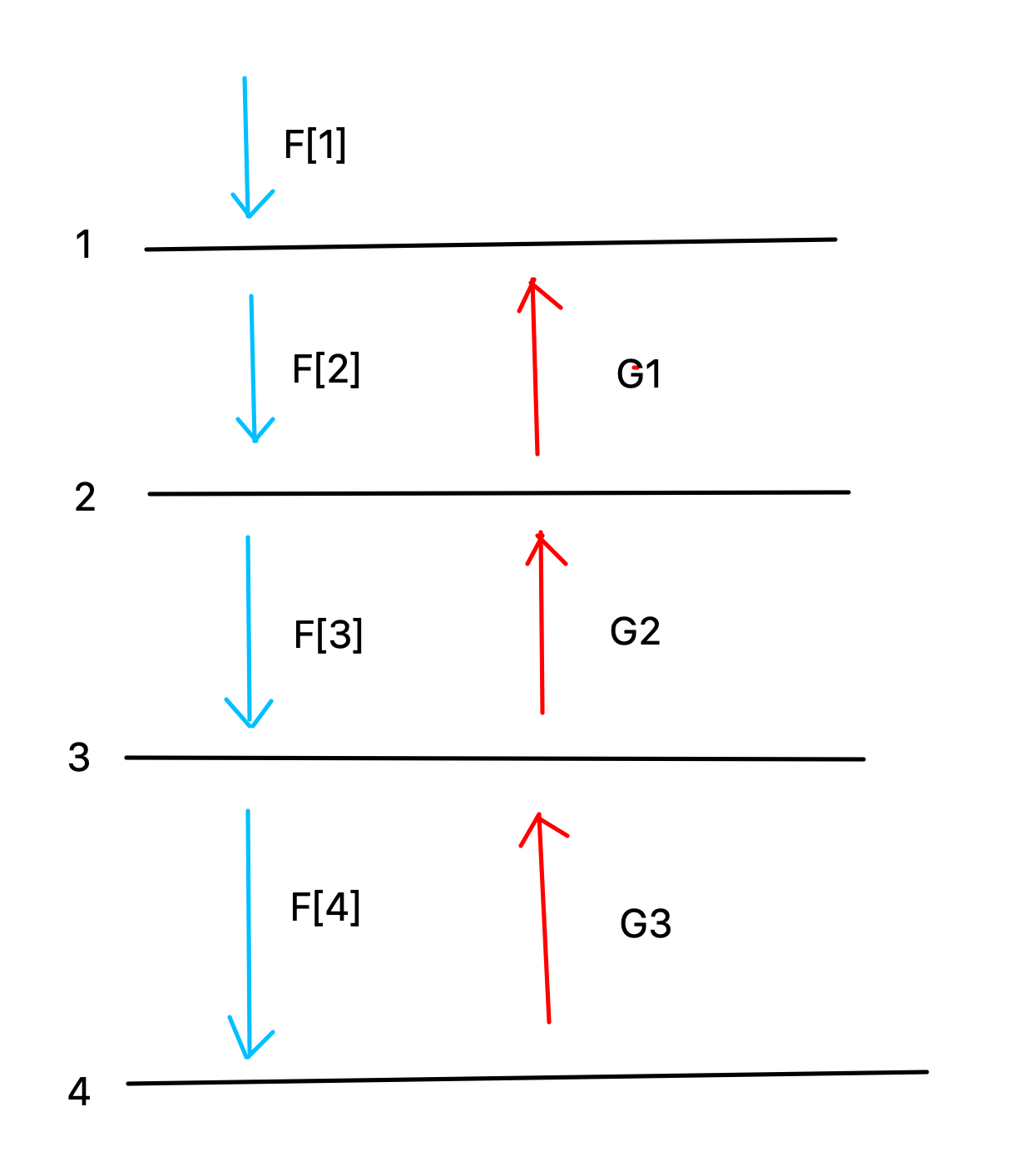
方程之间的等式

显然，考虑对于每一种作用光线由什么光线转化而成的即可，注意这里转化的方式是反射、投射：

$f_1 = 1$，为初始打入的光线。
$f_i\ (2 \le i \le n) = a_{i - 1} \% ·f_{i - 1} + b_{i - 1} \% \cdot g_{i - 1}$。（绿色箭头的转移方式）。
$g_n = 0$。
$g_{i}\ (1 \le i < n) = a_{i + 1}\% \cdot g_{i + 1} + b_{i + 1}\% \cdot f_{i + 1}$。（橙色箭头的转移方式）。

这样，我们就构建好了一个具有 $2n$ 个未知数，$2n$ 个方程的方程组。

发现如果知道 $f_{i}, g_{i}$，可以推出 $f_{i + 1}, g_{i + 1}$，因为 $f_1 = 0$，不妨设 $g_1 = x$。那么所有数都可以表示为 $ax + b$ 的形式。推至最后令 $g_n = 0$ 算出 $x$，最后带入 $x$ 算入相应的 $f_n$ 。

#include <iostream>
#include <cstdio>

using namespace std;

typedef long long LL;

const int N = 500005, P = 1e9 + 7;

int n, a[N], b[N], f[N][2], g[N][2];

int inline power(int a, int b) {
	int res = 1;
	while (b) {
		if (b & 1) res = (LL)res * a % P;
		a = (LL)a * a % P;
		b >>= 1;
	}
	return res;
}

int main() {
	scanf("%d", &n);
	int inv = power(100, P - 2);
	for (int i = 1; i <= n; i++) {
		scanf("%d%d", a + i, b + i);
		a[i] = (LL)a[i] * inv % P, b[i] = (LL)b[i] * inv % P;
	}
	f[1][0] = 1, g[1][1] = 1;
	for (int i = 2; i <= n; i++) {
		f[i][0] = ((LL)a[i - 1] * f[i - 1][0] + (LL)b[i - 1] * g[i - 1][0]) % P;
		f[i][1] = ((LL)a[i - 1] * f[i - 1][1] + (LL)b[i - 1] * g[i - 1][1]) % P;
		g[i][0] = (g[i - 1][0] - (LL)f[i][0] * b[i] % P + P) * power(a[i], P - 2) % P;
		g[i][1] = (g[i - 1][1] - (LL)f[i][1] * b[i] % P + P) * power(a[i], P - 2) % P;
	}
	int x = (LL)(P - g[n][0]) * power(g[n][1], P - 2) % P;
	printf("%lld\n", (f[n][0] + (LL)f[n][1] * x % P) * a[n] % P);
	return 0;
}

BJOI2019 光线

Solution

方程之间的等式

猜你喜欢