从零开始最优阵列处理（1）

从零开始

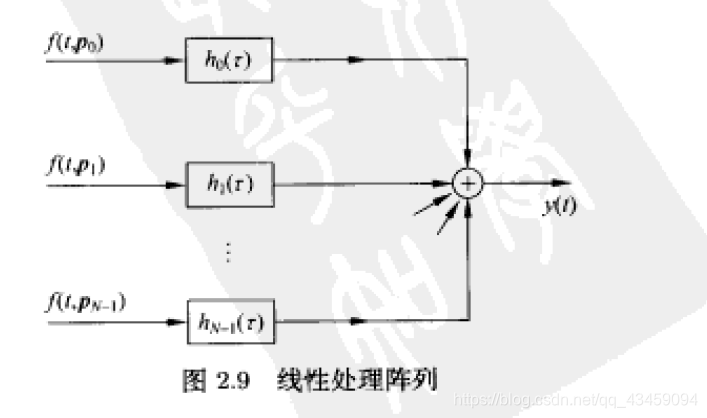
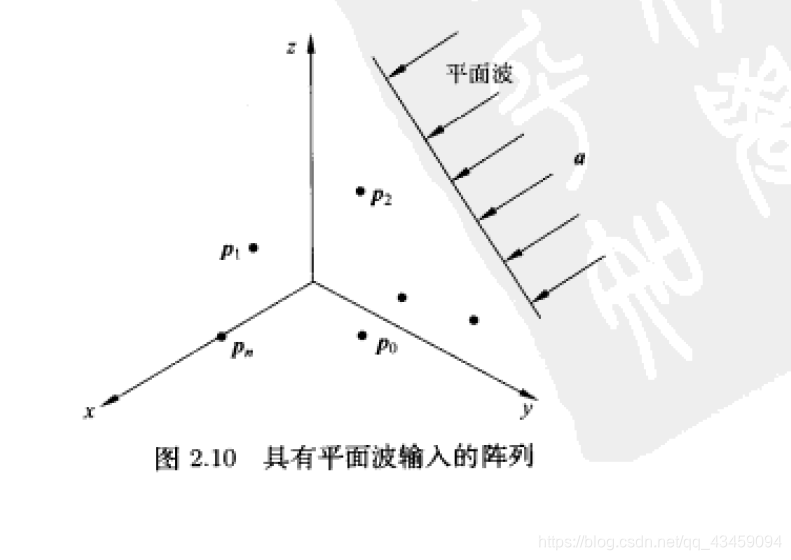
本人要开始做关于相控阵的毕设了。无奈基础太差，技术太菜，遂开始从零学起阵列处理方面的知识——以供复习和参考。
使用的教材是 H.L.Vans Trees ，Optimum Array Processing

啥是阵列处理

你想嘛，接收一个复杂的信号 拿着一根天线/麦克风在那杵着多捞啊。一个OV开头的摄像头模块都有很多感光阵元（这个。。其实和本文内容无关）。阵列处理中要经历加权处理（后文将提到） 所以理论上，阵列处理更能消除误差（或者更敏感，反正学着学着就知道了，不是吗）。

阵列流形矢量（Array Manifold Vector）

Now, 这里有个阵列，我们认为里面的每个阵元p都能接收到一个信号。简单来说，因为接收信号是在空间里采样，所以对信号的采样叫 空域采样（Spatial Sampling） 。
通过采样，我们可以得到一个矢量：
$\bm{f}(t,\bm{p})= \left[ \begin{matrix} f(t,\bm{p_0})\\ f(t,\bm{p_1})\\ .\\ .\\ .\\ f(t,\bm{p_{N-1}})\\ \end{matrix} \right]$
我们可以把这个矢量看成一个对于时间的一个函数表。对于这一坨数据。我们通常要用一个LTI滤波器处理：

卷积积分的形式：
$y(t)=\sum_{n=0}^{N-1}\int_{-\infty}^{\infty}h_n(t-\tau)f_n(\tau,\bm{p_n})d\tau$
简洁点，我们把 $h_n$变成一个向量：
$\bm{h}(\tau)= \left[ \begin{matrix} h_0(\tau)\\ h_1(\tau)\\ .\\ .\\ .\\ h_{N-1}(\tau)\\ \end{matrix} \right]$
我们又可以矢量表示 $y(t)$:
$y(t)=\int_{-\infty}^{\infty}\bm{h}^T(t-\tau)\bm{f}(\tau,\bm{p})d\tau$
让我们对 $y(t)$做傅里叶变换——时域卷积，频域乘积：
$\begin{aligned} Y(\omega)&=\int_{-\infty}^{\infty}y(t)e^{-j\omega t}dt\\ &=\bm{H^T}(\omega)\bm{F}(\omega) \end{aligned}$
到这 稍微有点迷糊，作为CTFT的前提条件——时间= $\infty$显然不可实现。其实我们这里有个前提：假设观察时间足够长以至于可以考虑为无限长。这样的话，我们就可以得到一个频域的向量了。
强调：频域向量内的每一个元素是各个阵元所收到的信号的频谱。
接下来，考虑一般情况，收到了一个平面波：

你看，收到的信号肯定有相位差吧！
我们令原点收到的信号为 $f(t)$：
$\bm{f}(t,\bm{p})= \left[ \begin{matrix} f(t-\tau_0)\\ f(t-\tau_1)\\ .\\ .\\ .\\ f(t-\tau_{N-1})\\ \end{matrix} \right]$
考虑如下的球形坐标系：

我们设这个平面波的传播方向为(在直角坐标系下）：
$\bm{a}= \left[ \begin{matrix} -\sin\theta cos\phi\\ -\sin\theta sin\phi\\ -cos\theta \end{matrix} \right]$
不用动脑子了，其相位差为：
$\tau_n=\frac{\bm{a^Tp_n}}{c}=-\frac{1}{c}[sin\theta cos\phi\bm{p_{x_n}}+sin\theta sin\phi\bm{p_{y_n}}+cos\theta\bm{p_{z_n}}]$
书上还有负方向的情况，简简单单定义 $\bm{u}=-\bm{a}$不赘述了。

咱们接着鼓捣式子：
讨论 $\omega\tau_n$, $\omega\tau_n=\frac{\omega}{c}\bm{a^Tp_n}$
在波 $cos(\omega t+\bm{k^Tx})$中， $\bm{k}=\frac{\omega}{c}\bm{a}$被称为波数（电磁场学过的，明明是个向量。。。）.
根据傅里叶时移频域变化情况，我们可以知道 $\bm{F}(\omega)$的第n个分量是： $e^{-j\omega\tau_n}F_{在零点的频谱！这句话以后都省略了！} (\omega)$
我们的讨论主题阵列流形矢量(AMV)就呼之欲出了。
$\bm{F}(\omega)=F(\omega)\bm{v_k(k)},\bm{v_k(k)}$就是AMV。
$\bm{v_k(k)}= \left[ \begin{matrix} e^{-j\bm{k^Tp_0}}\\ e^{-j\bm{k^Tp_1}}\\ .\\ .\\ .\\ e^{-j\bm{k^Tp_{N-1}}}\\ \end{matrix} \right]$

波束形成器（重构器）

课本上歪歪斜斜的写着‘波束形成器（beamformer)’五个字。我横竖睡不着，仔细看了半夜，才从字缝里看出字来，满本都写着两个字是‘重构’！

哎哟，这几个函数怎么鼓捣不完了，
我们设一个阵元的基函数（gay basis function）也就是每个阵元接收到的波为：
$f_n(t,\bm p_n)=e^{j(\omega t-\bm{k^Tp}_n)}$
或整个阵列接收到的信号矢量
$\begin{aligned} \bm f(t,\bm p)&=e^{j\omega t}\bm{v_k(k)}\\ &= \left[ \begin{matrix} e^{j(\omega t-\bm{k^Tp}_0)}\\ e^{j(\omega t-\bm{k^Tp}_1)}\\ .\\ .\\ .\\ e^{j(\omega t-\bm{k^Tp}_{N-1})}\\ \end{matrix} \right] \end{aligned}$
看看上文我们提到的 $\bm{v_k^H(k_s)}$我们可以知道上面的阵列处理器对这个平面波的响应是：
$\bm h(\tau)= \left[ \begin{matrix} \frac{1}{N}\delta(\tau+\tau_0)\\ \frac{1}{N}\delta(\tau+\tau_1)\\ .\\ .\\ .\\ \frac{1}{N}\delta(\tau+\tau_{N-1})\\ \end{matrix} \right]$
而频（空）域我们可以写成更聪明的形式，我们一共轭，复指数的幂直接变了个符号。
$\bm{H^T}(\omega)=\frac{1}{N}\bm{v_k^H(k_s)}= \frac{1}{N} \left[ \begin{matrix} e^{j\bm{k^Tp_0}}\\ e^{j\bm{k^Tp_1}}\\ .\\ .\\ .\\ e^{j\bm{k^Tp_{N-1}}}\\ \end{matrix} \right]^T$
其中 $\bm{k_s}$是我们感兴趣的电磁波波数。
再傻瓜点：
$\bm{H}(\omega)=\frac{1}{N}\bm{v_k^*(k_s)}$

频率-波数响应函数（Frequency-wavenumber response function）

别忘了，阵列处理是为了得到更好的结果。也就是得到一个更好的结果。
通过分析上面的式子，我们可以得到一个有趣的结论：
$y(t,\bm{k})=\bm H^T(\omega)\bm v_k(\bm k)e^{j\omega t}=e^{j\omega t}$
我们发现，一个频域矢量和一个时域的矢量相乘了，最后得到的是一个时域的响应。请记住，这不是特殊情况。我们可以做一个定义：
$\bm\gamma(\omega,\bm k)\triangleq\bm H^T(\omega)\bm v_k(\bm k)$
我们把它称为频率-波数响应函数（Frequency-wavenumber response function）。课本上的介绍如下（中文不好复制，遂复读英文版）：
The frequency-wavenumber response function describes the response to an arbitrary plane wave. In most physical applications there is a coupling bet,ween the temporal frequency $\omega$ and the spatial wavenumber $\bm k$ through the wave equation governing the propagation of the plane wave. Sometimes this can be a very simple relationship such as a plane wave in a homogeneous (and infinite) space; in other instances it can be quite complicated, such as the modal behavior in layered media that often occurs in underwater acoustics（水下声纳） and seismology（地震学）.