0.引言
对于树上问题,有许多特殊的求解方法,如:树链剖分。点分治算法也是其中之一,常用于解决树上路径问题。
1.0.问题的引入
给定一棵树,求这棵树的直径(树上最长链长度,n<=10^5)
解法1.两遍dfs:先任选一个起点t,通过dfs遍历整个树,找到最长路的终点v,再从v进行dfs,第二次dfs找到节点u,树的直径即为u->v的路径长度。(此非本文内容,证明不再撰述。)
解法2.暴力点分治
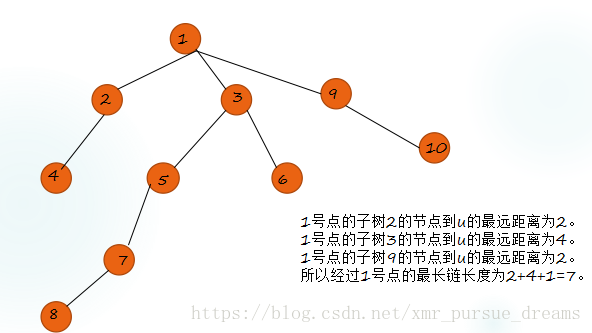
首先考虑枚举算法,对于一个节点u,我们可以先枚举所有经过u的链的长度s。
对于一个u的子树T,记f[T]=Max(dist(u,v)),v∈T。
显然,f[T]=max(f[A])+1(A是T的子树)。
则s=Max(f[T])+Max(f[ T' ])+1,T'≠T。
也就是说,s为子树中最远点v1与次远v2点的距离,且v1,v2不在同一个子树内,是即为经过u的最大链长度。
于是,我们可以求出u的每个子树的最远点距离,将最大和次大距离相加即是s。
此时,发现答案中与u有关的部分都求解完毕,只需要分治求解u的子树的s,最后合并答案即可。
这暴力枚举算法的时间复杂度是多少呢?
显然,这个算法的时间复杂度为O(sigma(size))的,也就是所有节点的子树大小之和。
发现这个算法在 数据退化为一条练的情况下,时间复杂度为O(n^2)。
如何优化???
我们需要尽量保持树的平衡,那么我们当然选择将子树的“重心”作为子树的根。
(重心:找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心)
我们发现选取重心之后,分治树节点u的每个子树大小一定小于u树的大小的一半。
于是时间复杂度为O(n log n),且有时根本达不到n log n的时间。
(
一般有两种合并方式:
1.子树依次合并,统计答案。
2.求出所有链的答案,再减去不包含这个节点的答案。
)
完美!!
1.1.点分治的实现
void get_center(int u,int father,int Size) //Size表示整棵树的大小
{
tree[u]={1,0}; //u节点初始化
for (int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if (size[v]||v==father) continue;
get_center(v,u,Size); //dfs
tree[u].size+=tree[v].size; //更新u子树大小
tree[u].heavy_son=get_max(tree[u].heavy_son,tree[v].size); //更新u的子树的最大值
}
tree[u].heavy_son=get_max(tree[u].heavy_son,Size-tree[u].size);
if (tree[u].heavy_son<MIN) {root=u,MIN=tree[u].heavy_son};
}
void divide(int u)
{
ans+=solve(u,0),visit[u]=1; //求所有链的答案
for (int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if (visit[v]) continue;
ans-=solve(v,e[i].d); //减去不经过u的答案
Smer=size[v];root=0;
MIN=INF; get_center(v,0);
divide(v);
}
}