理解ガウス分布：ガウス分布--Part1とユニティ

オリジナルリンク：  https://www.alanzucconi.com/2015/09/09/understanding-the-gaussian-distribution/

---

• 入門

平面上のランダムな点を生成する方法を考えてみましょう。これらの点は、敵、木、または任意のインスタンスを表すことができます。ユニティでは、最も簡単な方法は次のとおりです。

Vector3 position = new Vector3();
position.x = Random.Range(min,max),
position.y = Random.Range(min,max);
transform.position = position;

Random.Range図青いボックス内の点で発生することができます。これらの点は、均一ように表面全体の同じ点の密度こと、面内に分散されています。

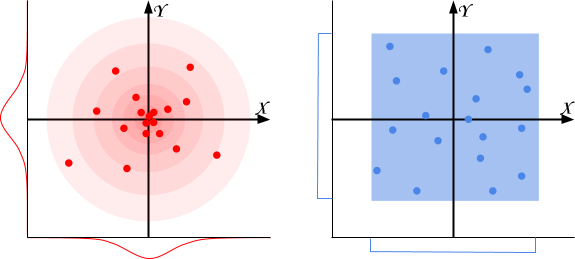
ガウス分布：だけ多くの自然現象の一つが均一に分布していない、彼らはより多くのそのオベイ地図上に赤いドットの左側にある別の確率分布のようなものです。親指のルールは次のとおりです。特定の値の周りに浮かんで自然なシーン値がある場合、それは可能性がガウス分布です。例えば：

傷害：敵、または武器の出力が発生する可能性があります。

粒子密度：数（火花、ほこりなど）オブジェクト近く特定の粒子。

緑の草や木：木や草の生態系の分布では、このような植物の湖の上の場所、または石の山の分布など。

 

• 一様分布を理解します

あなたがサイコロを転がしたとき、6:00 1/6の確率を投げます。確率の観点から左側に示すようにダイスは、サンプリング処理の離散値の一様分布からスローされます。均一な分布を有するそれぞれは、n側金型で表すことができます。1 / N：各平面内で選択される確率は同じxを有します。同様のRandom.Rangeの右側に示すように、関数戻り、均一範囲にわたって分布し、連続しています。

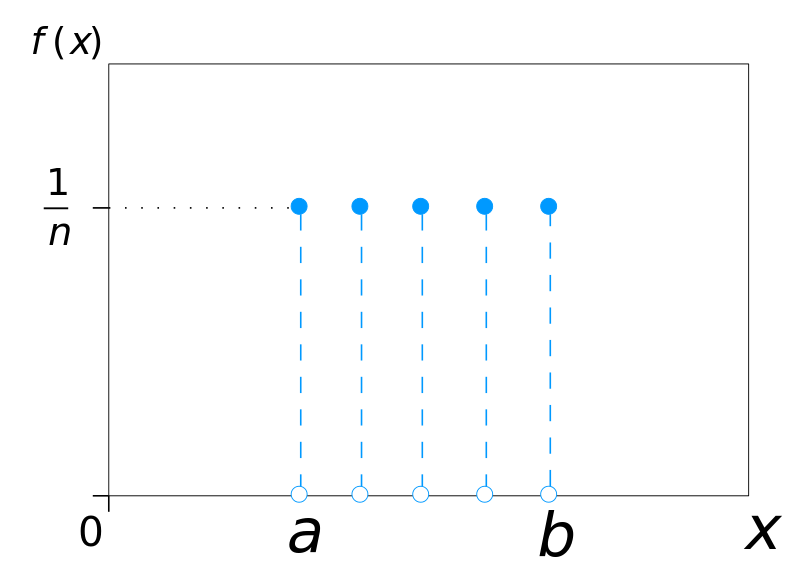
多くの場合、均一な分布が良い選択です。例えば、ランダムモデルのデッキから一枚のカードを選択すると、完全にそれを使用することができます。

 

• ガウス分布とは何ですか

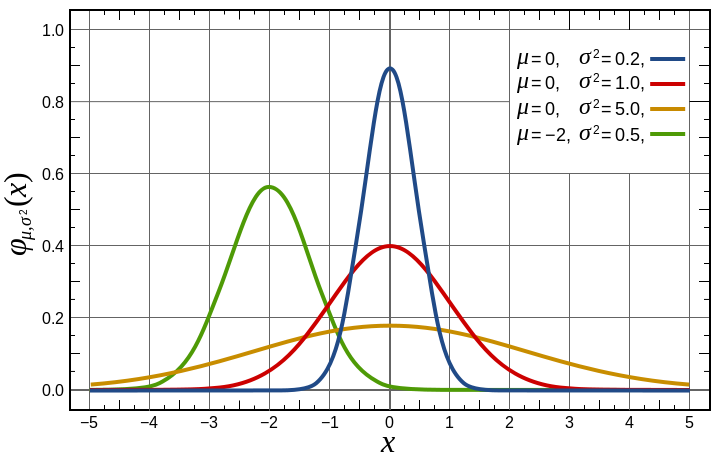
均一に分布されていない自然の中で多くの現象があります。あなたが家アゼリーの高さを測定する場合たとえば、あなたは、いくつかの値の出現数が他の値よりも有意に高いことがわかります。ほとんどの人は非常に高いまたは非常に低い類似した高さは、それは非常にまれです。ランダムに人を選ぶ部屋は、彼の高さが非常に近い平均に可能性があります。これらの現象は、典型的なガウス（または通常）分布です。与えられた値の発生確率にガウス分布です。

均匀分布仅有一个参数n，而高斯分布则有两个参数和 ，分别代表均值和方差。均值反映了概率曲线的中心位置所在，而方差则显示了某个服从该分布的随机值偏离均值的可能性。

若某个变量X服从高斯分布，则可将其写作：

 

• 高斯分布示例

让人吃惊的是，高斯分布可以通过正态分布产生。尽管两者在表达式上大相径庭，却有着密切的联系。我们想象一下，有个酒鬼正在下图中走路：他从图的左侧中间点出发，每次往右走一步时，他以等概率往上/下走一步。在x步以后他最有可能走到哪儿去呢？

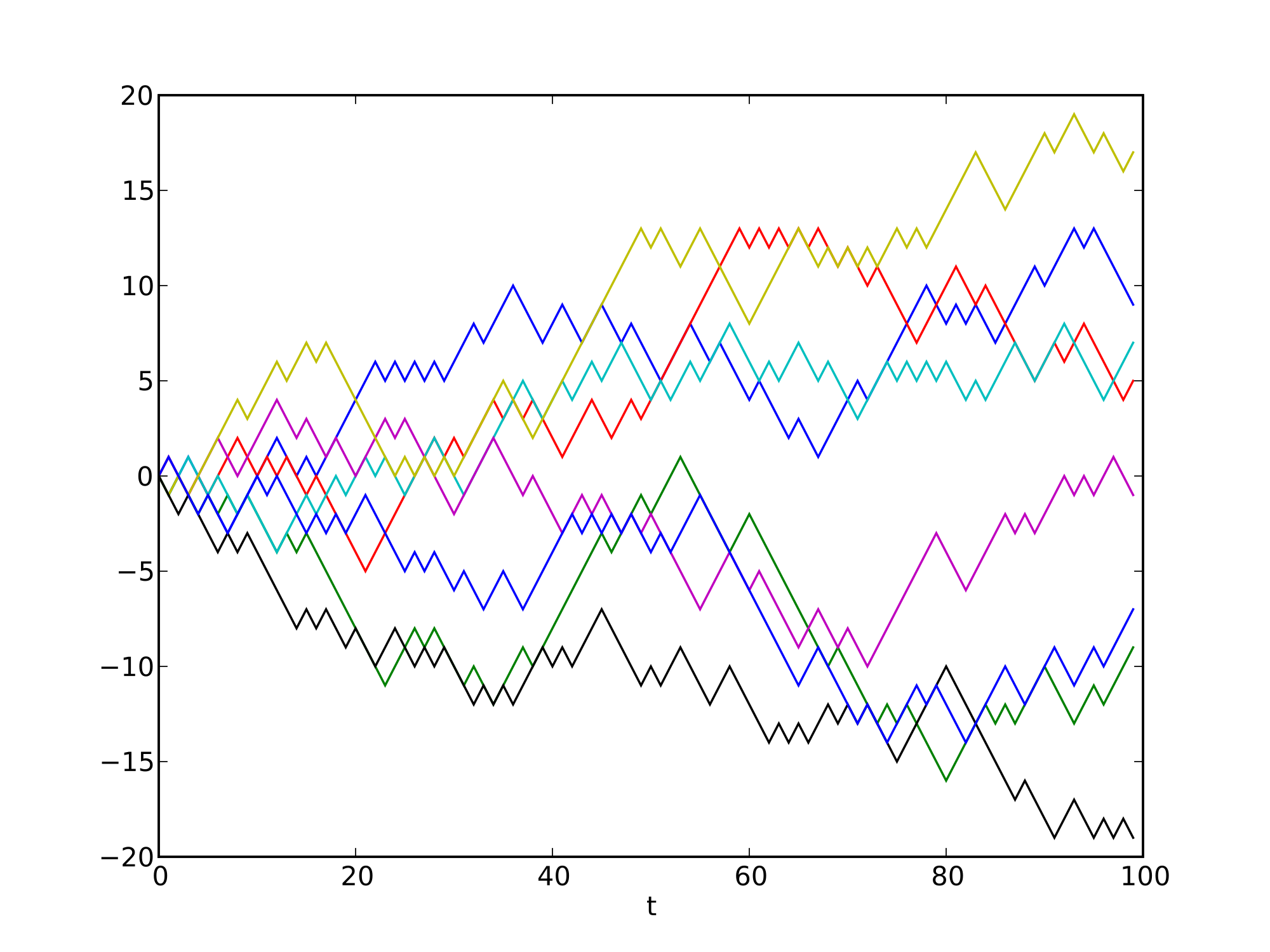
因为每步都是等概率的，所以上图所有的路径都是等概率发生的。然而越往两边的终点走，路线越少；越往中间走，路线越多。因此这个酒鬼最有可能待在离中心的终点附近。如果有足够多的酒鬼和足够的时间去走路，那么他们最终的位置计数图将很接近于高斯分布。

这个理论在19世纪被Francis Galton以bean machine实验验证过，如下图所示。这一实验背后隐藏着中心极限定理的思想：在自然界与生产中，一些现象受到许多相互独立的随机因素的影响，如果每个因素所产生的影响都很微小时，总的影响可以看作是服从正态分布的。

• 高斯分布推演

回头看看那个bean machine，想想每个球落入一个确定柱子里的概率是多少呢？

这就是所谓的二项分布。只是这个式子看上去一点也不“高斯分布”，怎么办呢？

令n趋近于无穷大，将离散的数值转为连续的——

首先，要将二项式系数扩展一下。这个式子由阶乘构成，而根据斯特林公式：，该式可转换成：，其中，。