記事の引用
https://mp.weixin.qq.com/s/5VIpNWci9YLY3m4gcYd6-w
https://blog.csdn.net/jason_sssss/article/details/118933988あ>
まとめ
フーリエ変換の核心は、「任意の連続周期信号は適切な正弦波の集合で構成できる」という点に基づいて、信号中の特定の周波数の正弦波を分解または再構成し、周波数に基づいて波形を解析します。 。
1. フーリエ変換の意味
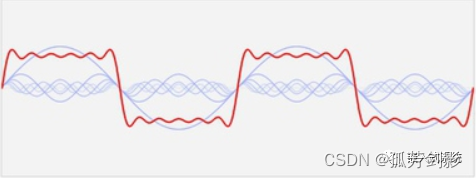
ほぼ周期的な方形波 (赤) は、フーリエの基礎となる 6 グループの正弦波 (青) を使用して合成できます。
デジタル信号処理または工学数学の基礎があれば、フーリエ変換の価値を理解できるでしょう。一般に、時間とともに変化する信号または波形は時間領域信号と呼ばれ、時間領域は数学関数または物理信号と時間との関係を表します。信号を周波数と振幅で表すことを周波数領域といいます。周波数領域は、信号の周波数特性を記述するために使用される座標系です。その数学的理論は当面無視され、組み込みシステム開発におけるその物理的意味または応用シナリオのみが議論されます。
時間領域と周波数領域は信号の基本的な特性です。時間領域の表現はより鮮明で直観的で、一般的な認識とより一致しますが、周波数領域の分析はより簡潔で、問題の分析はより深く、より深くなります。便利。
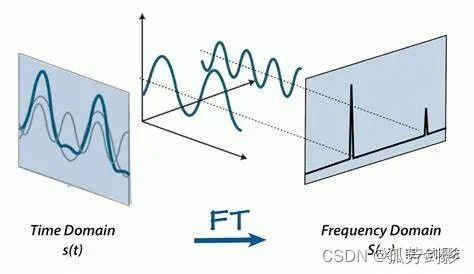
たとえば、下図の左側の時間領域信号は 2 つの正弦波の重ね合わせ効果に分解でき、右側の周波数領域信号は 2 つの正弦波の周波数と振幅を表します。波。フーリエ変換は、信号または波形のセグメントがどの正弦波で構成されているかを見つけることとして単純に理解できますが、複数の正弦波を逆に組み合わせた効果を導き出すためにも使用できます。
アニメーション形式に基づくと、パフォーマンスは次のとおりです。
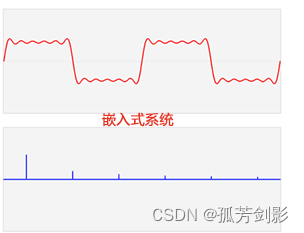
フーリエ変換は、信号解析手法であり、信号に関する詳細かつ定量的な研究を行うことができます。信号の構成と特性。スペクトルを通じて信号を正確かつ定量的に記述します。元の処理が難しい時間領域信号は、解析が容易な周波数領域信号に変換されます。つまり、フーリエ変換の核心は、時間領域から周波数領域への変換です。
2. 原則
デジタル信号は離散値であり、離散フーリエ変換 (DFT) に対応します。フーリエ変換は、時間領域と周波数領域の両方で離散形式をとります。時間領域信号のサンプリングを離散時間フーリエ変換に変換します。変換 (DTFT) 周波数領域サンプリング。形式的には、変換の両端のシーケンス (時間領域と周波数領域) は有限の長さですが、実際には、シーケンスの両方のセットが離散周期信号の主値シーケンスとして考慮される必要があります。有限長の離散信号に対して DFT を行った場合でも、周期拡張後の周期信号とみなして変換する必要があります。
実際のアプリケーションでは、高い計算効率を達成するために通常、高速フーリエ変換が使用されます 高速フーリエ変換 (高速フーリエ変換) は、離散フーリエ変換 (DFT) の高速アルゴリズムです。このアルゴリズムを使用すると、コンピュータが離散フーリエ変換を計算するために必要な乗算の数を大幅に削減でき、特に、変換されるサンプリング点 N が増えるほど、FFT アルゴリズムの計算量が大幅に節約されます。同様に、周波数領域から時間領域への変換を逆変換、逆高速フーリエ変換IFFT、逆離散フーリエ変換IDFTと呼びます。
(1) 高速フーリエ変換(FFT)の最適化原理







(2)base-2FFTアルゴリズムの導出




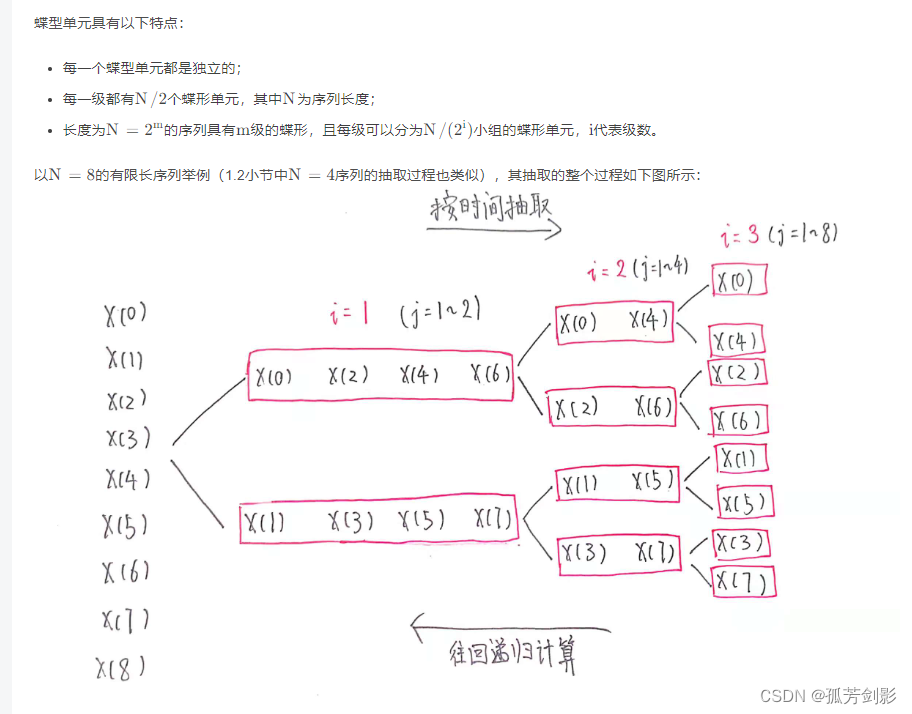
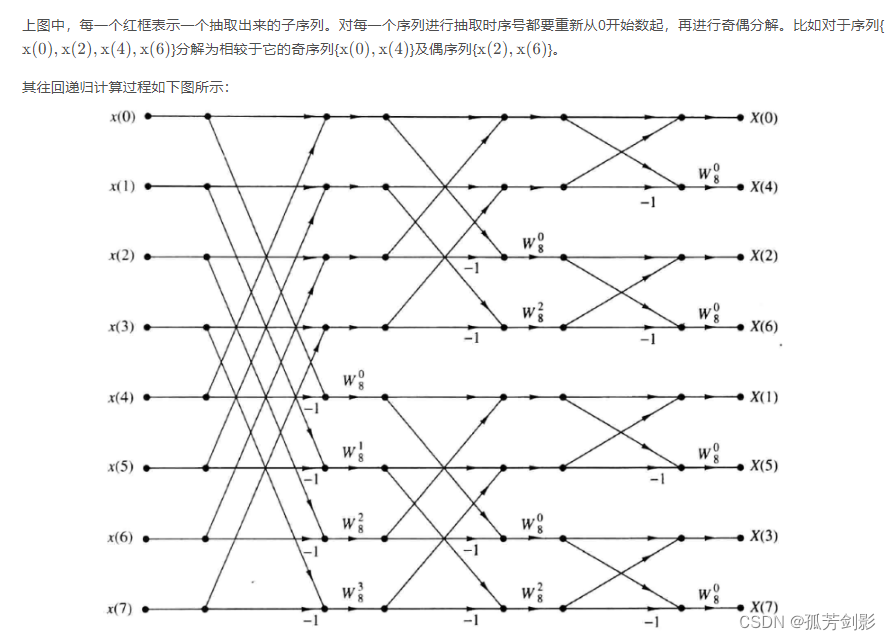
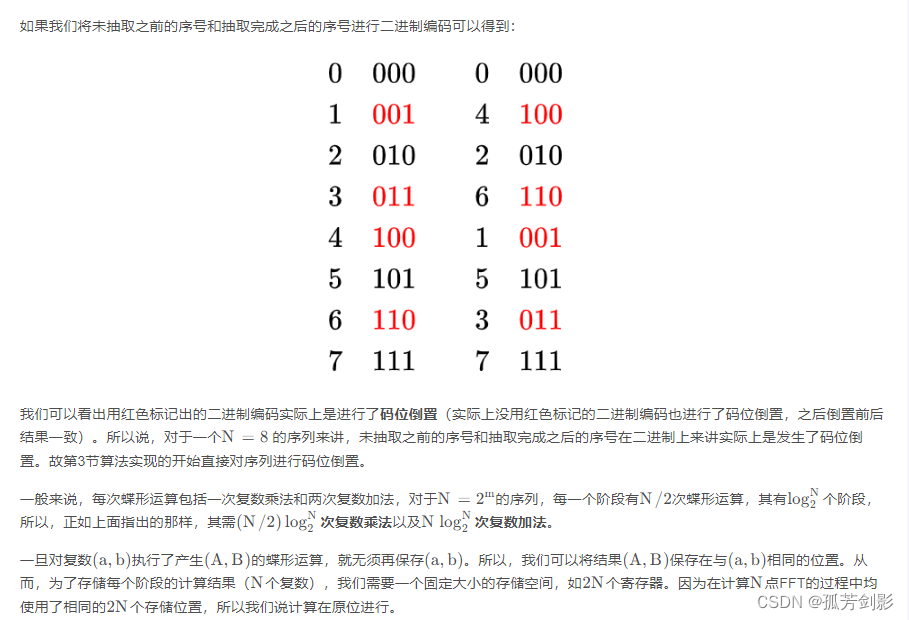
(3) Base-2FFT アルゴリズムの実装
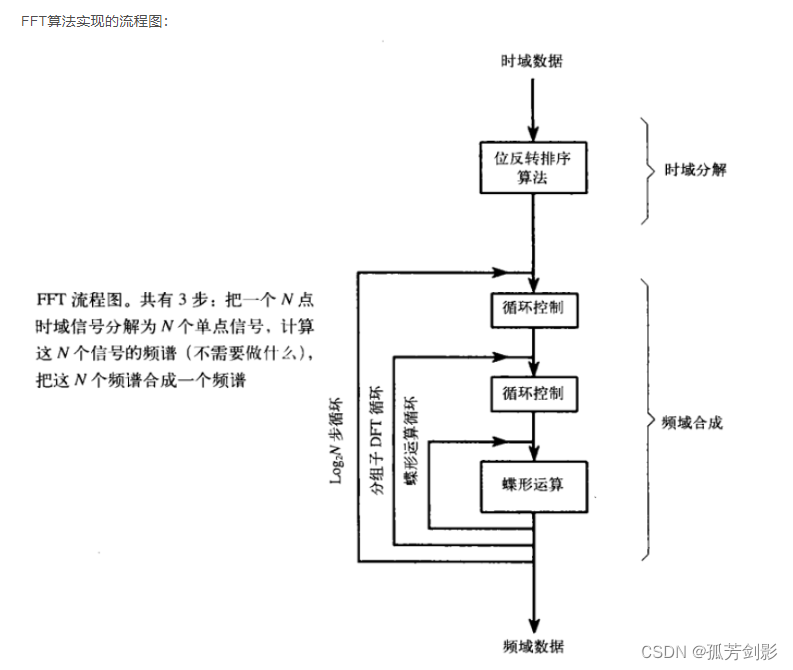
3. アプリケーション
一般に、高速フーリエ変換は、組み込みシステムで特定の信号セグメント内の混合クラッター干渉を分析したり、特定の周波数帯域を除去して逆変換したりするために使用されます。一部のハイエンド オシロスコープは、信号に対して高速フーリエ変換 (FFT) を実行し、高周波クラッタの周波数またはより大きな振幅の干渉源の周波数を直接表示できるため、回路の干渉を的を絞った方法でチェックできます。この記事では、主に fft/ifft を使用して干渉信号をフィルタリングする方法について説明します。
(1) Pythonをベースにデータソースを生成
1、python生成正弦波,以及混合波形,提取数值作为c语言FFT/IFFT的数据源
2、先进行FFT,输出幅频数据,导入Excel看看效果
3、对数据进行简单过滤
4、过滤后的数据进行IFFT运算,再导入Excel看还原的效果
# This is a Python script.
import numpy as np
import matplotlib.pyplot as plt
def sin_wave(A, f, fs, phi, t):
"""
:params A: 振幅
:params f: 信号频率
:params fs: 采样频率
:params phi: 相位
:params t: 时间长度
# 若时间序列长度为 t=1s,
# 采样频率 fs=1000 Hz, 则采样时间间隔 Ts=1/fs=0.001s
# 采样点个数为 n=t/Ts=1/0.001=1000, 即有1000个点,每个点间隔为 Ts
"""
Ts = 1/fs
n = t / Ts
n = np.arange(n) #生成一个包含从0到n-1的整数的数组,表示时间序列的索引。
y = A*np.sin(2*np.pi*f*n*Ts + phi*(np.pi/180)) #将角度值phi转换为弧度值的
return y
fs = 360*40
my_sin1 = sin_wave(100, 100, fs=fs, phi=0, t=0.08)
my_sin2 = sin_wave(20, 500, fs=fs, phi=0, t=0.08)
my_sin3 = sin_wave(10, 1100, fs=fs, phi=0, t=0.08)
x = np.arange(0, 0.08, 1/fs)
plt.xlabel('x-t (samRate=14400)')
plt.ylabel('y-A')
plt.grid() #用于在绘图时添加网格线
plt.plot(x, my_sin1, 'k--',label="f=100")
plt.plot(x, my_sin2, 'b--',label="f=500")
plt.plot(x, my_sin3, 'g--',label="f=1100")
plt.plot(x, my_sin1+my_sin2+my_sin3, 'r',label="mix")
plt.legend() #用于在图表中添加图例
plt.show()
np.savetxt("sin.txt",my_sin1+my_sin2+my_sin3, fmt='%.06f') #用于将数组数据保存到文本文件
def print_name(name):
print(f'Hi, {
name}')
if __name__ == '__main__':
print_name('fft test')
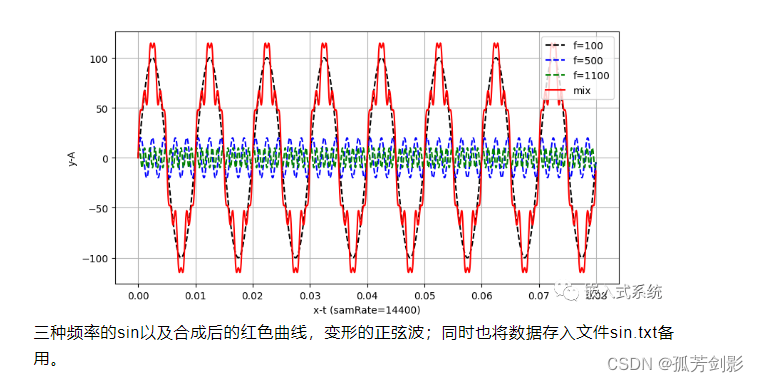
生成された波形は次のとおりです。