1. 関数、関数のフーリエ級数展開、フーリエ級数と関数の関係
1.1 フーリエ級数の係数式の導出
まずはフーリエ級数の係数式を導き出してみましょう. 実際、著者はすでに関連するメモを書いています. 詳細については、「なぜ関数を三角関数に分解する必要があるのか? (フーリエ級数)」を参照してください。



f ( x ) 〜 a 0 2 + ∑ n = 1 ∞ ( an cos n π xl + bn sin n π xl ) ( x ∈ R ) f ( x ) = a 0 2 + ∑ n = 1 ∞ ( an cos n π xl + bn sin n π xl ) ( − l < x < l ) a 0 = 1 l ∫ − llf ( x ) dx = 2 l ∫ 0 lf ( x ) dx an = 1 l ∫ − llf ( x ) cos n π xldx = 2 l ∫ 0 lf ( x ) cos n π xldx bn = 1 l ∫ − llf ( x ) sin n π xldx = 2 l ∫ 0 lf ( x ) sin n π xldxf(x)\sim \frac{a_0}{2}+\sum\limits_{n=1}^{\infty}(a_n\cos\frac{n\pi x}{l}+b_n\sin\frac {n\pi x}{l})(x\in \boldsymbol{R})\\ ~\\ f(x)= \frac{a_0}{2}+\sum\limits_{n=1}^{ \infty}(a_n\cos\frac{n\pi x}{l}+b_n\sin\frac{n\pi x}{l})(-l\lt x\lt l)\\ ~\\ a_0 =\frac{1}{l}\int_{-l}^{l}f(x)dx=\frac{2}{l}\int_{0}^{l}f(x)dx\\ ~ \\ a_n=\frac{1}{l}\int_{-l}^{l}f(x)\cos\frac{n\pi x}{l}dx=\frac{2}{l}\ int_{0}^{l}f(x)\cos\frac{n\pi x}{l}dx\\ ~\\b_n=\frac{1}{l}\int_{-l}^{l}f(x)\sin\frac{n\pi x}{l}dx=\frac{2}{l}\int_{ 0}^{l}f(x)\sin\frac{n\pi x}{l}dxf ( x )〜2ある0+n = 1∑∞( _んコス私nπx _+bん罪私nπx _) ( ×∈R ) f ( x )=2ある0+n = 1∑∞( _んコス私nπx _+bん罪私nπx _) ( − l<バツ<l ) ある0=私1∫− l私f ( x ) d x=私2∫0私f ( x ) d x あるん=私1∫− l私f ( x )コス私nπx _dx _=私2∫0私f ( x )コス私nπx _dx _ bん=私1∫− l私f ( x )罪私nπx _dx _=私2∫0私f ( x )罪私nπx _
上式のd xIf l = π l=\pi私=π
f ( x ) 〜 a 0 2 + ∑ n = 1 ∞ ( an cos nx + bn sin nx ) ( x ∈ R ) f ( x ) = a 0 2 + ∑ n = 1 ∞ ( an cos nx + bn sin nx ) ( − π < x < π ) a 0 = 1 π ∫ − π π f ( x ) dx = 2 π ∫ 0 π f ( x ) dx an = 1 π ∫ − π π f ( x ) cos nxdx = 2 π ∫ 0 π f ( x ) cos nxdx bn = 1 π ∫ − π π f ( x ) sin nxdx = 2 π ∫ 0 π f ( x ) sin nxdxf(x)\sim \frac{a_0}{2}+\sum\limits_{n=1}^{\infty}(a_n\cos nx+b_n\sin nx)(x\in \boldsymbol{R})\\ ~\\ f (x)= \frac{a_0}{2}+\sum\limits_{n=1}^{\infty}(a_n\cos nx+b_n\sin nx)(-\pi\lt x\lt \pi) \\ ~\\ a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx=\frac{2}{\pi}\int_{0}^{ \pi}f(x)dx\\ ~\\ a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nxdx=\frac{2}{ \pi}\int_{0}^{\pi}f(x)\cos nxdx\\ ~\\ b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f( x)\sin nxdx=\frac{2}{\pi}\int_{0}^{\pi}f(x)\sin nxdxf ( x )〜2ある0+n = 1∑∞( _んコスn ×+bん罪n x ) ( x∈R ) f ( x )=2ある0+n = 1∑∞( _んコスn ×+bん罪n x ) ( − π<バツ<p ) ある0=円周率1∫−p _pf ( x ) d x=円周率2∫0pf ( x ) d x あるん=円周率1∫−p _pf ( x )コスn × d ×=円周率2∫0pf ( x )コスn × d × bん=円周率1∫−p _pf ( x )罪n × d ×=円周率2∫0pf ( x )罪n × d ×
1.2 関数をフーリエ級数に拡張する
2008 年の数値 1
関数f ( x ) = 1 − x 2 ( 0 ≤ x ≤ π ) f(x)=1-x^2(0\leq x\leq \pi) を設定します。f ( x )=1−バツ2 (0≤バツ≤π )はコサインの形でフーリエ級数に展開され、その級数∑ n = 1 ∞ ( − 1 ) n − 1 n 2 \sum\limits_{n=1}^{\infty}\frac{(- 1)^{n-1}}{n^2}n = 1∑∞n2( − 1 )n − 1コサインの形でフーリエ級数に展開するため
、サイン級数は含まれず、bn = 0 b_n=0bん=0
f ( x ) 〜 a 0 2 + ∑ n = 1 ∞ an cos nx ( x ∈ R ) f ( x ) = a 0 2 + ∑ n = 1 ∞ an cos nx ( − π ≤ x ≤ π ) a 0 = 1 π ∫ − π π 1 − x 2 dx = 2 π ∫ 0 π 1 − x 2 dx = 2 ( 1 − π 2 3 ) an = 1 π ∫ − π π ( 1 − x 2 ) cos nxdx = 2 π ∫ 0 π ( 1 − x 2 ) cos nxdx = ( − 1 ) n + 1 ⋅ 4 n 2 f(x)\sim \frac{a_0}{2}+\sum\limits_{n= 1}^{\infty}a_n\cos nx(x\in \boldsymbol{R})\\ ~\\ f(x)= \frac{a_0}{2}+\sum\limits_{n=1}^ {\infty}a_n\cos nx(-\pi\leq x\leq \pi)\\ ~\\ a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}1- x^2dx=\frac{2}{\pi}\int_{0}^{\pi}1-x^2dx=2(1-\frac{\pi^2}{3})\\ ~\\ a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}(1-x^2)\cos nxdx=\frac{2}{\pi}\int_{0}^{ \pi}(1-x^2)\cos nxdx=\frac{(-1)^{n+1}\cdot4}{n^2}f ( x )〜2ある0+n = 1∑∞あるんコスn x ( x∈R ) f ( x )=2ある0+n = 1∑∞あるんコスn x ( − π≤バツ≤p ) ある0=円周率1∫−p _p1−バツ2dx __=円周率2∫0p1−バツ2dx __=2 ( 1−3円周率2) あるん=円周率1∫−p _p( 1−バツ2 )コスn × d ×=円周率2∫0p( 1−バツ2 )コスn × d ×=n2( − 1 )n + 1⋅4
f ( x ) = 1 − π 2 3 + ∑ n = 1 ∞ ( − 1 ) n + 1 ⋅ 4 n 2 cos nx ( − π ≤ x ≤ π ) f ( 0 ) = 1 − π 2 3 + ∑ n = 1 ∞ ( − 1 ) n + 1 n 2 ( − π ≤ x ≤ π ) f ( 0 ) = 1 − 0 2 = 1 1 = 1 − π 2 3 + 4 ∑ n = 1 ∞ ( − ) n + 1 n 2 ( − π ≤ x ≤ π ) ∑ n = 1 ∞ ( − 1 ) n + 1 n 2 = π 2 12 f(x)= 1-\frac{\pi^2}{3} +\ sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot4}{n^2}\cos nx(-\pi\leq x\leq \pi )\ \ ~\\ f(0)=1-\frac{\pi^2}{3}+4\sum\limits_{n=1}^{\infty}\frac{(-1)^{n +1 }}{n^2}(-\pi\leq x\leq \pi)\\ ~\\ f(0)=1-0^2=1\\ ~\\ 1=1-\frac{ \pi ^2}{3}+4\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}}{n^2}(-\pi\leq x \leq \pi)\\ ~\\ \sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}}{n^2}=\frac{\pi^ 2} {12}f ( x )=1−3円周率2+n = 1∑∞n2( − 1 )n + 1⋅4コスn x ( − π≤バツ≤p ) f ( 0 )=1−3円周率2+4n = 1∑∞n2( − 1 )n + 1( − p≤バツ≤p ) f ( 0 )=1−02=1 1=1−3円周率2+4n = 1∑∞n2( − 1 )n + 1( − p≤バツ≤p ) n = 1∑∞n2( − 1 )n + 1=12円周率2
1.3 関数間の関係の解析、関数のフーリエ級数展開、フーリエ級数と関数
グラフ化のプロセスは次のとおりです。

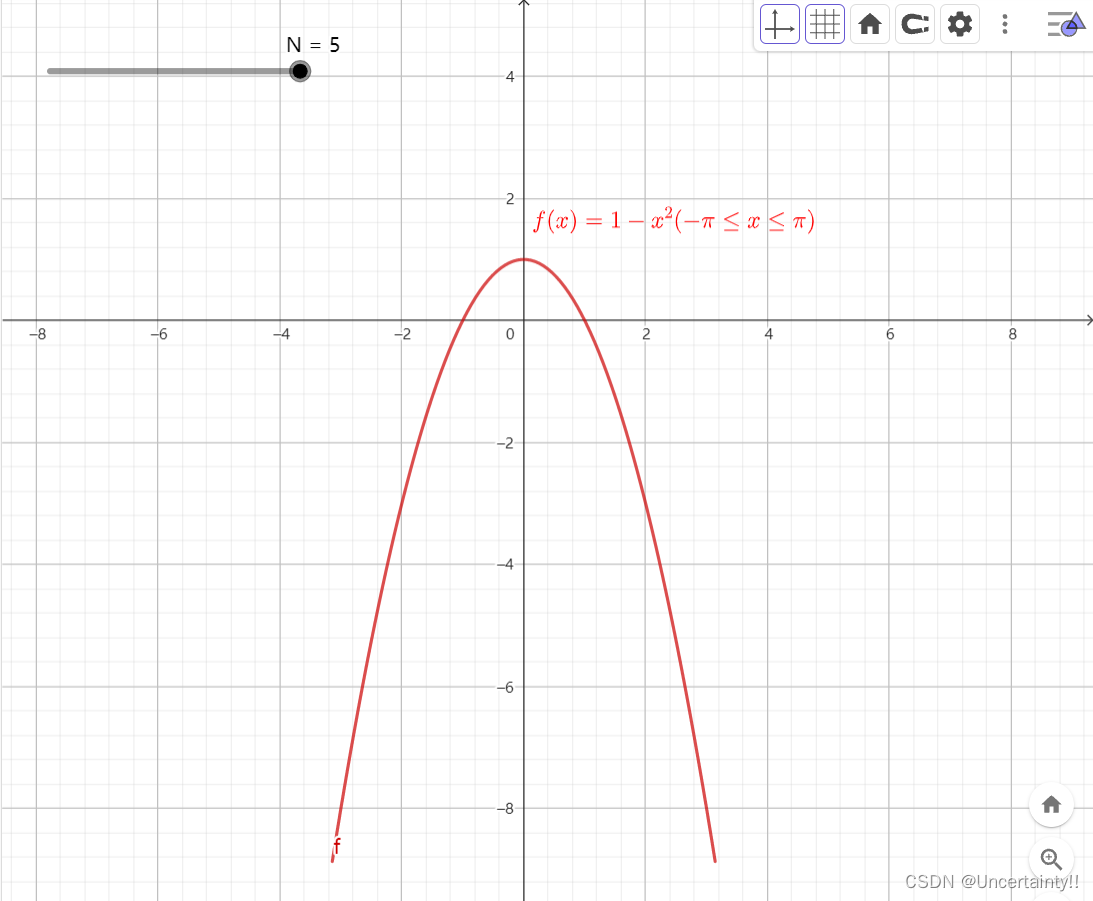
関数f ( x ) = 1 − x 2 ( 0 ≤ x ≤ π ) f(x)=1-x^2(0\leq x\leq \pi)f ( x )=1−バツ2 (0≤バツ≤π )

コサイン級数の部分コサイン波
an cos nx a_n\cos nxあるんコス
この写真のn x nnnは 1 ~ 5 のみで、合計 5 つの余弦波が得られます。

各余弦波 (緑) は重ね合わされて余弦級数 (オレンジ) を形成します
∑ n = 1 ∞ an cos nx \sum\limits_{n=1}^ {\infty }a_n\cos nxn = 1∑∞あるんコスn x

コサイン級数とa 0 / 2 a_0/2ある0/2 (青)の画像
a 0 2 + ∑ n = 1 ∞ an cos nx \frac{a_0}{2}+\sum\limits_{n=1}^{\infty}a_n\cos nx2ある0+n = 1∑∞あるんコスn ×

関数f ( x ) f(x)f ( x ) (赤) とそのフーリエ級数をコサイン形式に展開した画像 (青)

上図では、赤色が関数、青色が関数のフーリエ級数展開、関数と関数のフーリエ級数展開が重なっている部分が和関数、関数の重なっている部分が関数です。フーリエ級数の和関数である収束領域を超えると等しくなくなります
n が 1 ~ 30 の場合、フーリエ級数の和関数は基本的に関数と完全に一致します。!

描画プロセスの概要
 f(x)
f(x)
|
 a_ncos(nx)
a_ncos(nx)
|
 コサイン級数
コサイン級数
|
 関数と余弦級数
関数と余弦級数
|