1. 単一ソースの最短パス
重み付き有向グラフ G = (V,E) の場合、各エッジの重みは非負の実数になります。さらに、ソースと呼ばれる V の頂点も指定されます。今ソースから他のすべての頂点までの最短パス長を計算するには。ここでの道路の長さは、道路の両側の権利の合計を指します。この問題は、単一ソース最短パス問題と呼ばれることがよくあります。
1.1 アルゴリズムの基本的な考え方
ダイクストラのアルゴリズムは、単一ソースの最短経路問題を解決するための貪欲なアルゴリズムです。 ダイクストラのアルゴリズムの関連概念
: S [u]: S を基準とした s から u までの最短経路の長さ short [u]: からの最短経路の長さs から u までの 距離[u]>=short[u]
1.2 アルゴリズム設計のアイデア
入力: 有向グラフ G=(V,E)、V={1,2,…,n}、s=1
出力: s から各頂点への最短経路
1.初期 S={1}
2. i∈VS の場合
、S を基準にして 1 から i までの最短パスを計算します。長さ dist[i]、パスは ∞ または maxint 3として記録できません。VS で最小の dist 値を持つ j を選択し、j を S に追加し、の頂点を変更します。 VS dist 値
4. S=V になるまで上記のプロセスを継続します。
基本的な考え方は、頂点セット S を設定し、継続的に貪欲な選択を行ってこのセットを拡張します。頂点は、ソースから頂点までの最短パスの長さが既知である場合に限り、集合 S に属します。
最初は、S にはソースのみが含まれています。u が G の頂点であるとします。Sの頂点のみを通過するソースから u までのパスは、ソースから u までの特別なパスと呼ばれ、配列 dist を使用して、それぞれに対応する最短の特別なパスの長さを記録します。現在の頂点。ダイクストラのアルゴリズムは、毎回 VS から最短の特別なパス長を持つ頂点 u を取り出し、u を S に追加し、配列 dist に必要な変更を加えます。S に V のすべての頂点が含まれると、dist はソースから他のすべての頂点までの最短パスの長さを記録します。。
たとえば、右の図の有向グラフダイクストラのアルゴリズムを適用してソース頂点 1 から他の頂点までの最短パスを計算するプロセスを、次のページの表に示します。
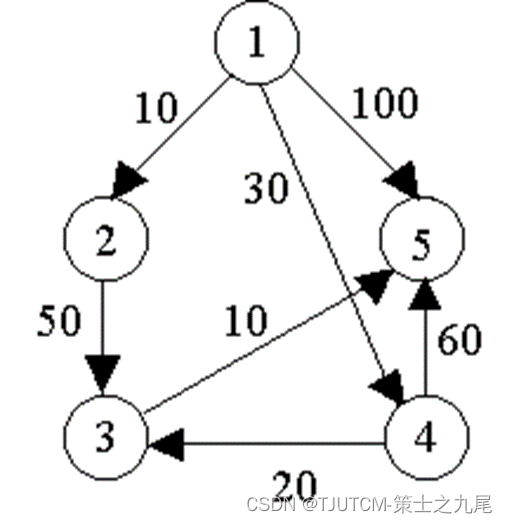
ダイクストラのアルゴリズムの反復プロセス:
1.3 アルゴリズムの正確さと計算の複雑さ
(1)貪欲な選択特性
(2)最適な部分構造特性
(3)計算の複雑さ
n 個の頂点と e 個のエッジを持つ重み付き有向グラフの場合、このグラフが重み付き隣接行列で表される場合、ダイクストラ アルゴリズムは次のようになります。メインループ本体時間がかかります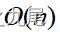
。このループは n-1 回実行する必要があるため、ループが完了するまでに時間がかかります
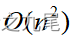。アルゴリズムの残りの部分には 5 分以上の時間はかかりません
。
1.4 帰納的証明のアイデア
命題: アルゴリズムが k 番目のステップに到達すると、S の各ノード i について、dist[i]=short[i]
帰納基底
k=1、S={s},dist[s]=short[s] =0
帰納ステップ
証明: 命題が k に対して真であると仮定すると、命題は k+1 に対しても真です
1.5 帰納法による証明
命題が k に対して真であると仮定し、頂点 v (エッジ <u,v>) を選択するための k+1 ステップ アルゴリズムを検討します。
別の sv パス L があり、S の最後の頂点が x で、Vs の最初の頂点 y を通過し、次に のパスを通って y から v に到達する場合、dist[v]=short[v] であることを証明する必要があります。VS
2. 最小スパニングツリー
G = (V, E) を無向接続加重グラフ、つまりネットワークとします。。E の各エッジ (v,w) の重みは c[v][w] です。G の部分グラフ G' が G のすべての頂点を含むツリーである場合、G' はGのスパニング ツリーと呼ばれます。スパニング ツリー上の各エッジの重みの合計は、スパニング ツリーのコストと呼ばれます。。G のすべてのスパニング ツリーの中で、コストが最も小さいスパニング ツリーを G の最小スパニング ツリーと呼びます。
ネットワークの最小スパニング ツリーは、実際に広く使用されています。たとえば、通信ネットワークを設計する場合、グラフの頂点を使用して都市を表し、エッジ (v, w) の重み c[v][w] を使用して都市 v 間の通信回線を確立するのに必要なコストを表します。および都市 w の場合、最小のスパニング ツリーは、通信ネットワークを確立するための最も経済的なソリューションを提供します。
2.1 最小スパニングツリープロパティ
貪欲なアルゴリズム設計戦略を使用すると、最小スパニング ツリーを構築するための効果的なアルゴリズムを設計できます。このセクションでは、最小スパニング ツリーを構築するためのPrim アルゴリズムとKruskal アルゴリズムを紹介します。は、貪欲なアルゴリズム設計戦略を適用した例とみなすことができます。。これら 2 つのアルゴリズムは異なる方法で貪欲な選択を行いますが、両方とも次の最小スパニング ツリー プロパティを利用します。G
= (V, E) を接続された重み付きグラフとし、U を V の適切なサブセットとします。(u,v)E、および uU、vVU、およびそのようなすべてのエッジの中で、(u,v) の重み c[u][v] が最小である場合、最小ツリーが存在する必要があります。エッジの 1 つとして (u, v) を持つ G スパニング ツリーの。このプロパティは、MST プロパティと呼ばれることもあります。
2.1.1 スパニングツリーのプロパティ
G が n 次の接続グラフであると仮定すると、
T にはサイクルがなく、 n-1 個のエッジがある場合に限り、 T は G のスパニング ツリーになります。
T が G の全域木であり、e が T に属さない場合、T∪{e} にはサイクル C (ループ) が含まれます。
円 C のエッジを削除すると、G の別のスパニング ツリー T' が得られます。
2.1.2 スパニングツリープロパティの適用
アルゴリズムのステップ: エッジの選択
制限：ループを形成しない
カットオフ条件:エッジの数が n-1 に達したときに
スパニング ツリー T を改善する方法
: 非ツリー エッジ e を T に追加してループ C を形成し、C からツリー エッジ ei を削除して新しいスパニング ツリー T' W(T
' )-W(T)=W(e)-W(ei)
W(e)<=W(ei) の場合、W(T')<=W(T)
2.2 プリムのアルゴリズム
G=(V,E) が接続された重み付けグラフ V={1,2,…,n} であると仮定します。
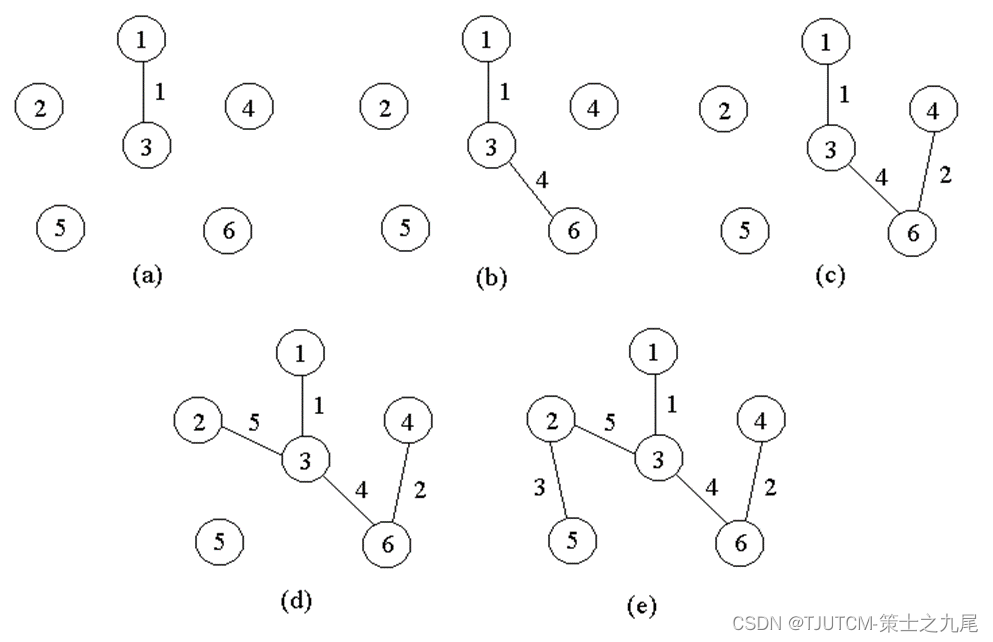
G の最小スパニング ツリーを構築するためのPrim のアルゴリズムの基本的な考え方は次のとおりです。まず S={1} を設定し、次に S が V の適切なサブセットである限り、次の貪欲な選択を行います。select iS , 条件を満たす jVS、そして c[i][j] が最小となる辺は頂点 j を S に追加します。このプロセスは S=V まで継続します。
このプロセスで選択されたすべてのエッジは、G の最小スパニング ツリーを正確に構成します。
最小スパニング ツリーのプロパティと数学的帰納法を使用すると、上記のアルゴリズムのエッジ セット T には常に G の特定の最小スパニング ツリー内のエッジが含まれることを証明するのは簡単です。。したがって、アルゴリズムの最後には、T のすべてのエッジが G の最小スパニング ツリーを形成します。
たとえば、右図の重み付きグラフについて、Prim のアルゴリズムに従ってエッジを選択するプロセスを次ページの図に示します。
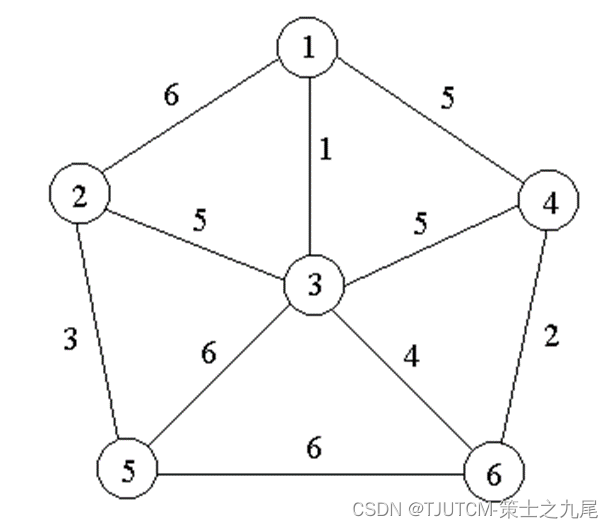
2.2.1 正しさの証明
命題：k<n の場合、アルゴリズムの最初の k ステップで選択されたエッジを含む最小スパニング ツリーが存在します。。
帰納基底: k=1、エッジ e={1,i} を含む最小スパニング ツリー T が存在します。ここで、{1,i} は 1 に関連付けられたすべてのエッジの中での最小の重みです。
帰納ステップ:アルゴリズムの最初の k ステップで選択されたエッジが最小全域ツリーのエッジを構成し、アルゴリズムの最初の k+1 ステップで選択されたエッジも最小全域ツリーのエッジを構成すると仮定します。
2.2.2 帰納的基底
証明: 関連するノード 1 の最小重みエッジ e={1,i} を含む
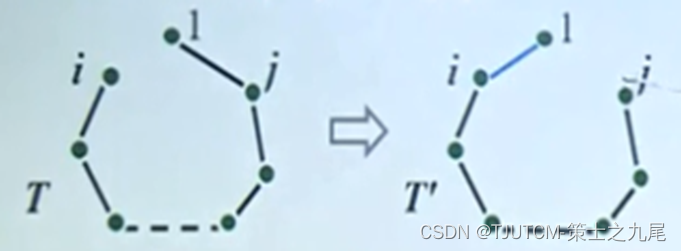
最小スパニング ツリー T が存在します。 証明: T が {1,i} を含まないと仮定して、T を最小スパニング ツリーとします。 T∪ {1,i} にはサイクルが含まれており、サイクルのもう一方のエッジ {1,j} は 1 に関連付けられています。{1,j} を {1,i} に置き換えてツリー T' を取得すると、T' もスパニング ツリーになり、W(T')<=W(T)
2.2.3 導入ステップ
アルゴリズムが k ステップ進み、スパニング ツリーのエッジが e1、e2、...ek で、これらのエッジの端点が集合 S を形成すると仮定します。これらのエッジを含む G の最小スパニング ツリー T が存在すると仮定します。
アルゴリズムのステップ k+1 で、頂点 ik+1 が選択されます。その後、ik+1 から S までの頂点エッジの重みが最小になります。このエッジを ek+1={ik+1 ,il} とし、ek+1∈T であれば、アルゴリズム ステップ k+1 は明らかに正しいです。
T に ek+1 が含まれていないと仮定すると、T に ek+1 を追加してループを形成します。このループには、S と VS の頂点のエッジ e を接続する中間頂点の別のエッジ e があります。T
*=(T-{e})∪{ek+1} とすると、Tは G のスパニング ツリーです。 e1 ,e2,…ek+1 を含む W(T)<=W(T ) アルゴリズムでも、ステップ k+1 で最小スパニング ツリーが得られます。
上記の Prim アルゴリズムでは、条件を効果的に見つける方法も考慮する必要があります。 iS、jVS、および最小の重みを持つエッジ (i, j) c。この目的を達成するためのより簡単な方法は、最も近くにある 2 つのアレイを低コストでセットアップすることです。
プリムのアルゴリズムの実行中、まず、VS で lowcost 値を最小化する頂点 j を見つけ、次に最も近い配列に従ってエッジ (j,most[j]) を選択し、最後に j を S に追加し、最も近い値と lowcost に必要な変更を加えます。。
このように実装された Prim のアルゴリズムに必要な計算時間は です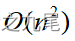
。
2.3 クラスカルアルゴリズム
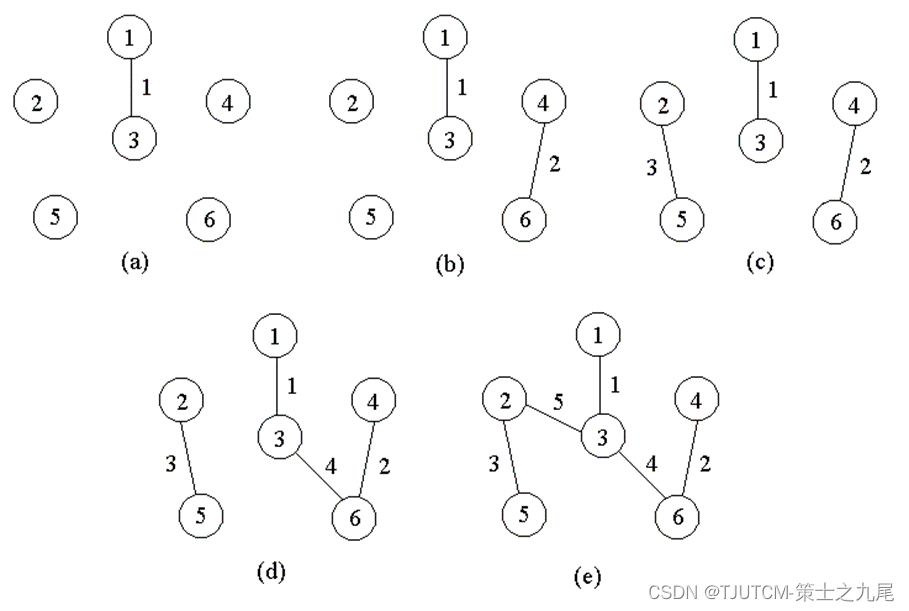
G の最小全域木を構築するクラスカルのアルゴリズムの基本的な考え方は、まずG の n 個の頂点を n 個の孤立した接続された枝として扱うことです。すべてのエッジを小さいものから大きいものに並べ替えます。次に、最初のエッジから始めて、エッジの重みが増加する順に各エッジを表示し、接続された 2 つの異なるブランチを次のように接続します。k 番目のエッジ (v, w) を見るとき、端点 v と w がそれぞれ現在の 2 つの異なる接続されたブランチ T1 と T2 の頂点である場合、エッジ (v, w) を使用して T1 と T2 を A に接続します。接続されたブランチを確認し、引き続き k+1 番目のエッジを確認します。；エンドポイント v と w が同じ接続されたブランチ内にある場合は、k+1 番目のエッジを直接チェックします。。このプロセスは、接続されたブランチが 1 つだけ残るまで続きます。
たとえば、前の接続された重み付きグラフの場合、クラスカル アルゴリズムに従って取得された最小スパニング ツリー上のエッジは、次の図に示されているようになります。
命題:任意の n に対して、アルゴリズムは n 次グラフの最小スパニング ツリーを見つけます。
2.3.1 証明のアイデア
帰納的基本証明: n=2、アルゴリズムは正しい。G にはエッジが 1 つだけあり、最小スパニング ツリーは G です。
帰納法ステップの証明: アルゴリズムが n 次のグラフ (n>1) に対して正しいと仮定すると、アルゴリズムは任意の n+ に対する最小スパニング ツリーも取得します。 1 次グラフ 短絡演算:
任意 n+1 個の頂点を持つグラフ G が与えられると、G の最小エッジの重みは e={i,j} となり、G から i と j をマージし、グラフ G を取得します。 '
2.3.2 誘導ステップ耐性
任意の n+1 次グラフ G について、最短エッジ e を短絡することにより、n 次グラフ G' が得られます。帰納的仮説アルゴリズム に従って
、G' の最小全域木 T' が得られます。
短くなったエッジ e を元の長さに戻すと、ツリー T が得られます。
これは、T が G の最小スパニング ツリーであることを証明します。
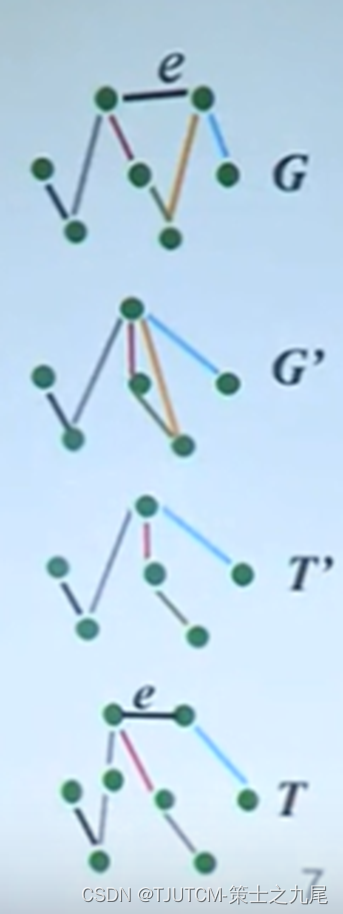
2.3.3 T は G の最小スパニング ツリーです
T=T'∪{e} は G に関する最小全域木です。それ以外の場合は、
G のエッジ e を含む最小全域木
T*が存在します、W(T*)<W(T)。(e が T* に属していない場合は、エッジ e をTに追加してループを形成します。ループ内の他のエッジをすべて削除しても、結果として得られるスパニング ツリーの重みは依然として最小になります。) T で e を短絡してスパニング ツリーを取得します。 G' の T*-{e}、
W(T*-{e})=W(T*)-w(e)<W(T)-w(e)=W(T')、最適性と矛盾T'の
セットに対するいくつかの基本的な操作を使用して、クラスカルのアルゴリズムを実装できます。
重みの昇順に表示することは、優先キューに対して RemoveMin 操作を実行することと同じです。この優先キューは、ヒープを使用して実装できます。
接続されたブランチで構成されるセットを継続的に変更するには、抽象データ型と UnionFind でサポートされる基本操作を使用する必要があります。
グラフの辺の数が e の場合、クラスカルのアルゴリズムで必要な計算時間は次のとおりです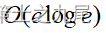
。
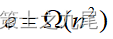当時、クラスカルのアルゴリズムはプリムのアルゴリズムよりも劣っていましたが
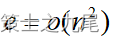、当時はクラスカルのアルゴリズムがプリムのアルゴリズムよりもはるかに優れていました。
2.4 応用: データのグループ化の問題
一連のデータ (写真、文書など) を相関関係に従って分類する必要があります。
類似度関数または「距離」を使用して、個人間の違いを説明します。
それらはいくつのカテゴリに分割する必要がありますか? 各カテゴリ内の個人を可能な限り近づけ、異なるカテゴリ間の個人を可能な限り「遠く」にします。分割方法は？
2.5 シングルチェーンクラスタリング
クラスカルのアルゴリズムに似ています。
エッジの長さの昇順でエッジをソートし、
現在の最短エッジ e を調べます。e が選択したエッジとループを形成しない場合は、e をセットに追加し、それ以外の場合は e をスキップします。
k 個の接続されたブランチが保持されるまで、グラフの接続されたブランチの数をカウントします。
3. マルチマシンのスケジューリングの問題
マルチマシンのスケジューリング問題では、指定された n 個のジョブを m 台のマシンで最短時間で処理できるようにジョブ スケジューリング プランが必要です。
各ジョブはどのマシンでも処理できることが合意されていますが、完了する前に処理を中断することは許可されません。ジョブをより小さなサブジョブに分割することはできません。
この問題は NP 完全であり、今のところ効果的な解決策はありません。このタイプの問題では、貪欲な選択戦略を使用して、より適切な近似アルゴリズムを設計できる場合があります。
マルチマシンのスケジューリング問題を解決するためのより適切な近似アルゴリズムは、処理時間が最も長いジョブを優先する貪欲な選択戦略を使用して設計できます。
この戦略によれば、
のとき、マシン i の [0, ti] 時間間隔をジョブ i に割り当てるだけで、アルゴリズムに必要な時間は O(1) だけです。
この
とき、まずn個のジョブを処理時間に応じて大きいジョブから小さいジョブに分類します。その後、ジョブはこの順序でアイドル状態のプロセッサに割り当てられます。このアルゴリズムに必要な計算時間は O(nlogn) です。
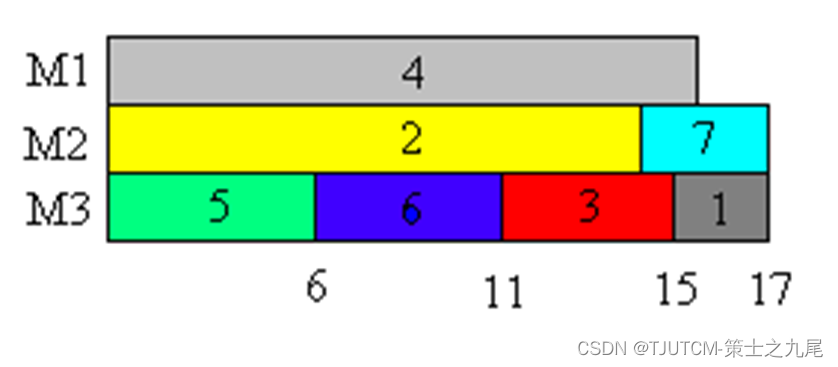
たとえば、7 つの独立したジョブ {1、2、3、4、5、6、7} が 3 台のマシン M1、M2、M3 によって処理されるとします。各ジョブに必要な処理時間はそれぞれ {2,14,4,16,6,5,3} です。貪欲アルゴリズムによって生成されたジョブ スケジュールは次の図に示されており、必要な処理時間は 17 です。
4. まとめ
貪欲なアルゴリズム通常、最適解を見つけるために使用され、
常に現在の状況で局所的な最適解を選択し、順番に処理を進めて全体的な最適解を取得します。
現在の最良の選択は通常、見つけやすい貪欲なアルゴリズムです
。正しさを証明する必要があります。数学的帰納法が一般的に使用されます。
最初のステップは明らかな
帰納ステップです。通常、矛盾によって証明され、反例を与えることで反証されます。