1. 小さなアルゴリズムの魅力

これは非常に一般的な小さな例ですが、改良されたアルゴリズムの強力な魅力を理解することができます。

Known a+b+c = 1000、およびa^2+b^2=c^2a、b、c のすべての自然数解を求めます。
これは非常に簡単です。つまり、コードを通じて a、b、c に値を代入し、とa+b+c = 1000に一致する解を返すだけですa^2+b^2=c^2。
以下に、リファレンスコードの 2 つのセクションを示します。
最初のセクションでは、1 ～ 1000 を走査し、一般的な試行錯誤ロジックに従って値を a、b、c に割り当て、その後 3 つの値を取り出しますif a + b + c == 1000 and a**2 + b**2 == c**2。条件を満たすもの。

# 代码1：
import time
start_time = time.time()
for a in range(1,1001):
    for b in range(1,1001):
        for c in range(1,1001):
            if a + b + c == 1000 and a**2 + b**2 == c**2:
                print('a:%d, b:%d, c:%d'%(a,b,c))
end_time = time.time()
print('程序总用时：%f'%(end_time-start_time))

コード1の実行結果は下図の通りで、今回の実行時間は951.8秒でした。
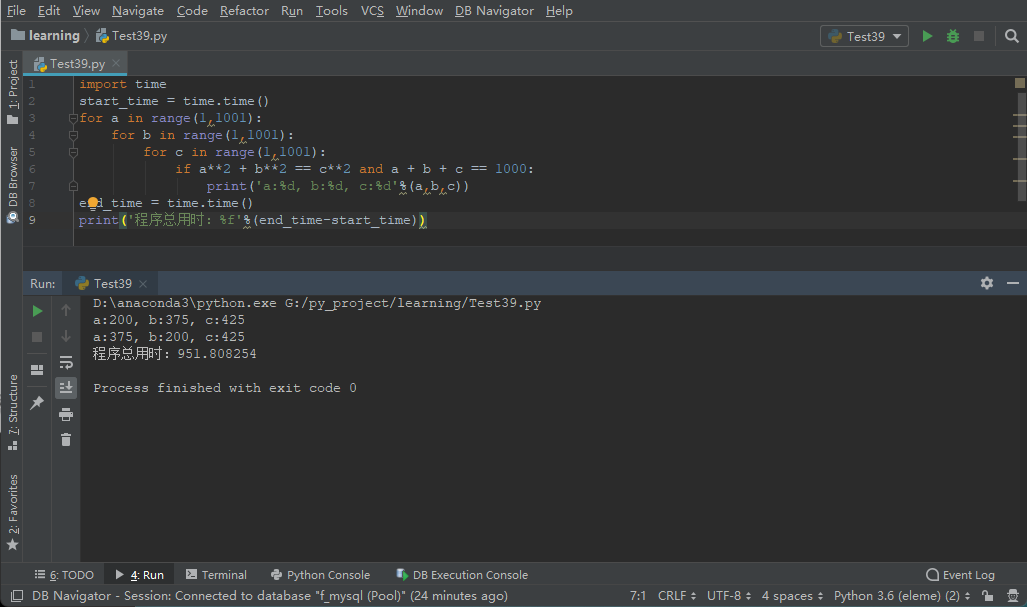
画像.png

もう一度コード 2 を見てみましょう。コード 1 に基づいて小さな変更が加えられています。1 ～ 1000 を 2 回トラバースするだけで、3 番目の数値は 1000 から最初の 2 つの数値を引くことによって取得されます。コードは次のとおりです。 :

# 代码2：
import time
start_time = time.time()
for a in range(1,1001):
    for b in range(1,1001):
        if a**2 + b**2 == (1000-a-b)**2:
            print('a:%d, b:%d, c:%d'%(a,b,1000-a-b))
end_time = time.time()
print('程序总用时：%f'%(end_time-start_time))

コード 2 の実行結果を次の図に示します。今回のコードの実行には 1.4 秒しかかからないことがわかります。
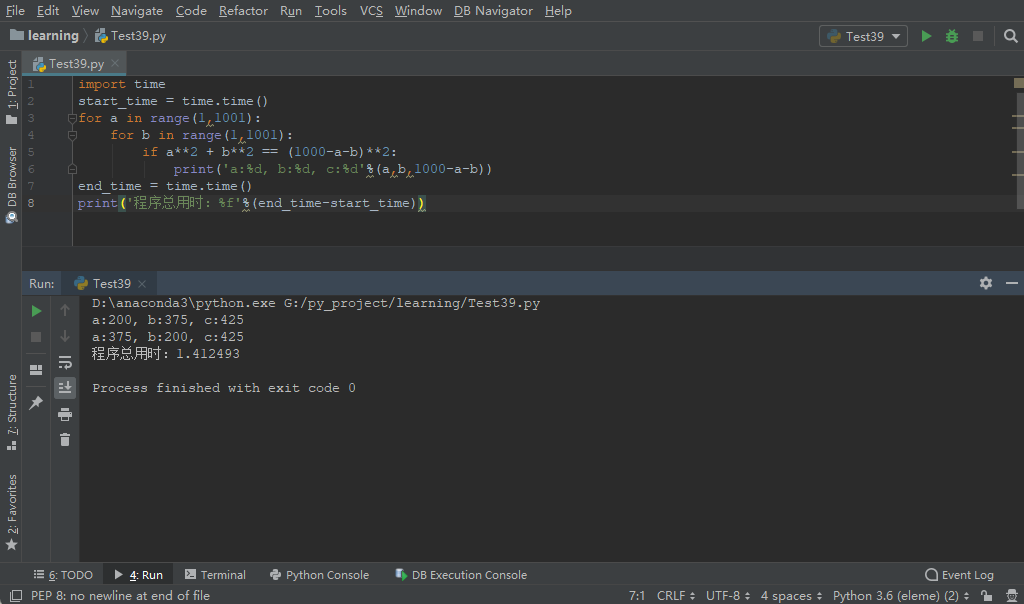
画像.png

上記 2 つのコードの実行結果から、両者の時間差は約 700 倍であることがわかります。コード 1 をコード 2 に置き換えると、各実行の待ち時間が約 16 分短縮され、特に優れたエクスペリエンスが得られます。

アルゴリズムのちょっとした魅力を感じたところで、アルゴリズムの複雑さについて簡単にお話しましょう。

2. 複雑さ

複雑性は一般に、時間複雑性と空間複雑性の 2 つのタイプに分類されます。
時間計算量は主にアルゴリズムの実行速度を測定し、空間計算量は主にアルゴリズムに必要な追加スペースを測定します。コンピューター開発の初期には、コンピューターの記憶容量は非常に小さかったです。そのため、私は空間の複雑さを非常に懸念しています。しかし、コンピュータ産業の急速な発展に伴い、コンピュータの記憶容量は非常に高いレベルに達したため、アルゴリズムの空間の複雑さに特別な注意を払う必要はなくなり、アルゴリズムの時間の複雑さにもっと注意を払うようになりました。

2.1 時間計算量

時間計算量は漸近時間計算量でもあり、公式の定義は次のとおりです:
n が無限大に近づくような関数 f(n) がある場合、 $T (n) / f (n)$ と呼ばれます。 $f (n)$ です $T (n)$ と同じ桁の関数書きます $T (n) = O (f (n))$ ，称 $O (f (n))$ はアルゴリズムの漸近的な時間計算量であり、時間計算量と呼ばれます。
漸近的な時間計算量は大文字の O で表現されるため、ビッグ O 表記法とも呼ばれます。などの一般的な表現方法 $O (1)$ 、 $O (l o g n)$ 、 $O (n)$ 、 $O (n l o g n)$ 、 $O(n^2)$ 、 $O(n^3)$ 、 $O(2^n)$ など
一般に、複雑さが小さいほど、コードは優れています。複雑さは次のとおりです:
$O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O (n^3) <O(2^n)<O(n!)<O(n^n)$

時間計算量を計算するとき、理論的には、時間のかかるすべての操作を考慮する必要があります。たとえば、要素がすべて長い文字列であるリストを走査して等しい文字列を見つけるには、文字列の走査の実行時間に加えて文字も考慮する必要があります。 . 文字列比較 (以下の例)。

for i in ['abc','bcd','cde']:
    if i == 'cde':
        print(i)

一般的な基本コード、他のオブジェクトの呼び出しがないコードは定数項目であり、複数回実行しても数行にnなる; シーケンスの長さに応じてトラバーサルループが定義されるn. は $2 * n$ 、ネストされた走査を 2 回行うと、 $n^2$ 。

ただし、実際の申請プロセスでは、時間の複雑さは一般に単純化され、最も影響力のある要素に注目するだけであることが多くなります。

2.2 時間計算量の単純化

時間計算量を比較する場合、通常は次の方法を使用して計算量を単純化して比較します。

などのO(1)表現を使用すると、複雑度は一定です。 $O (23)$ ， $お (9999)$ ；
複雑度に n が含まれる場合は、次のように係数と定数項を省略します $\longrightarrow O(n)$ ；
複雑度が対数の場合、次のようにO(logn)表されます: $log_5 n$ 、 $log_2n$ ；
$O(4n^3+6n^2+n) \longrightarrow O(n^3 など) のように高次のみを取得し$ ます。 $O (4n_^{3} + 6n_^{2} + n) ⟶ O (n^{3})$ 。

如： $ログン___+ n l o g n$ で表されます。 $O (n ログ n)$ 。 $_$ $_$

時間計算量を比較する場合、定数項、低次項、高次項、対数の底の係数は通常無視されます。と言ってください。 $O (2n_+ 1)$ 简化为O(n) ， $O(2*n^3+5n^2+5)$ $O(n^3)$ に簡略化します。 $O (n^{3})$ ， $O(log_2n)$ に簡略化されます $O (ログ n)$ . $_$ $_$ 記事の冒頭にある 2 つのコード文字列の複雑さは $O(n^2)$ 和 $O(n^3)$ 。

2 つの質問:
1. 定数項、低次項、係数が無視されるのはなぜですか?

ビッグ O は実際には、データレベルがある点を突破し、データレベルが非常に大きいときに示される時間計算量であるため、この点の定数項、低次項、および係数は決定的な役割を果たしません。

2. O(logn) が対数の底を区別しないのはなぜですか?

対数は、他の底の対数を乗じた定数に変換できるため、 $log_2 16=log_{10} 16 /log_{10} 2 \iff log_{10} 16 = log_{10} 2 * log_2 16$ (16 を n と考えると、次の理解が容易になります)、したがって、 $\ left( log_2n \right)=log_2 10*O \left(log_{10}n \right) \iff O \left(log_i n \right)=log_i j*O \left(log_jn \right)$ 故 $\left(log_i n \right) \implies O \left(log_jn \right) \implies O \left(logn \right)$ 。 $_$ $_$ $_$

2.3 共通機能の複雑さ

共通機能	ビッグオー
[n]、インデックス	○(1)
追加()	○(1)
ポップ（）	の上）
入れる（）	の上）
の	の上）
反復	の上）
含む（）	の上）
[m,n] スライス	オ(メートル)
スライスの	の上）
スライスを設定する	O(n+m)
逆行	の上）
連結する	オ(メートル)
選別	O(n log n)
かける	O(n*m)
コピー	の上）
アイテムを入手する	○(1)
セットアイテム	○(1)
アイテムの削除	○(1)
を含む(n)	○(1)
反復	の上）

3. まとめ

1. 一般に、時間計算量を比較する場合、単純化して比較するために次の方法が使用されます。

などのO(1)表現を使用すると、複雑度は一定です。 $O (23)$ ， $お (9999)$ ；
複雑度に n が含まれる場合は、次のように係数と定数項を省略します $\longrightarrow O(n)$ ；
複雑度が対数の場合、次のようにO(logn)表されます: $log_5 n$ 、 $log_2n$ ；
$O(4n^3+6n^2+n) \longrightarrow O(n^3 など) のように高次のみを取得し$ ます。 $O (4n_^{3} + 6n_^{2} + n) ⟶ O (n^{3})$ 。

2. 複雑さが小さいほど、コードは優れています。複雑さは次のとおりです:
$O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n ^3) <O(2^n)<O(n!)<O(n^n)$

Pythonアルゴリズム：アルゴリズムの小さな魅力と複雑な計算を感じる