1. シンプレックス法は標準的な線形計画法に基づいています
2. 標準線形計画法の最適解は、実行可能領域の頂点になければなりません。
3. シンプレックス法は頂点上の最適解を探索します。
4. 修正シンプレックス法の反復ステップをマスターする
前回の記事では、探索アルゴリズムのロジックを詳しく紹介し、線形の目的と凸の実現可能集合を持つ最適化モデルの場合、局所的な最適解が大域的な最適解であるという結論を得ました。制約は実現可能領域の性質を決定します. 当然のことながら, 実現可能領域が凸集合であるという最も単純な条件を研究したいと思います. 次の原則があります:

最適化されたモデルのすべての制約が線形の場合、モデルの実現可能領域は凸型になります。
これを証明できます:

任意の 2 つの解を結ぶ線上の任意の点が制約条件を満たす、つまり、実現可能な集合が凸集合であることがわかります。
オペレーションズ リサーチの開始時に、モデル分類を導入しました。線形計画法 (LP)は、目的関数方程式と制約方程式の両方が決定変数に関するものであり、決定変数が連続である線形方程式です (それ以外の場合は整数計画法です)。 。線形計画法のこれらの特性はすべて、「局所最適解が大域最適解である」という探索アルゴリズムの条件を満たします。今日は、線形計画法モデル-シンプレックスの特定の検索アルゴリズムを紹介します。
1
標準的な線形計画法
シンプレックス法は、標準形式の線形計画法に基づいています。

線形計画法の標準形式は次の条件を満たします。
主な制約は等価制約です
変数はすべて非負です
主な制約の変数は等号の左側にあり、各変数は最大 1 回出現し、定数は右側にあります。
これは、線形計画法の一般的な記述方法とは異なります。主な制約は方程式になっています。スラック変数を導入することで不等式を方程式に置き換えます。例を示します。
高級真鍮製トロフィーを扱う架空の会社が直面する問題を考えてみましょう。同社は青少年スポーツリーグ向けの大きなトロフィーを製造しています。現在、秋の試合(サッカー、ラグビー)に向けた制作を計画している。各フットボール トロフィーは木製の台座、刻印されたネームプレート、真鍮製のフットボールで構成されており、各トロフィーは会社に 12 ドルの利益をもたらします。フットボールのトロフィーも同様ですが、上部に真鍮製のフットボールがあり、各フットボール トロフィーは 9 ドルの利益しか貢献できません。フットボールの形状が非対称であるため、そのベースには 4 平方フィートの木材が必要ですが、フットボールのベースには 2 平方フィートしか必要ありません。同社が現在保有している在庫には、真鍮製サッカーボール 1,000 個、真鍮製サッカーボール 1,500 個、名札 1,750 個、および 4,800 平方フィートの木材が含まれています。作成したすべてのトロフィーを販売できると仮定すると、企業は利益を最大化するためにどのようなトロフィーの組み合わせを作成する必要がありますか?

真鍮のトロフィー問題は、最適化モデルを簡単に作成できます。

これは変数が 2 つだけの線形計画法モデルで、高校で習う線形計画法であるグラフィカルな手法を使えば簡単に最適解 x1=650、x2=1100 を求めることができます。さらに多くの変数がある場合、グラフィカルな方法は実行できなくなります。新しい方法を見つけなければなりません。
線形計画法の場合、その実現可能領域は凸集合であり、その場合、最適解は実現可能領域の境界上になければなりません。それ以外の場合、 c が a でない限り、目的関数式 cx に従って、点は内部点になります。一定である場合、実現可能な改善の方向性を見つけることができます。さらに、最適解は実行可能領域の頂点になければなりません。これを証明します:

注:境界、頂点、および内部点には厳密な数学的定義があり、それは最後に示します。関連するナレッジはデフォルトですでに利用可能です。
ここまで、シンプレックス法の核心である、実行可能領域の頂点での最適解の探索を紹介しました。
頂点の場合、対応する制約は厳密制約である必要があるため、不等式制約を等式制約に変更する、つまり標準的な線形計画法に変換する必要があります。主要なポイントは 2 つあり、1 つ目はスラック変数を導入することです。
線形計画モデルの主要な不等式制約は、係数に影響を与えない非負のスラック変数を追加することで等式制約に変換できます。 ≤ 制約はこれらの変数を加算し、 ≥ 制約はこれらの変数を減算します。

真鍮のトロフィーを例として、上記の最適化モデルを標準タイプに変更してみましょう。
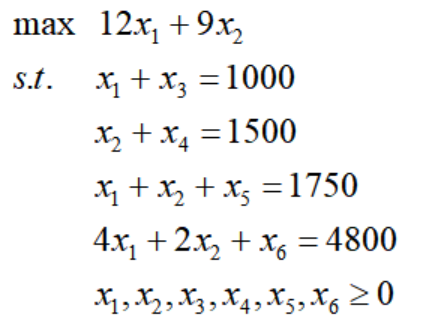
標準の線形計画法に変換する 2 番目のポイントは、非正および符号なしの必須変数を非負に変換することです。非正の変数は負の値に置き換えることができ、符号要件のない変数 (URS) は差分に置き換えることができます。 2 つの非負変数間の値表現。
例えば:
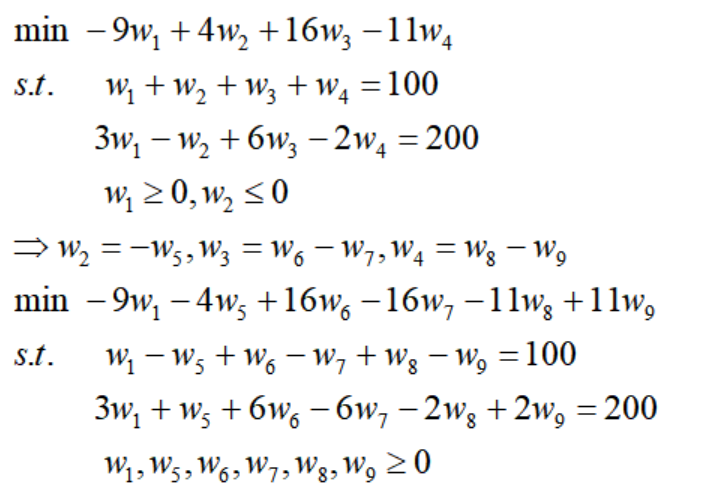
したがって、すべての線形計画問題は標準形式の線形計画問題に変換でき、行列表現が導入されます。標準形式の LP は次のように記述できます。
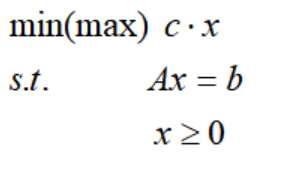
2
基本的な実現可能な解決策
標準線形計画法 (LP 標準) が実際には線形方程式の解であることがわかります。高度な代数の知識によれば、線形方程式には一意の解が存在する場合もあれば、解が存在しない場合もあれば、無限に多くの解が存在する場合もあります。ここでのシーンと組み合わせると、LP 標準タイプの解が実行可能領域の頂点上にあり、各頂点が一意であることがわかります。そのため、次のように再定義します。
線形計画法標準形式の基本的な解は、いくつかの変数値を 0 に設定することによって得られるため、他の変数値は等式制約を通じて一意に解くことができます。0 に設定された変数は非基本変数と呼ばれ、等式制約によって解決される変数は基本変数と呼ばれます。

ここには、一意の解というキーワードがあります。これは、特定の変数を 0 に設定した後の方程式系が唯一の解であることが保証され、基本解に属することが保証されなければならないことを意味します。プレミアム真鍮トロフィーケースを例に挙げます。
変数 x5 と x6 を非基本変数として設定すると、方程式系は次のようになります。

ただし、非基本変数のセットが基本解を取得できるわけではないことに注意してください。たとえば、x4=0 のみの場合、方程式系は次のようになります。
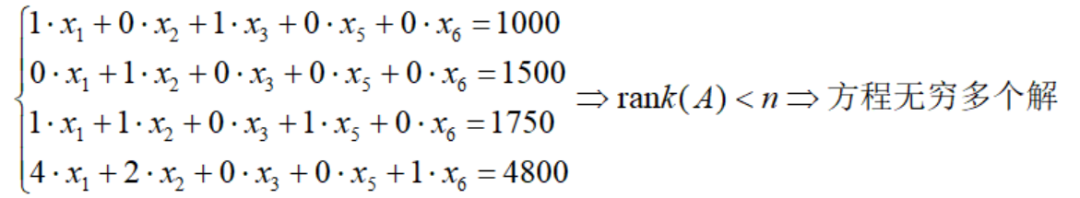
係数行列のランク r は変数の数 n より小さくなければならず、方程式の解は無限にあり、基本的な解は得られないことがわかります。明らかに、根本的な解決策が存在する状況を見つける必要があります。高度な代数の知識によれば、次のことが簡単に得られます。
基本的な解決策は、基本変数に関連付けられた等式制約が、モデルに存在する線形独立制約の最大セットに由来する場合にのみ存在します。
この文は少しわかりにくいですが、ガオ ダイの表現に置き換えるとすぐに理解できます。

つまり、標準形式の係数行列から、同じ次元と基本変数に関連する等式制約の数を持つ線形独立列ベクトルで構成される行列を見つけるだけで十分です。
一般に、列ベクトルの次元は等式制約の数と等しいと想定します。このように、上級ブラストロフィーの場合、非基本変数の数は 2 に固定され、基本変数の数は 4 になります。基本変数として係数行列の 4 つの線形独立列ベクトルの組み合わせを求めます。 :
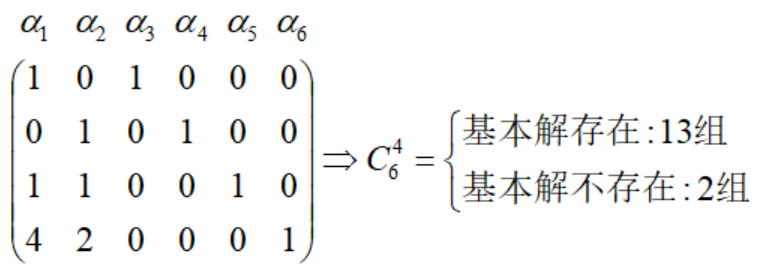
線形独立した列ベクトルの組み合わせが 13 セットあり、方程式には固有の解が存在します。解は以下にリストされています。
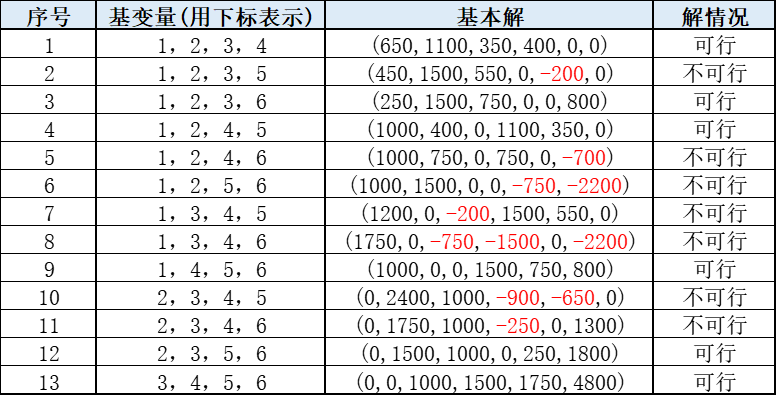
赤い部分は、対応する変数が非負の制約を満たしていないことを示します。したがって、対応する解は基本的な解ではありますが、実行不可能ではありません。明らかに、私たちの目標は、基本的な実行可能な解決策を見つけることです。
線形計画法標準形式の基本的な実現可能な解は、すべての非負性制約を満たす基本的な解です。
等式制約によって得られる点はすべて実行可能領域の頂点上にあるため、基本的な実行可能解は実行可能領域の頂点になります。
3
初等シンプレックス法
基本的な実現可能解を通じて実現可能領域内の頂点を特定するシンプレックス法は、頂点での探索アルゴリズムであり、次のステップは当然、頂点から隣接する頂点まで探索することになります。隣接する頂点を決定するタイト制約グループでは 1 つの制約のみが異なるため、これら 2 つの頂点を接続する各エッジは、対応するタイト制約グループ内の共通の制約によって決定されます。そして、基本的な実現可能解 ここでの厳しい制約は、非基本変数の非負制約のみであるため、単体方向は、非基本変数の非負制約を順次緩和することによって取得されます。1 つの基本的な実行可能なソリューションから次の基本的な実行可能なソリューションまで、すべての制約が満たされる必要があります。つまり、次のとおりです。
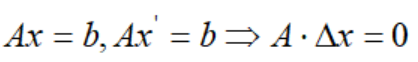
したがって、単体方向は、一次一次方程式系を解くことによって取得できます。以下に例を示します。
高度な真鍮トロフィーの場合、基本的な実行可能な解 x=(0,0,1000,1500,1750,4800) があり、x1 と x2 のいずれかを増加させるとシンプレックス方向を取得できます。x1 を 1 ずつ増加させ、次の等次方程式を解いて単体の方向を取得します。
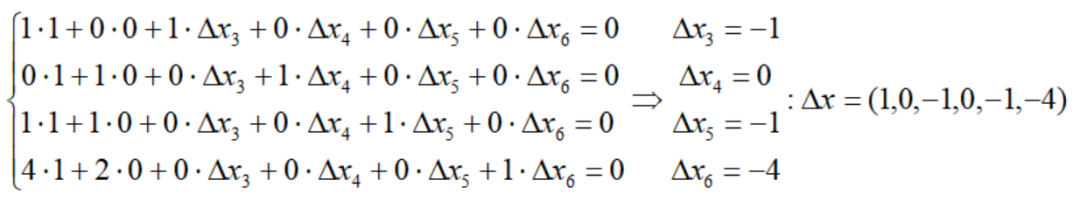
さらに、目的関数の変化する値を取得します。

次に、ステップ サイズが残ります。単体方向は等式制約を満たすため、ステップ サイズを制限できるのは非負制約のみです。単体方向の変数が負の場合のみ、条件は満たされないため、必要なのは Just最小の臨界点に移動します。

このようにして、一次シンプレックス法 (5A アルゴリズム)が得られます。

ここで、 「ベース内へ」と「ベース外へ」の概念を説明する必要があります。各反復で、0 に等しい変数はアウトベースであり、0 に等しくない変数はインベースです。文字 B は基本変数を表すために使用され、N は非基本変数を表します。
高級真鍮トロフィーのケースを例として、5A アルゴリズムのプロセスを見てみましょう。
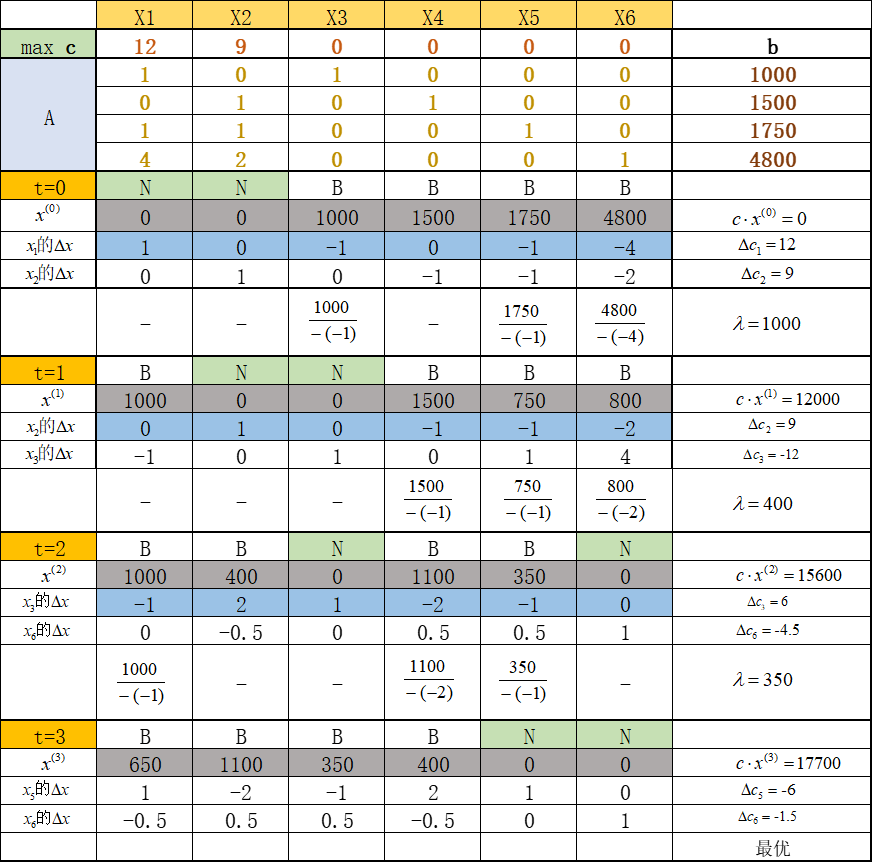
t=0 の場合、非基本変数 x1 と x2 は 2 つの単体方向を取得します。明らかに、方向 1 を選択すると、さらに最適化が可能になり、最終的にステップ サイズが決定されます。t=1 の場合、非基本変数は x2 と x3 です。この時点では、最適化された単体方向は 1 つだけであるため、t=3 まで繰り返します。最適化された単体方向は存在しなくなるため、反復を停止します。
4
修正シンプレックス法
基本シンプレックス法はアルゴリズムの論理を重視していますが、計算効率が低く、行列計算に変換できればさらに効率が良くなるはずです。これは、プライマリ シンプレックス メソッドの改良版です -改訂されたシンプレックス アルゴリズム (改訂されたシンプレックス アルゴリズム)
まず、基本変数に対応する係数ベクトルで構成される行列を基本行列 (基本行列)として定義し、 B とします。
たとえば、上級ブラス トロフィーの t=1 リンクでは、基本変数に対応する基本行列は次のとおりです。
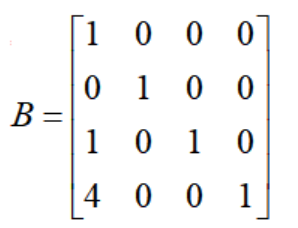
基本行列 B の列ベクトルはすべて線形独立であるため、フルランクであり、その逆行列が存在する必要があります。次の原則があります。

引き続き高度な真鍮トロフィー t=1 リンクを例として取り上げます。この時点での基本ソリューションの基本ベクトル要素は次のとおりです。
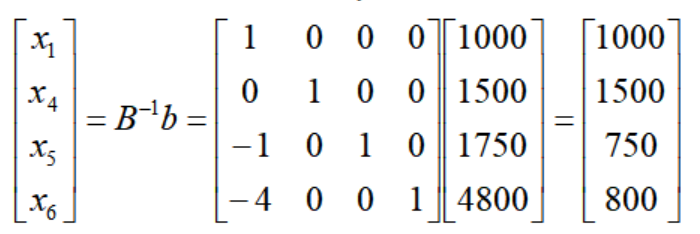
X2 の単体方向の基底ベクトル要素は次のとおりです。
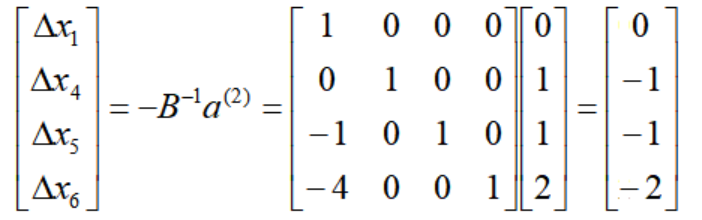
したがって、t=1 リンクの基本的な解決策とシンプレックス方向は次のとおりです。
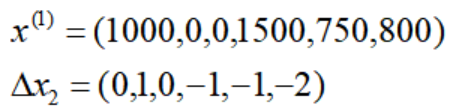
結果は一次シンプレックス法で計算した結果と同じです。
ベースインとベースアウトがあるため、基本行列は更新のたびに変更され、新しい基本逆行列と古い基本逆行列の間には関係があります。
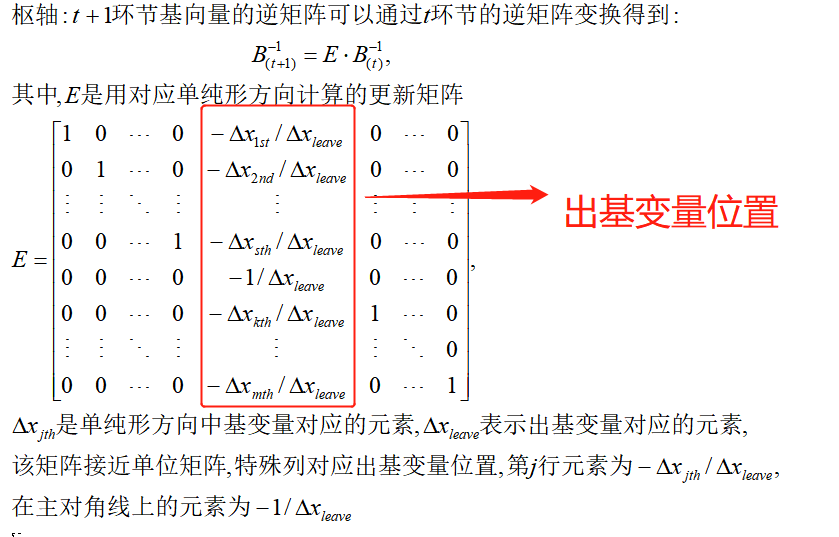
上級真鍮トロフィー t=1 リンクを例にとると、この時点の E は次のとおりです。

t=2 リンクでは、基底の逆行列が次のように更新されます。
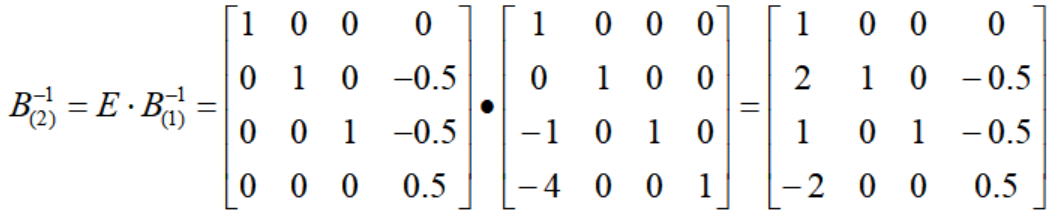
つまり、t=2 リンクの基底行列は次のようになります。
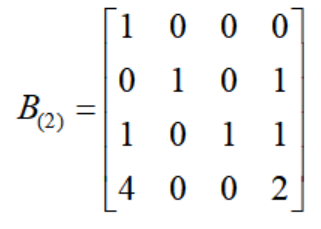
一見すると、一次シンプレックス法の t=2 リンクの基本行列とは異なります。t=1 から t=2 までは、基本外変数が X6、基本内変数が X2 であるためです。 、および t=2 リンクの基本行列。最後の列ベクトルは X2 を表します。つまり、次のルールに従います。
修正されたシンプレックス方式では、ベース内の入力変数の順序は、交換される出力変数と同じです。
最後に、目的関数の値の変化を考慮します。明らかに、2 つの隣接するリンクの目的関数の変化値は、非基本変数移動ユニット 1 の場合に確立されるシンプレックスの方向に関連しているため、次の値を簡単に取得できます。

高級真鍮トロフィーを例として、t=1 で取り上げます。
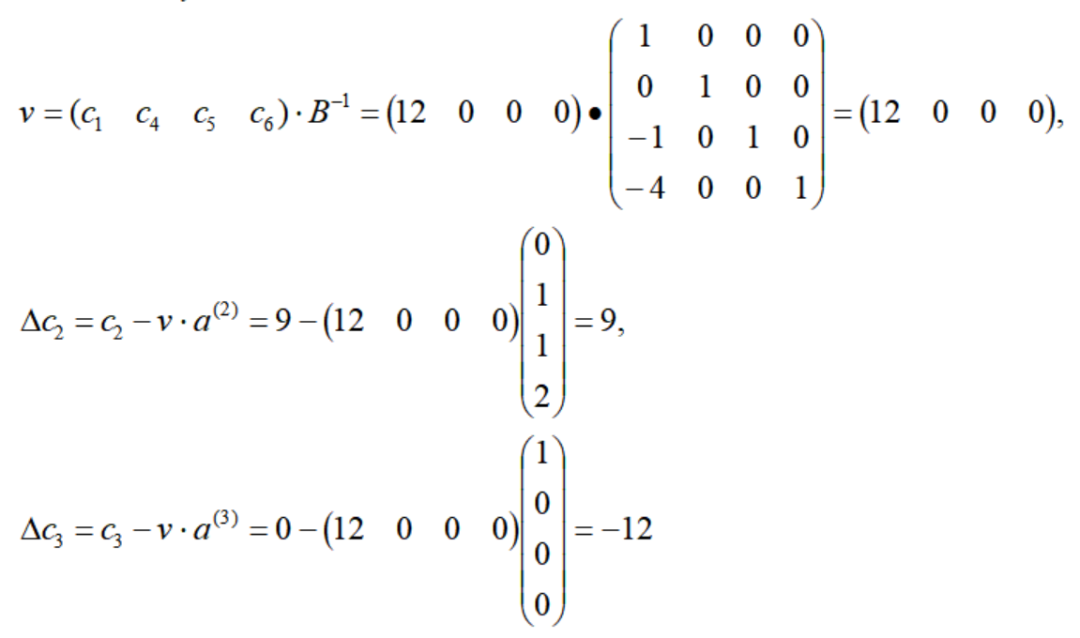
これまでのところ、修正されたシンプレックス法の具体的な手順を取得しました。

修正シンプレックス法を使用して、高レベルの真鍮トロフィーのケースを見てみましょう。プロセスは次のとおりです。
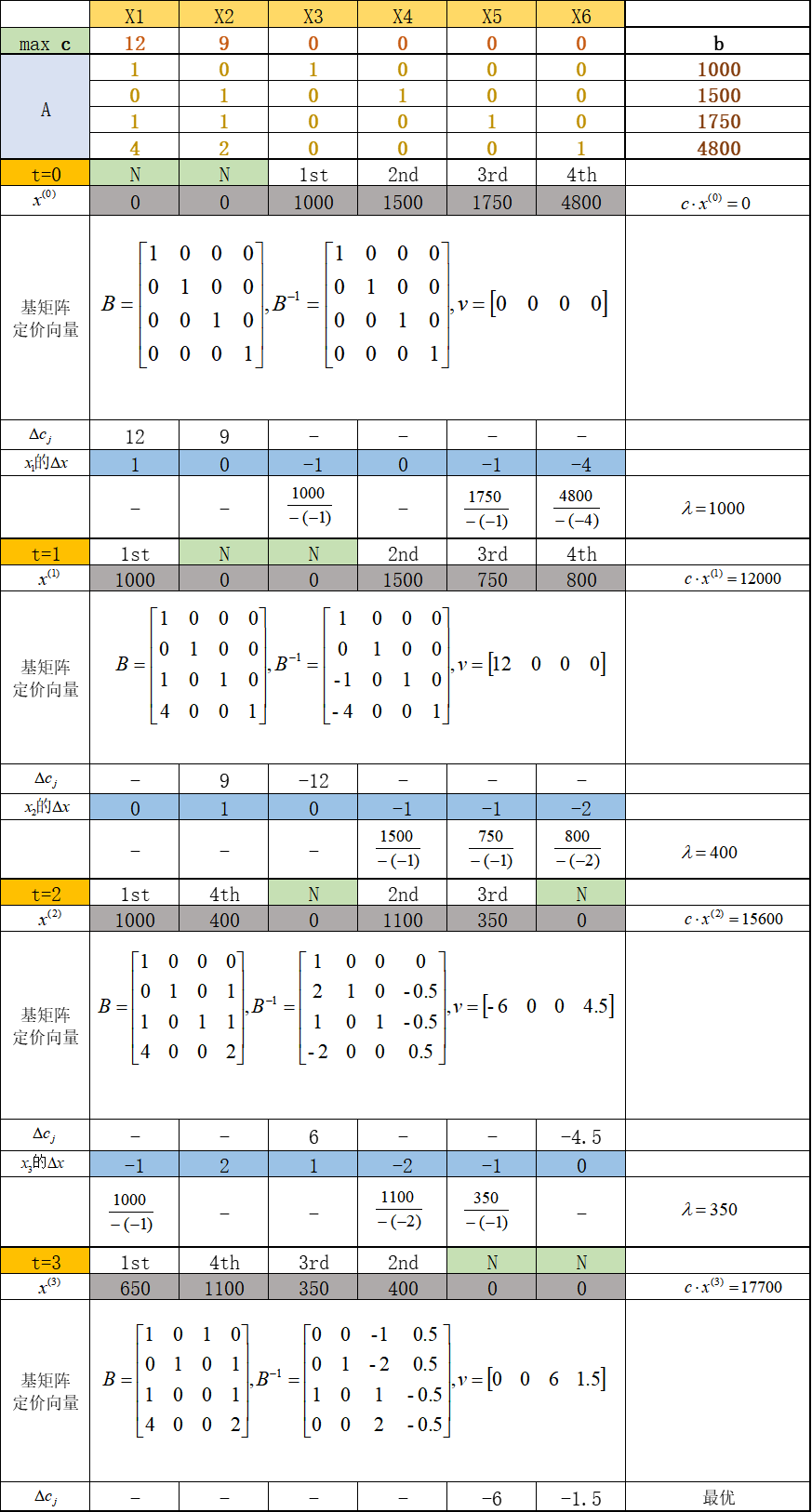
以上が修正シンプレックス法の反復処理である。
最後に、シンプレックス法では縮退の問題が発生する可能性がありますが、これについてはここでは説明しませんが、一般にシンプレックス法の収束には限界があります。
付録:
#找出所有线性无关向量组
import numpy as np
import itertools as it
from numpy.linalg import det
arr = np.array([[1,0,1,0,0,0],
[0,1,0,1,0,0],
[1,1,0,0,1,0],
[4,2,0,0,0,1]])
for e in it.combinations(range(1,7),4):
a = np.vstack((arr[:,e[0]-1],arr[:,e[1]-1],arr[:,e[2]-1],arr[:,e[3]-1]))
if det(a) != 0:
print(e)