Cet article est écrit dans les propres notes d'étude de Beamforming
Dans un langage simple, le principe mathématique de l'affectation des faisceaux est introduit, et un simple exercice de simulation de code python est donné en même temps.
Ce dont nous allons discuter, c'est comment façonner le faisceau pour atteindre "où frapper où", afin que les ondes radio puissent frapper dans la direction spécifiée.
Le réseau d'antennes commun est ULA (Uniform Linear Array, Uniform Linear Array), comme illustré dans la figure suivante :
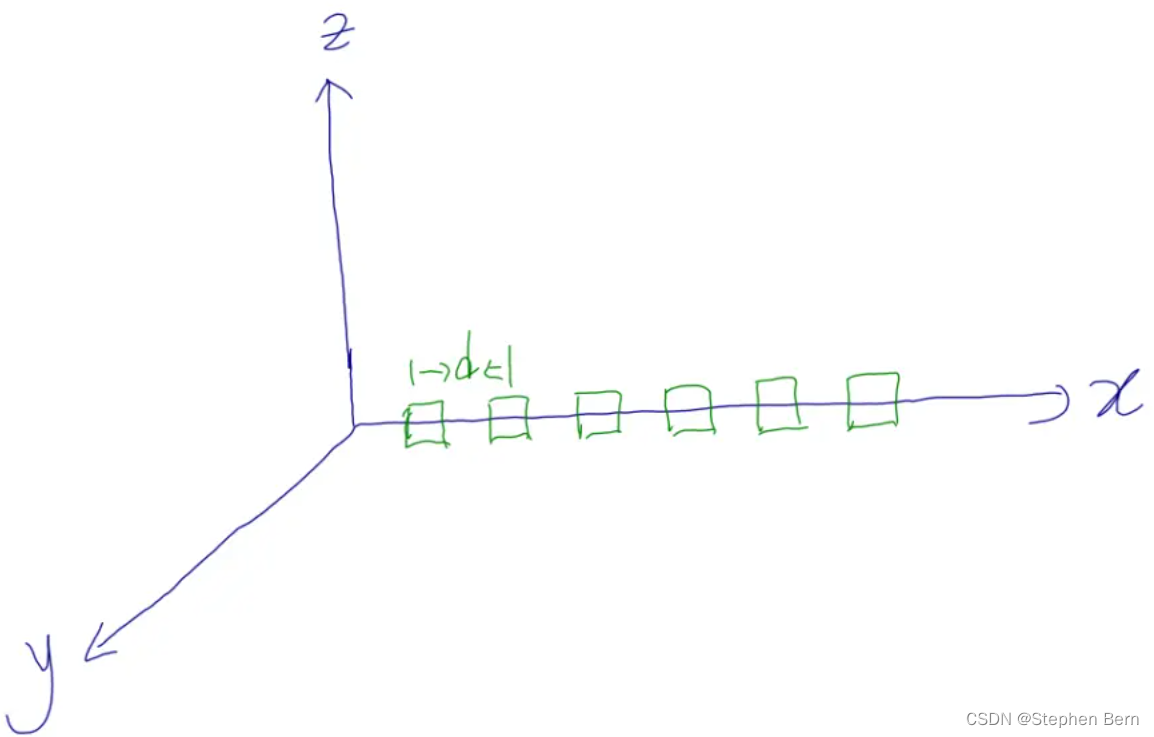
Un groupe d'antennes disposées uniformément horizontalement, la distance entre les antennes est enregistrée comme d.
Si l'atténuation du signal n'est pas prise en compte, les données de signal que nous transmettons sont s (un nombre complexe, avec amplitude et phase), et la distance entre l'extrémité de réception et l'extrémité de transmission est suffisamment éloignée, la connexion entre chaque antenne du extrémité émettrice et l'antenne unique de l'extrémité réceptrice, à partir de l'extrémité émettrice Le voisinage des antennes d'extrémité semble être parallèle (en fait, il n'est pas parallèle, mais presque parallèle, ce qui simplifie le calcul. S'il est pas simplifié, le calcul sera trop compliqué).
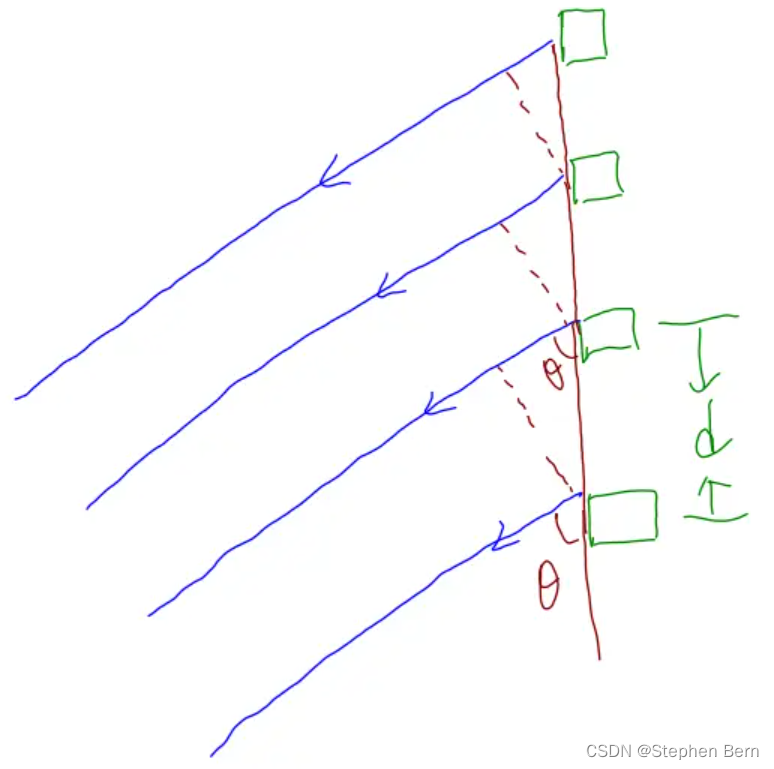
Supposons que l'angle entre la connexion du réseau d'antennes et la connexion de l'extrémité de réception est θ \thetaθEnsuite,
les signaux sans fil reçus par l'extrémité réceptrice à partir de différentes antennes émettrices auront des retards différents et auront donc des rotations de phase différentes
L'antenne émettrice au bas de la figure ci-dessus est utilisée comme référence. Nous choisissons l'antenne avec la distance en ligne droite la plus courte comme référence. Ensuite, les ondes radio transmises de la première antenne émettrice atteignent l'antenne réceptrice, et les ondes radio de la deuxième antenne émettrice à côté atteindra l'antenne réceptrice. Par rapport aux ondes radio émises par la première antenne émettrice, la distance parcourue est dcos ( θ ) dcos(\theta)d cos ( θ )
Alors l'onde radio émise par la kième antenne est( k − 1 ) dcos ( θ ) (k-1)dcos(\theta)( k−1 ) d cos ( θ )
Alors le temps supplémentaire est : la distance supplémentaire divisée par la vitesse de la lumière c
Δ t = ( k − 1 ) dcos ( θ ) c \Delta t=\frac{(k-1)dcos(\theta)}{c}∆t _=c( k−1 ) d cos ( θ ) .
En examinant l'onde électromagnétique à fréquence unique, en supposant que la fréquence est f, la déviation de phase due au temps de trajet supplémentaire est : 2 π
f Δ t = 2 π f ( k − 1 ) dcos θ c = 2 π ( k − 1 ) dcos ( θ ) λ 2\pi f\Delta t=\frac{2\pi f(k-1)dcos\theta}{c}=\frac{2\pi(k-1)dcos(\theta) }{ \lambda}2 p f D t=c2 π f ( k−1 ) d cos θ=je2π ( k _−1 ) d cos ( θ ) .
Forme : λ = cf \lambda=\frac{c}{f}je=Fcpour la longueur d'onde.
Tension aléatoire = 2 π dcos ( θ ) λ \psi=\frac{2\pi dcos(\theta)}{\lambda}p=je2 π ré cos ( θ )
Alors pour N antennes, les déphasages correspondants sont :
0 , ψ , 2 ψ , 3 ψ , . . . , ( N − 1 ) ψ 0,\;\psi, \;2\psi,\;3\psi,\;...,\;(N-1)\psi0 ,ps ,2ψ , _3ps , _... ,( N−1 ) p
Dans l'analyse du domaine fréquentiel, il est équivalent au signal émis bien que le signal de chaque antenne émettrice soit le même, mais le signal reçu par l'extrémité réceptrice est multiplié par :
ej 0 , ej ψ , ej 2 ψ , ej 3 ψ , . . . , ej ( N − 1 ) ψ e^{j0},\;e^{j\psi},\;e^{j2\psi},\;e^{j3\psi},\;..., \;e^{j(N-1)\psi}ej 0 ,ejψ , _ej 2 ψ ,ej 3 ψ ,... ,ej ( N - 1 ) p
Alors le signal reçu est :
1 N ∑ k = 0 N − 1 sejk ψ = s 1 N ∑ k = 0 N − 1 ejk ψ \frac{1}{N}\sum_{k=0}^{N- 1 }se^{jk\psi}=s\frac{1}{N}\sum_{k=0}^{N-1}e^{jk\psi}N1k = 0∑N - 1avec ejk ψ=sN1k = 0∑N - 1ejk ψ
Remarque : Diviser la formule ci-dessus par N correspond à la normalisation de l'énergie et n'affecte pas l'analyse des performances.
Alors le signal reçu est équivalent au signal émis, et sa variation est :
1 N ∑ k = 0 N − 1 ejk ψ \frac{1}{N}\sum_{k=0}^{N-1}e^{jk\psi}N1k = 0∑N - 1ejk ψ
Si seul le gain d'énergie est considéré, alors :
G ( ψ ) = 1 N ∣ ∑ k = 0 N − 1 ejk ψ ∣ G(\psi)=\frac{1}{N}|\sum_{k=0}^ { N-1}e^{jk\psi}|G ( ψ )=N1∣k = 0∑N - 1ejk ψ ∣
Après quelques dérivations (voir annexe), la formule ci-dessus peut se résumer ainsi :
G ( ψ ) = { ∣ sin ( N ψ / 2 ) N sin ( ψ / 2 ) ∣ , si ψ ≠ 0 1 , si ψ = 0 G (\ psi)= \begin{cases} |\frac{sin(N\psi/2)}{Nsin(\psi/2)}|, & \text {if $\psi \neq 0$} \\ 1 , & \text{if $\psi=0$} \end{cas}G ( ψ )={
∣N s dans ( ψ /2 )s dans ( N ψ /2 )∣ ,1 ,si p=0si p=0
ψ
= 2 π dcos ( θ ) λ \psi=\frac{2\pi dcos(\theta)}{\lambda}p=je2 π ré cos ( θ )
Après substitution, on peut calculer les différents gains correspondant aux différents angles à la réception , lorsque ψ \psiψ est0 0Lorsque 0 , prendre la valeur maximale, c'est-à-direθ = π 2 \theta=\frac{\pi}{2}je=2pou 3 π 2 \frac{3\pi}{2}215h _En prenant la valeur maximale.
programme Python, la courbe de gain tracée sur les coordonnées polaires est la suivante :
Supposons d λ = 1 2 \frac{d}{\lambda}=\frac{1}{2}jeré=21
La première image : 8 antennes d'affilée
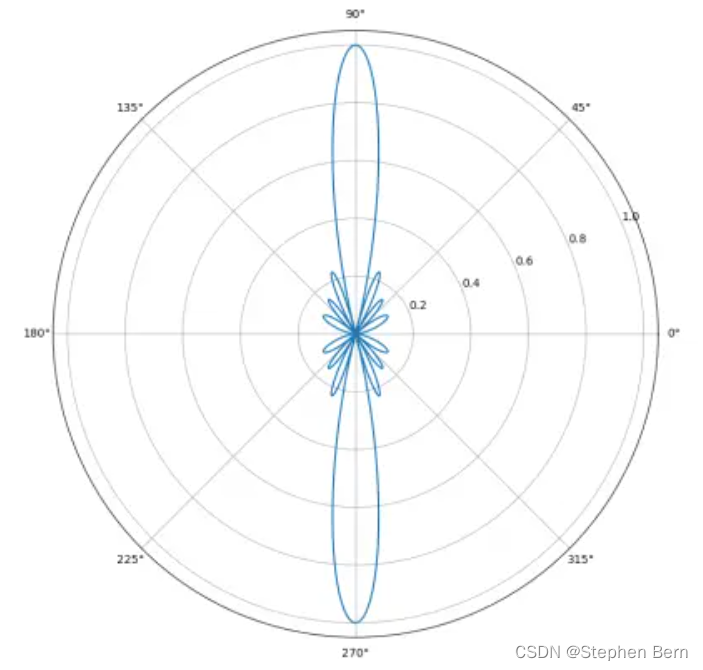
16 antennes en ligne

On peut voir que plus il y a d'antennes, plus le faisceau est concentré et étroit.
import numpy as np
from matplotlib import pyplot as plt
N = 8 #天线数量
theta = np.arange(0.000001,2*np.pi-0.0000001,0.01)
psi = np.pi * np.cos(theta)
r = np.abs(np.sin(N * psi/2)/np.sin(psi/2))/N
plt.figure()
plt.polar(theta,r)
plt.show()
Forme :
1 N ∑ je = 0 N − 1 ejk ψ = 1 N 1 − ej N ψ 1 − ej ψ = 1 N ej N ψ / 2 ej ψ / 2 ( e − j N ψ / 2 − ej N ψ / 2 ) ( e - j ψ / 2 - ej ψ / 2 ) = ej N ψ / 2 ej ψ / 2 sin ( N ψ / 2 ) N sin ( ψ / 2 ) \frac{1}{N}\sum_{ i=0}^{N-1}e^{jk\psi}=\frac{1}{N}\frac{1-e^{jN\psi}}{1-e^{j\psi}} =\frac{1}{N}\frac{e^{jN\psi/2}}{e^{j\psi/2}}\frac{(e^{-jN\psi/2-e^{ jN\psi/2}})}{(e^{-j\psi/2}-e^{j\psi/2})}=\frac{e^{jN\psi/2}}{e^ {j\psi/2}}\fraction{sin(N\psi/2)}{Nsin(\psi/2)}N1je = 0∑N - 1ejk ψ=N11−ejψ _1−ej N ψ=N1ej ψ /2ej N ψ / 2( e− j ψ /2−ej ψ /2 )( e− j N ψ /2 − ej N ψ /2 )=ej ψ /2ej N ψ / 2N s dans ( ψ /2 )s dans ( N ψ /2 )
Si seule la grandeur est considérée, des deux fractions dans la dérivation ci-dessus, le module de la première fraction est 1, ce qui peut être ignoré.
∣ 1 N ∑ k = 0 N − 1 ejk ψ ∣ = ∣ sin ( N ψ / 2 ) N sin ( ψ / 2 ) ∣ |\frac{1}{N}\sum_{k=0}^{N- 1}e^{jk\psi}|=|\frac{sin(N\psi/2)}{Nsin(\psi/2)}|∣N1k = 0∑N - 1ejk ψ ∣=∣N s dans ( ψ /2 )s dans ( N ψ /2 )∣