Einführung in Simpy: Python-Simulationsbibliothek-02/5

1. Beschreibung

        In Bezug auf die Simulationsbibliothek unter Python ist dieser Artikel der zweite Teil, der eine weitere Erläuterung des physikalischen Modells darstellt. Da dieser Teil des Inhalts stark auf der Symboleinführung im ersten Teil basiert, werden die folgenden Vorschläge bereitgestellt:

         Dieser Artikel ist der zweite Teil, wenn Sie den ersten Teil lesen . Es empfiehlt sich, sich den ersten Teil dieser Serie anzuschauen.

2. SymPy – Vereinfachung

 

        SymPy zeichnet sich durch die Vereinfachung mathematischer Ausdrücke durch seine vielfältigen Vereinfachungsfunktionen aus. In SymPy finden Sie die allgemeine Funktion Simply(), die darauf ausgelegt ist, die direkteste Darstellung eines Ausdrucks zu erreichen.

        Vereinfachung : Die Funktion simple(), die sich im Modul sympy.simplify befindet, wurde entwickelt, um Heuristiken zu verwenden, um die Einfachheit von Eingabeausdrücken zu verbessern. Ein Beispiel demonstriert seine Verwendung durch Vereinfachung des Ausdrucks sin²(x) + cos²(x).

from sympy import * 
x=Symbol('x')
expr=sin(x)**2 + cos(x)**2 
simplify(expr)

Output:
1

3. Erweitern

        Expand() ist eine der häufigsten Vereinfachungsfunktionen in SymPy und wird zum Erweitern von Polynomausdrücken verwendet. Zum Beispiel -

a,b=symbols('a b') 
expand((a+b)**2)

expand((a+b)*(a-b))

        Die Funktion Expand() vergrößert normalerweise die Größe eines Ausdrucks, obwohl sie bei Anwendung gelegentlich die Größe eines Ausdrucks verringert. Im Allgemeinen kann der Aufruf von expand() zu größeren Ausdrücken führen, es gibt jedoch Ausnahmen, in denen diese vereinfacht werden.

expand((x + 1)*(x - 2) - (x - 1)*x)

Output:
-2

4. Faktorisierung

        Diese Funktion nimmt ein Polynom und zerlegt es über den Bereich der rationalen Zahlen in seine irreduziblen Komponenten.

x,y,z=symbols('x y z') 
expr=(x**2*z + 4*x*y*z + 4*y**2*z) 
factor(expr)

factor(x**2+2*x+1)

        Die Funktion Factor() ist die Umkehrung von Expand() und garantiert irreduzible Faktoren. Factor_list() bietet eine strukturierte Ausgabe von Faktoren.

expr=(x**2*z + 4*x*y*z + 4*y**2*z) 
factor_list(expr)

Output:
(1, [(z, 1), (x + 2*y, 2)])

5. Sammeln, sammeln

        Diese Funktion sammelt die additiven Komponenten eines Ausdrucks basierend auf einer Liste von Ausdrücken und berücksichtigt dabei rationale Exponenten.

expr=x*y + x - 3 + 2*x**2 - z*x**2 + x**3 
expr

6. Stornierung

        Der Zweck der Funktion cancel() besteht darin, jede rationale Funktion in die allgemeine Form p/q umzuwandeln, wobei p und q erweiterte Polynomausdrücke ohne gemeinsame Faktoren sind. Darüber hinaus sind die führenden Koeffizienten von p und q ganze Zahlen und weisen keinen Dezimalteil auf.

expr1=x**2+2*x+1 
expr2=x+1 
cancel(expr1/expr2)

Output:
x+1

expr = 1/x + (3*x/2 - 2)/(x - 4) 
expr

cancel(expr)

7. trigsimp ( trigonometrische Identität)

        Der Zweck dieser Funktion besteht darin, trigonometrische Identitäten zu vereinfachen. Es ist erwähnenswert, dass die Namenskonvention für inverse trigonometrische Funktionen das Hinzufügen von „a“ als Präfix zum Funktionsnamen beinhaltet. Arkuskosinus wird beispielsweise als „acos()“ dargestellt.

from sympy import trigsimp, sin, cos 
from sympy.abc import x, y
expr = 2*sin(x)**2 + 2*cos(x)**2 
trigsimp(expr)

Output:
2

        Die trigsimp-Funktion verwendet eine Heuristik, um die am besten passenden trigonometrischen Identitäten anzuwenden.

8. Vereinfachung exponentieller Terme

Diese Funktion vereinfacht den gegebenen Ausdruck durch die Kombination von Potenzen mit ähnlichen Basen und Exponenten.

expr=x**y*x**z*y**z 
expr

powsimp(expr)

        Sie können die Funktionsweise von powsimp() auf zwei Arten steuern: durch Kombination nur der Basen oder nur durch Kombination der Exponenten. Der Standardmodus „Alle“ kombiniert Basis und Exponent. Wenn Sie „force“ auf True setzen, werden die Basen unabhängig von den Annahmen zusammengeführt.

powsimp(expr, combine='base', force=True)

9. Combsimp

        Sie können die Combsimp()-Funktion von SymPy verwenden, um kombinatorische Ausdrücke mit Fakultäten und Binomialen zu vereinfachen. Darüber hinaus bietet SymPy auch eine dedizierte Factorial()-Funktion zur Verarbeitung von Fakultäten.

expr=factorial(x)/factorial(x - 3) 
expr

Um den obigen Kombinationsausdruck zu vereinfachen, verwenden wir die Funktion Combsimp() wie unten gezeigt −

combsimp(expr)

10. Logarithmische Kombination

Diese Funktion nimmt Logarithmen und kombiniert sie mithilfe der folgenden Regeln: −

• log(x) + log(y) == log(x*y), wenn beide positiv sind
• a*log(x) == log(x**a) wenn x positiv und a reell ist

logcombine(a*log(x) + log(y) - log(z))

Wenn der Parameter „Force“ in dieser Funktion aktiviert ist, geht sie davon aus, dass die oben genannten Bedingungen gültig sind, sofern keine Annahmen über die Menge vorliegen.

logcombine(a*log(x) + log(y) - log(z), force=True)

11. SymPy – Derivate

        Die Ableitung einer Funktion gibt an, wie schnell sich eine ihrer Variablen ändert. Dies entspricht der Bestimmung der Steigung der Tangente an einem bestimmten Punkt. In SymPy können Sie die Funktion „diff()“ verwenden, um das Differential eines mathematischen Ausdrucks mit Variablen zu berechnen.

diff(expr, variable)
from sympy import diff, sin, exp 
from sympy.abc import x,y 
expr=x*sin(x*x)+1 >>> expr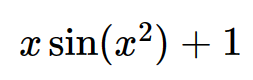

diff(expr,x)

diff(exp(x**2),x)

Um mehrere Ableitungen zu berechnen, wiederholen Sie einfach die Variablen für jeden Differenzierungsschritt oder geben Sie die gewünschte Reihenfolge an, indem Sie nach der Variablen einen numerischen Wert angeben.

diff(x**4,x,3)

Output:
24x

for i in range(1,4): print (diff(x**4,x,i))

Output:
4*x**3
12*x**2
24*x

        Sie können auch die diff()-Methode eines Ausdrucks aufrufen. Es funktioniert ähnlich wie die Funktion diff().

expr=x*sin(x*x)+1 
expr.diff(x)

        Mit der Derivative-Klasse in SymPy können Sie nicht ausgewertete Ableitungen erstellen und dabei dieselbe Syntax wie die Funktion diff() verwenden. Um das tatsächliche Ergebnis dieser Ableitung zu erhalten, können Sie die Doit-Methode anwenden.

from sympy import Derivative 
d=Derivative(expr) 
d

d.doit()

12. SymPy – Integration

        Im SymPy-Paket finden Sie das Integrationsmodul, das für die Berechnung bestimmter und unbestimmter Integrale mathematischer Ausdrücke konzipiert ist. Die Methode „integrate()“ kann primitive oder unbestimmte Integrale auswerten, wenn Variablen nach dem Ausdruck bereitgestellt werden.

integrate(f, x)

        Um das bestimmte Integral zu berechnen, übergeben Sie die Parameter wie folgt: −

(integration_variable, lower_limit, upper_limit)

from sympy import * 
x,y = symbols('x y') 
expr=x**2 + x + 1 
integrate(expr, x)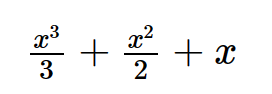

expr=sin(x)*tan(x) 
expr 
integrate(expr,x)

expr=exp(-x**2) 
integrate(expr,(x,0,oo) )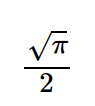

        Mit einem Integral-Objekt können Sie nicht berechnete Integrale erstellen, die durch Aufrufen der Methode doit() berechnet werden können.

expr = Integral(log(x)**2, x) 
expr

expr.doit()

13. Integrale Transformation

SymPy unterstützt verschiedene Arten von Integraltransformationen wie folgt:

• Laplace-Transformation
• Fourier-Transformation
• Sinustransformation
• Kosinustransformation
• Hankel-Transformation

Die genannten Funktionen befinden sich im Modul sympy.integrals.transforms. Es werden Beispiele bereitgestellt, die die Berechnung von Fourier-Transformationen und Laplace-Transformationen veranschaulichen.

Beispiel 1

from sympy import fourier_transform, exp 
from sympy.abc import x, k 
expr=exp(-x**2) 
fourier_transform(expr, x, k)

Wenn Sie den obigen Befehl in der Python-Shell ausführen, wird die folgende Ausgabe generiert:

sqrt(pi)*exp(-pi**2*k**2)

Dies entspricht -

Beispiel 2

from sympy.integrals import laplace_transform 
from sympy.abc import t, s, a 
laplace_transform(t**a, t, s)

Wenn Sie den obigen Befehl in der Python-Shell ausführen, wird die folgende Ausgabe generiert:

(s**(-a)*gamma(a + 1)/s, 0, re(a) > -1)

14. SymPy – Matrix

        In der Mathematik ist eine Matrix eine strukturierte Anordnung von Elementen, die Zahlen, Symbole oder mathematische Ausdrücke enthalten können. Das Konzept der Matrixoperationen umfasst die Durchführung verschiedener mathematischer Operationen an diesen Matrixstrukturen, die alle spezifischen mathematischen Richtlinien folgen.

        Eine bemerkenswerte Anwendung von Matrizen liegt im Bereich der linearen Transformationen, einem wichtigen Konzept in vielen wissenschaftlichen Disziplinen, insbesondere im Bereich der Physik, wo matrizenbasierte Methoden weit verbreitet sind.

        Im SymPy-Paket gibt es ein eigenes Modul zur Verarbeitung von Matrizen. Dieses Modul stellt die Matrix-Klasse vor, eine Grundkomponente, die als Darstellung einer Matrix dient und Matrixoperationen erleichtert.

from sympy.matrices import Matrix

from sympy.matrices import Matrix 
m=Matrix([[1,2,3],[2,3,1]]) 
m

        Matrizen werden aus Listenobjekten geeigneter Größe erstellt. Sie können eine Matrix auch erhalten, indem Sie Listenelemente über eine angegebene Anzahl von Zeilen und Spalten verteilen.

M=Matrix(2,3,[10,40,30,2,6,9]) 
M

Eine Matrix ist ein veränderliches Objekt. Das Matrixmodul stellt außerdem die Klasse ImmutableMatrix bereit, um unveränderliche Matrizen zu erhalten.

15. Grundlegende Steuerung

Die Shape-Eigenschaft eines Matrix-Objekts gibt seine Größe zurück.

M.shape

Output:
(2,3)

Die Methoden row() und col() geben eine angegebene Anzahl von Zeilen bzw. Spalten zurück.

M.row(0)

Output:
[10 40 30]

M.col(1)

Verwenden Sie den Slicing-Operator von Python, um ein oder mehrere Elemente abzurufen, die zu einer Zeile oder Spalte gehören.

M.row(1)[1:3]

Output:
[6, 9]

Die Matrixklasse verfügt über die Methoden row_del() und col_del(), um bestimmte Zeilen/Spalten aus der angegebenen Matrix zu löschen

M=Matrix(2,3,[10,40,30,2,6,9]) 
M.col_del(1) 
M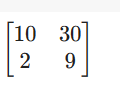

Mit dem folgenden Befehl können Sie Stile auf die Ausgabe anwenden:

M.row_del(0) 
M

Output:
[2  6  9]

In ähnlicher Weise fügen die Methoden row_insert() und col_insert() eine Zeile oder Spalte an einem angegebenen Zeilen- oder Spaltenindex hinzu

M1=Matrix([[10,30]]) 
M=M.row_insert(0,M1)
M

16. Arithmetische Operationen

        Definieren Sie allgemeine Operatoren +, - und *, um Addition, Subtraktion und Multiplikation durchzuführen.

M1=Matrix([[1,2,3],[3,2,1]]) 
M2=Matrix([[4,5,6],[6,5,4]]) 
M1+M2

M1-M2

        Eine Matrixmultiplikation kann auftreten, wenn die Anzahl der Spalten in der ersten Matrix mit der Anzahl der Zeilen in der zweiten Matrix übereinstimmt. Darüber hinaus hat das Ergebnis die gleiche Anzahl an Zeilen wie die erste Matrix und die gleiche Anzahl an Spalten wie die zweite Matrix.

M1=Matrix([[1,2,3],[3,2,1]]) 
M2=Matrix([[4,5],[6,6],[5,4]]) 
M1*M2

17. Matrixkonstruktor

        SymPy bietet verschiedene spezialisierte Matrixklassen, wie z. B. Identitätsmatrizen und All-Null- oder vollständig gefüllte Matrizen. Diese Klassen werden durch die Namen „Auge“, „Nullen“ bzw. „Einsen“ repräsentiert. Konkret ist die Identitätsmatrix eine quadratische Matrix, in der alle Elemente entlang der Diagonale gleich 1 sind und alle anderen Elemente auf 0 gesetzt sind.

from sympy.matrices import eye
eye(3)

        In einer Diagonalmatrix werden die Elemente auf der Diagonale entsprechend den bereitgestellten Parametern initialisiert.

from sympy.matrices import diag 
diag(1,2,3)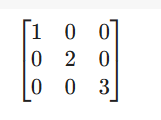

        Alle Elemente in der Nullmatrix werden auf 0 initialisiert.

from sympy.matrices import zeros 
zeros(2,3)

        Ebenso sind Einsen eine Matrix, bei der alle Elemente auf 1 gesetzt sind.

from sympy.matrices import ones
ones(2,3)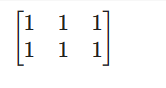

        So weit, ist es gut. Wir haben mit dieser Bibliothek verschiedene Vereinfachungen gesehen, und die Mathe-Toolbox ist auf jeden Fall gut. In den nächsten Abschnitten erfahren Sie, wie Sie Funktionen definieren und verwenden, die im Wesentlichen die Bausteine ​​der Simulation bilden.